В этом случае воспроизведение случайных факторов реализуется с помощью специальных алгоритмов, что обеспечивает получение периодических детерминированных числовых последовательностей с большим периодом. Такие последовательности похожи на настоящие случайные и называются псевдослучайными или квазислучайными. Алгоритм получения периодической последовательности целых псевдослучайных чисел записывается следующим образом:
где Z[…] - остаток от деления целых чисел (например, Z [ 15 / 6 ]= 3), i = 1, 2,…... Здесь a и b - целые числа, при этом a < b. Например, если выбрать а = 7, b = 17, g0 =3, то получим следующую псевдослучайную последовательность чисел: 3, 4, 11, 9, 12, 16, 10, 2, 14, 13, 6, 8, 5, 17, 15, 3, 4, 11, 9,…. В этом случае период случайной последовательности равен 16, т.е. алгоритм позволяет получить последовательность из 16 целых чисел, каждое число в данной последовательности "условно" равновероятно принимает значение из интервала от 1 до 16. Такой алгоритм фактически имитирует случайную величину.
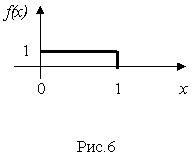
Практически во всех средах программирования присутствуют датчики случайных чисел, реализованные по алгоритмам, близким к приведенному ранее. Так, например, в среде Borland C++ есть функция int random (int n), которая (при обращении к ней) выдает случайное целое число из интервала от 0 до n-1. Таким образом, написав в тексте программы строку a = random (1000), мы получим значение (реализацию) случайной величины, которое будет присвоено переменной а. На рис.5 приведена программа, которая формирует массив из 10 случайных целых чисел, равновероятно принимающих значение из интервала от 0 до 999, и выводит их на экран. В большинстве ситуаций, связанных с моделированием, в качестве исходного (или базового) для дальнейших преобразований требуется датчик случайных чисел с равномерной плотностью распределения вероятности из интервала от 0 до 1. График плотности распределения таких случайных чисел показан на рис.6.
Очевидно, что если для получения случайного числа х воспользоваться функцией random в следующем варианте х = random (N)/(float)N , то при N>>1 (реально N порядка 10000) мы получим случайное число х с плотностью распределения вероятности, показанной на рис.6. На рис.7 приведена программа формирования массива случайных чисел с плотностью распределения вероятности f(х) = 1 при 
.
Используя датчик случайной величины X с равномерным распределением в интервале от 0 до 1, с помощью очевидного преобразования можно получить случайную величину у с равномерным распределением в интервале от а до с:
.Рассмотрим теперь вопрос об экспериментальной оценке плотности распределения вероятности. Всегда есть неуверенность в том, что тот или иной алгоритм выдает случайные числа с требуемой плотностью распределения вероятности. Таким образом, задача заключается в экспериментальном исследовании f(х). Считаем, что случайное число х попадает в некоторый диапазон, например 
, который мы, как правило, всегда знаем. Далее разбиваем этот интервал на N отрезков длиной 
. Обращаясь к датчику случайной величины М раз, мы можем получить оценку вероятности попадания случайного числа в n-й отрезок 
, где Mn - число экспериментов, в результате которых величина х попала в n-й отрезок. Для пересчета вероятности попадания случайной величины в плотность распределения вероятности f(n) необходимо поделить Р(n) на d. При увеличении N, M и большом отношении M/N мы получим экспериментальную оценку плотности распределения вероятности, близкую к истинной. Далее приведено формальное описание алгоритма.
Инициализируем массив P(n) = 0, где n изменяется в интервале от 0 до N-1 включитльно.
| Цикл по m от 0 до M-1 (это цикл по экспериментам) | |
| x = sl_vel | (обращение к датчику случайной величины); |
| n = целая часть [N(x-a)/(b-a )] | (вычисление номера отрезка n, в который попало значение случайной величины); |
| P(n) = P(n) + 1 | ( при попадании числа х в n - й отрезок добавляем единицу в элемент массива P(n)). |
| Завершение цикла по m | |
Теперь для получения оценки плотности распределения вероятности f(n) необходимо поделить P(n) на M, а затем на d. Это выполняется в следующем цикле.
| Цикл по n от 0 до N-1 (это цикл по отрезкам) |
| f(n) = [P(n) /M]/ d |
| Завершение цикла по n |
Описанная ранее методика статистической оценки плотности распределения вероятности выполнена в соответствии с общим методом моделирования Монте-Карло. Суть данного метода заключается в том, что для вычисления площади сложной фигуры необходимо случайно и равномерно формировать в прямоугольнике, окружающем фигуру, точки. Количество точек, попавших в эту фигуру, обозначим 
, общее же количество "разбросанных" точек обозначим M. В этом случае при стремлении M к бесконечности отношение площади фигуры к площади прямоугольника ( в котором равномерно разбрасываются точки ) равно отношению / М.