1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

1.2.Метод локализации [1,2]

Алгоритм метода:

1. 1.Интервал поиска минимума (a,b) разбивается на четыре равные части (подыинтервалы) точками Х1, Х2 и X3 (рис.3).

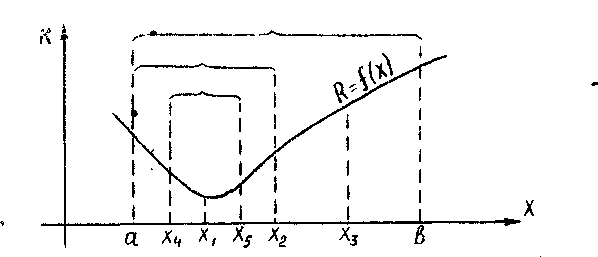
Рис. 3.

2. Вычисляются значения целевой функции R=f(x) во всех точках разбиения и в точках x=a, x=b.
3. Полученные значения f(x) сравниваются между собой, и из них выбирается наименьшее.
4. Локализуют минимум, причем новый интервал поиска равен двум старым подынтервалам с наименьшим значением f(x) на их общей границе (на рис.3 это соответствует интервалу (a,x₂)).
5. Делят интервал, в котором локализован минимум, опять на четыре равных подынтервала (на рис.3 точками x₄, x₅ ) и снова вычисляют значения критерия оптимальности в точках деления, сравнивают их между собой, находят наименьшее, локализуют минимум в меньшем интервале (на рис.3 в интервале (x₄, x₅)) и так далее до тех пор, пока минимум не будет локализован в интервале, размер которого соответствует заданной точности поиска.

Замечание. Интервал поиска разбивается именно на четыре подынтервала с целью уменьшения объема вычислений: при этом каждый последующий подынтервал делится пополам, и вычислять значение функции нужно только в двух новых точках, так как её значения на концах нового интервала и в его середине известны из предыдущих расчетов.

Длина интервала неопределенности после S вычислений значений целевой функции определяется выражением:

(4)

абсолютная ошибка в нахождении минимума составляет:

(5)

Пример.

Найти минимум целевой функции:

в области 0≤x≤2, локализовав его на отрезке длиной не более 0,3.

Решение.

Первый шаг.

Разбиваем интервал поиска 0≤x≤2 на четыре равные, части и вычисляем значения функции f(x) на концах интервала и в точках разбиения:

a=0 f(a)=0

x₁=0,5 f(x₁)=-9,16

x₂=1,0 f(x₂)=-11,7

x₃=1,5 f(x₃)=11,32

b=2 f(b)=90,0

Минимальное значение целевой функции есть f(x₂)=f(1,0)=-17,5 .Интервал поиска уменьшаем, ограничивая точками x₁= 0,5, x₃ =1,5, т.е. локализуем экстремум в области 0,5≤x≤1,5.

Второй шаг.

Новый интервал поиска 0,5≤x≤1,5 разбиваем на четыре равные части и вычисляем значения целевой функции в точках разбиения и на концах интервала.

Значения функции

f(0,5)=-9,16;

f(1,0)=-11,67;

f(1,5)=11,32

вычислены ранее на предыдущем этапе, поэтому вычисляем лишь

f(0,75)=-12,12

f(1,25)=-5,02

Выбираем минимальное значение f(x):

f(0,75)=-12,12

и интервал поиска вновь уменьшаем, т.е. локализуем экстремум в области 0,5≤x≤1.

Третий шаг.

Новый интервал поиска 0,5≤x≤1 разбиваем на четыре равные части.

Значения

f(0,5)=-9,16;

f(0,75)=-12,12;

f(1)=11,67

вычислены на втором этапе, поэтому вычисляем только

f(0,625)=-10,93;

f(0,875)=-12,48

Из всех значений функции выбираем минимальное f(0,875)=-12,48 и локализуем экстремум в области 0,75≤x≤1.

Расчет окончен, т.к. экстремум локализован в области Δx = 0,25< 0,3 с точность Δ=0,125.

Ответ: x_min=0.875 ± 0,125; f(0,875) =-12.48.