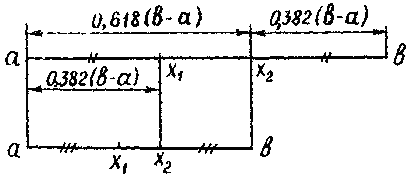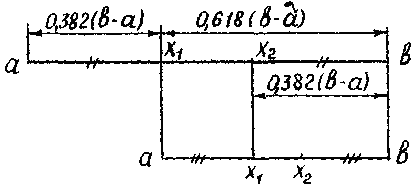1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

1.3. Метод золотого сечения [1-7]

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения.

Если известно, что функция f(x) унимодальная на отрезке [a,b], то положение точки минимума можно уточнить, вычислив f(x) в двух внутренних точках отрезка. При этом возможны две ситуации:

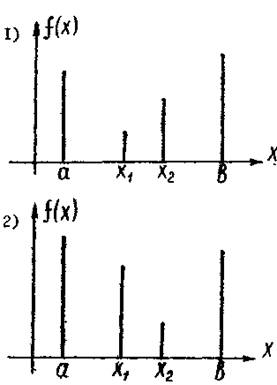
	f(x1)<f(x2) Минимум реализуется на отрезке [a, x2].
	f(x1)>f(x2) Минимум реализуется на отрезке [x1, b].

Рис. 4.

В методе золотого сечения каждая из точек x₁ и x₂ делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т.е. равно так называемому "золотому отношению". Это соответствует следующему простому геометрическому представлению:

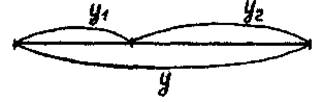
Здесь

или

(6)

Обозначив

получаем

откуда

Итак, длины отрезков [a,x₁] и [x₂,b] одинаковы и составляют 0,382 от длины (a,b). Значениям f(x₁) и f(x₂) определяется новей интервал (a,x₂) или (x₁,b) , в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления совпадает с уже использованной на предыдущем шаге.

Взаимное расположение точек первых трех вычислений можно показать следующим образом:

1) f(x₁)<f(x₂)

Первый шаг
Второй шаг

2) f(x₁)≥f(x₂)

Первый шаг
Второй шаг

Рис. 5

Таким образом, длина интервала неопределенности на каждом шаге сжимается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем - одно.

Длина интервала неопределенности после S вычислений значений f(x) составляет:

(7)

Алгоритм метода золотого сечения для минимизации функции f(x) складывается из следующих этапов:

1. Вычисляется значение функции f(x₁), где x₁=a+0,382(b-a).
2. Вычисляется значение функции f(x₂), где x₁=b+0,382(b-a).
3. Определяется новый интервал (a,x2) или (x1,b), в котором локализован минимум.
4. Внутри полученного интервала находится новая точка (x₁ в случае 1) или (x₂ в случае 2), отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f(x). Затем вычисления повторяются, начиная с пункта 3, до тех пор, пока величина интервала неопределенности станет меньше или равна ε, где ε - заданное сколь угодно малое положительное число.

Блок-схема алгоритма поиска минимума функции f(x) методом золотого сечения.

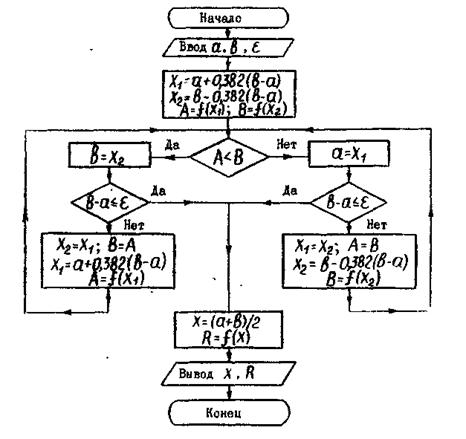
Рис. 6.

Пример.

Используя метод золотого сечения, минимизировать функцию f(х)=x²+2х на интервале (-3,5). Алина конечного интервала неопределенности не должна превосходить 0,2.

Решение.

Первый шаг. a=-3, b = 5, b-a = 8.

x₁= -3 + 0,362∙8 = 0,056;

x₂ = 5 - 0,382∙8 = 1,944;

f(x₁)= 0,056² +2∙0,056 =0,115;

f(x₂)= I,944² + 2∙1,944=7,667;

f(x₁)<f(x₂). Новый отрезок [-3; 1,944].

Второй шаг. a=-3, b = 1,944, b-a =4,944.

x₁ = -3+ 0,382∙4,944 = -1.112;

x₂= 0,056;

f(x₁)= (-1,112)² + 2∙(-1,112) = -0.987;

f(x₂)=0,115;

f(x₁)<f(x₂). Новый отрезок [-3; 0,056].

Дальнейшие вычисления оформим в виде таблицы. Значения функции f(x₂), вычисленные на каждом шаге, помечены звездочкой.

Таблица 1
№ шага	a	b	b-a	x1	x2	f(x1)	f(x2)
1	-3,000	5,000	8,000	0,056	1,944	0,115^*	7,667^*
2	-3,000	1,944	4,944	-1,112	0,056	-0,987^*	0,115
3	-3,000	0,056	3,056	-1,832	-1,112	-0,308^*	-0,987
4	-1,832	0,056	1,888	-1,112	-0,664	-0,987	-0,887^*
5	-1,832	-0,664	1,168	-1,384	-1,112	-0,853^*	-0,987
6	-1,384	-0,664	0,720	-1,112	-0,936	-0,987	-0,996^*
7	-1,384	-0,936	0,448	-1,208	-1,112	-0,957^*	-0,987
8	-1,208	-0,936	0,272	-1,112	-1,032	-0,987	-0,999^*
9	-1,112	-0,936	0,176

После восьми шагов, содержащих девять вычислений функции, интервал неопределенности равен (-1,112; -0,936), его длина 0,176 <0,2. В качестве точки минимума может быть взята середина этого интервала -1,024; при этом f(-1,024)=-0,999. Заметим, что точкой точного минимума является -1,0; f(-1,0)=-1.