2. МНОГОМЕРНЫЙ ПОИСК.

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ [l,2,6 - 8]

 

2.3.1. Безградиентные методы. Покоординатный спуск

Наиболее простым способом определения направления спуска является выбор в качестве  одного из координатных векторов . Это позволяет поочередно изменять все независимые переменные x1, x2,…, xn так, чтобы на каждой из них достигалось наименьшее значение целевой функции. Очеред­ность варьирования независимых переменных при этом устанавлива­ется произвольно и не меняется в процессе поиска. В результате многомерный поиск заменяется последовательностью одномерных по­исков с любой стратегией минимизации функции одной переменной (см. методы, описанные выше).

Данный метод эффективен в случае единственного минимума функции. Для уменьшения числа вычислений величину шага λ меняют при каждом переходе от поиска минимума по одной перемен­ной к поиску минимума по другой переменной.

Алгоритм метода может быть представлен следующими этапами.

1. Задают исходную точку поиска .

2. Определяют направление поиска; если варьируется переменная x1, то    .

3. Делают первый шаг в направлении . Значение λ1, выбирают способом удвоения или минимизацией функции  по λ1. Если ана­литическое выражение целевой функции достаточно простое, для выбора  можно использовать условие:

4. После определения положения минимума по координате x1 дела­ют шаг в направлении : . Значение λ2, находят, минимизируя функцию  по λ2 и так далее.

5. Поиск заканчивают при выполнении условия:

(15)

Пример

Пусть целевая функция имеет вид

Требуется найти её минимум с точностью ε = 0,01.

Решение.

1. Примем в качестве исходной точку А0 (2,1). Значение целевой функции в этой  точке f(А0) = 7.

2. Направление поиска выберем параллельно координатной оси OX1, .

3. Изменим переменную x1.

    Значение  найдём из условия:

    f(x1+λ1e1, x2)=2(x1+λ1e1)2+x22-( x1+λ1e1)∙x2,

   =4(x1+ λ1e1)e1-x2e1=0λ1=0,25x2-x1,

 

 

Тогда .

Итак, нашли точку A1(0,25; 1), в которой значение целевой функции f(A1) = 0,875.

 

4. Изменим переменную x2.

   Значение , найдем из условия:

     f(x1, x2+λ2e2)=2 x12 +(x2+λ2e2)2 -x1( x2+λ2e2),

   =2(x2+ λ2e2)e2-x1e2=0λ2=0,5x1-x2,

  

Тогда .

Нашли точку A2(0,25;0,I25), f(A2) = 0,109.

 

5. От точки А2 вновь изменим направление поиска и сведём даль­нейшие   вычисления в таблицу 4.

 

Таблица 4

Номер

итерации k

λ

x1

x2

f(x1,x2)

0

 

 

2

1

7

1

1,0

-1,750

0,250

1,000

0,875

2

0,1

-0,875

0,250

0,125

0,109

3

1,0

-0,215

0,030

0,125

0,013

4

0,1

-1,108

0,030

0,015

0,001

 

После четвёртой итерации выполняется условие окончания поиска:

Ответ: минимум целевой функции находится в точке (0,030; 0,015), f(Amln)= 0,001.

Отметим, что точный минимум целевой функции находится в точке (0,0), f( 0.0 ) = 0.

Рассмотрим на другом примере покоординатный спуск с ис­пользованием для выбора величины шага способа удвоения. Соот­ветствующая блок-схема представлена на рис.9.

Пусть требуется минимизировать функцию f(x1,x2)= 4(x1 - 5)2 + (x2 - 6)2, начиная из точки А0(8,9);  f (A0)=45.

1.  Изменим переменную . Найдём , применяя способ удвоения.

    Выберем произвольное значение = -0,5.

    Тогда =8+(-0,5)∙1=7,5;  f(7,5; 9)=34<f(8;9)

    Удвоим шаг: = -1.

    При этом =8+(-1)∙1=7;  f(7; 9)=25<f(7,5;9).

    Ещё раз удвоим шаг: =-2.

    Тогда =8+(-2)∙1=6;  f(6; 9)=13<f(7;9).

    Уменьшение целевой функции позволяет ещё удвоить шаг: =-4.

    При этом  =8+(-4)∙1=4;  f(4; 9)=13.

    Функция не уменьшилась. Следовательно, наилучшее значение = -2. Точка   A1, найденная с этим значением , имеет координаты =6; =9; f(A1)=13.

Рис. 9. Блок – схема покоординатного спуска с удвоением шага

 

2.  Ещё раз изменим переменную x1:  

     Примем  ==-2.

     Тогда   =6+(-2)∙1 = 4;  f(4;9)=13.

     Функция не уменьшилась. Уменьшим шаг вдвое: =-1.

     При этом = 6 + (-1)∙1 = 5; f(5;9)=f(A2)=9<f(A1).

3. Сделаем шаг по переменной x2:  

     Примем  ==-1.

     Тогда   =9+(-1)∙1 = 8; f(5;8)=f(A3)=4<f(A2).

4. Ещё раз изменим переменную x2: ,

    где  ==-2

    Тогда   =8+(-1)∙1 = 7; f(5;7)=f(A4)=1<f(A3).

5. Ещё раз изменим переменную x2 с тем же значением λ:

     =7+(-1)∙1 = 6; f(5;6)=f(A5)=0<f(A4).

6. Следующий шаг по x2 с тем же параметром λ приводит к воз­растанию   функции:

 =6+(-1)∙1 = 5; f(5;5)=1.

    Следовательно, точка A5(5;6) является точкой минимума целевой функции.

На рис. 10 показана траектория поиска.

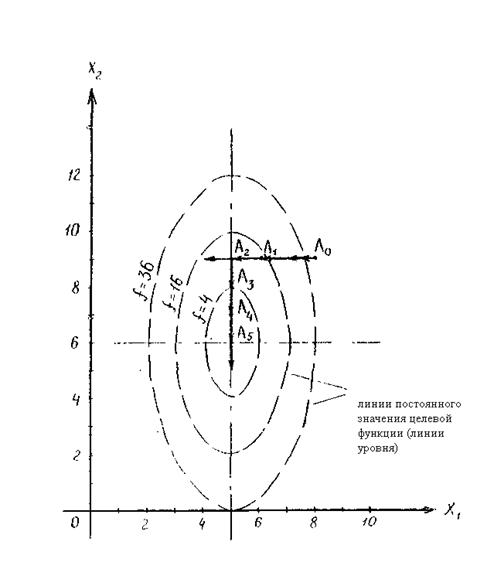
Рис. 10