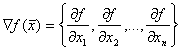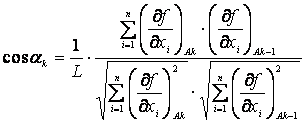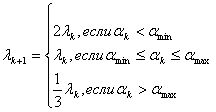2. МНОГОМЕРНЫЙ ПОИСК.

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ [l,2,6 - 8]

2.3.2. Градиентные методы

Градиентные методы связаны с поиском по направлению градиента или антиградиента оптимизируемой функции. Градиент функции обозначается и определяется как вектор-столбец из первых частных производных этой функции:

(16)

В каждой точке градиент ортогонален линии уровня f(x₁, x₂,…, x_n)=const , проходящей через эту точку, и направлен в сторону наискорейшего возрастания функции.

Вектор-антиградиент также ортогонален линии уровня, проходящей через данную точку, но направлен в сторону наискорейшего убывания функции. Таким образом, вектор, указывающий направление поиска при минимизации функции , есть .

Процедура вычисления производных целевой функции весьма трудоёмка. На практике их часто приходится вычислять, приближенно, пользуясь разностными соотношениями. Например, для функции двух переменных разностные формулы имеют вид:

	(17а)
	(17б)

где Δx₁, Δx₂ - некоторые малые приращения аргументов.

Величины Δxi выбираются так, чтобы ошибка аппроксимации производной не превышала разумного уровня.

В общем случае при отыскании минимума целевой пункции схема перехода из точки в точку, определяется не просто антиградиентом, а произведением антиградиента на смметричную, положительно определенную матрицу H_k. Алгоритм метода при этом имеет вид:

(18)

Числа λ_k выбираются согласно 2.2. В частности, можно для определения λ на (k+1)-ом шаге использовать косинус угла α_k между последовательными векторами переходов в процессе спуска от точки A_k+1 до А_k:

(19)

Тогда

(20)

В качестве α_min и α_max можно принять, например, углы в 30° и 90°, соответственно.

Модификации градиентных методов.

В зависимости от выбора матриц Н_k градиентные методы делятся на метод наискорейшего спуска, метод изменения масштабов, метод сопряженных направлений, метод Ньютона, метод Давидона-Флетчера-Пауэлла и другие. Рассмотрим две модификации - наискорейший спуск и метод сопряженных направлений.