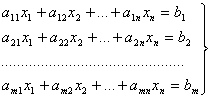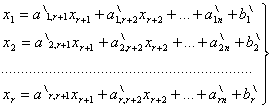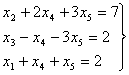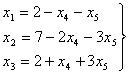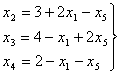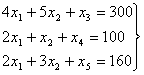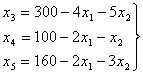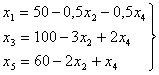4. МНОГОМЕРНЫЙ ПОИСК.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ [l,2]

4.3. Симплексный метод решения задач линейного программирования

Симплексный метод реализует идею последовательного улучшения решения, jto универсальный метод, который может быть применен при решении любой задачи линейного программирования.

Задача.

Найти решение системы уравнений:

(41)

удовлетворяющее условиям неотрицательности

X1≥0, X2≥0, …, Xn≥0

(42)

и максимизирующее линейную функцию

R=C1X1+C2X2+…+CnXn

(43)

Полагая, что ранг r матрицы коэффициентов меньше числа неизвестных, выразим r неизвестных системы (41) через остальные

(44)

В системе (44) число линейно независимых уравнений равно r.

Неизвестные X₁ , Х₂> ,...,Х_r назовем базисными, остальные неизвестные назовем свободными.

Так как свободным неизвестным можно придавать любые неотрицательные значения ( Х_r+1 ≥0, Х_r+2≥0 ,..., Х_п≥ 0 ), то свободные члены b₁^\, b₂^\ ,..,b_r^\ должны быть неотрицательными (b_i^\≥0 при i=1,2,…,r). В противном случае (т.е. если b_i<0 для i=1,2,…r) при Х_r+1=0, X_r+2=0,..., Х_n =0 получим X₁<0, Х₂< 0,..., Х_r<0, что недопустимо по условию задачи.

Положим все свободные неизвестные равными нулю: Х_r+1=0, X_r+2=0,..., Х_n =0. Получим:

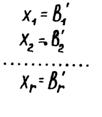
Полученное решение системы является допустимым, т.к удовлетворяет условиям (41) и (42), и называется базисным решением. При этом вектор (b₁^\, b₂^\,…, b_r^\, 0,…,0) называется базисным вектором.

Подставим в оптимизируемую линейную функцию (43) найденные базисные неизвестные, выраженные через свободные неизвестные. Для первого базисного решения все свободные неизвестные X_r+1=0, поэтому получим R=С_о^\.

Далее переходим к другому базисному решению. При этом значение оптимизируемой линейной функции R должно увеличиваться (если ищем максимум R ) или уменьшаться (если ищем минимум R).

Переход осуществляется следующим образом: одна из базисных переменных заменяется другой, которая ранее была свободной, и т. д. Этот процесс повторяется до тех пор, пока R не достигнет экстремального значения.

Рассмотрим принцип нахождения решения задачи линейного программирования на примерах.

Пример 1.

Найти решение системы уравнений:

(45)

удовлетворяющее условиям неотрицательности:

X1≥0, X2≥0, …, X5≥0

(46)

и минимизирующее целевую функцию:

R=3-X4+X5

(47)

Выразим базисные переменные X₁, Х₂, X₃ через свободные X₄ и X₅:

(48)

Приняв свободные переменные X₄ и X₅ равными нулю, получим первое базисное решение, т.е. выполним первую итерацию симплексных преобразований:

Х1= 2, Х2 = 7, Х3= 2, Х4 =0, Х5= 0

(49)

При этом R = 3.

Выполним вторую итерацию, которая приведет к уменьшению R.

Анализ уравнения (47), которое определяет R, показывает, что целевая функция R может быть уменьшена за счет уменьшения X₅ и увеличения X₄. Однако уменьшить Х₅ нельзя, т.к. на первой итерации Х₅= 0, а условие неотрицательности не позволяет сделать Х₅<0.

Значит, путь уменьшения R состоит в увеличении Х₄.

Увеличение Х₄ должно идти до тех пор, пока одна из переменных X_i , которая зависит от Х₄, не станет равной нулю и, следовательно, дальнейшее увеличение Х₄ приведет к отрицательному значению X_i, что недопустимо.

Из системы (48) следует, что Х₄ не может превышать значения 2, т.к. при Х₄>2 Х₁ становится меньше нуля (первое уравнение системы (48)), что недопустимо по условию задачи.

Принимаем Х₄=2, при этом Х₁=0. Подставим эти значения в систему уравнений (48), получим новое базисное решение:

Х1= 0, Х2 = 3, Х3= 4, Х4 =2, Х5= 0

(50)

При этом R=1.

Выразим новые базисные переменные Х₂, X₃, X₃ через свободные X₁ и X₅:

(51)

Подставим полученное выражение для Х₄ в выражение для целевой функции (47), получим:

R=1+X₁+2X₅.

Поскольку требуется получить минимум функции R, а уже на второй итерации X₁ и Х₅ равны нулю, то, учитывая, что X₁ и Х₅ не могут быть отрицательными, а любое увеличение X₁ и Х₅ не приводит к уменьшению R , делаем вывод: задача решена, и искомое решение есть результат второй итерации (50).

Пример 2.

Найти значения X_i, i=1,2,3,4,5, которые удовлетворяют системе уравнений:

(52)

условиям неотрицательности:

Xi , i = 1,2,3,4,5

(53)

к обеспечивают наименьшее значение целевой функции:

P=-10X1 - 12X2

(54)

Примем переменные Х₃, Х₄, Х₅ в качестве базисных и выразим их через свободные переменные X₁ и Х₂ из уравнений (52). Получим:

(55)

Первое базисное решение примет вид:

Х1= 0, Х2 = 0, Х3= 300, Х4 =100, Х5= 160

(56)

При этом R=0.

Из уравнения (54) видно, что целевая функция может быть уменьшена путем увеличения X₁ и Х₂ . Увеличим сначала X₁. Из (55) следует, что X₁ можно увеличить до значения X₁= 50, поскольку при большем его значении переменная Х₄ станет отрицательной.

Полагая X₁ =50, Х₂ = 0, из (55) получаем второе базисное решение:

Х1= 50, Х2 = 0, Х3= 100, Х4 =0, Х5= 60

(57)

При этом R=-500.

Примем ненулевые переменные в (57) X₁, X₃,X₅ в качестве базисных, а нулевые переменные Х₂, Х₄ в качестве свободных. Из системы (52) найдем:

(58)

Выражение для целевой функции (54) запишем через свободные параметры, заменив X₁ с помощью (58). Получим:

R=-500-7X2+5X4

(59)

Отсюда следует, что значение целевой функции можно изменить за счет увеличения Х₂, поскольку коэффициент при этой переменной в (59) отрицательный.

Максимальное значение Х₂ определяется соотношениями (58) и составляет Х₂ = 30. Из (58) при X₂=30, Х₄= 0 получаем третье базисное решение:

Х1= 35, Х2 = 30, Х3= 10 Х4 =0, Х5= 0

(60)

При этом R=-710.

Для проведения следующего шага симплексных преобразований ненулевые переменные в (60), т.е. X₁, Х₂, X₃, нужно принять в качестве базисных) а нулевые переменные Х₄, Х₅ - в качестве свободных. В этом случае целевую функцию можно записать в виде:

R = -710 +1,5X2 + 3,5Х5

(61)

Поскольку коэффициенты при Х₄, Х₅ положительные, то при увеличении этих параметров целевая функция возрастает. Следовательно, решение (60) является оптимальным.