3.1. Метод Эйлера

Пусть дано дифференциальное уравнение y′ = f(x,y) (1), с начальными условиями y(x₀) = y₀. Пусть y = y(x) – искомое точное решение. Интегральная кривая проходит через точку (x₀;y₀).

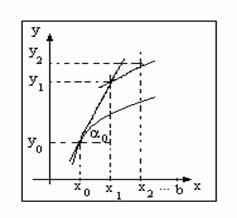
Найдем приближенные значения функции в точках x₁, x₂, ..., x _n. Построим систему равноотстоящих точек x₀, x₁ = x₀ + h, x₂ = x₁ + h, ... x_n = b. Проведем прямые x = x₀, x = x₁, ..., x = b. Рассмотрим отрезок [x₀; x₁]. На этом отрезке есть одна точка, которая принадлежит искомой кривой – это точка A(x₀; y₀). Заменим дугу искомой кривой y = y(x) на отрезке [x₀; x₁] касательной к ней, проведенной в точке (x₀; y₀). В качестве y₁ возьмем ординату точки пересечения прямой x = x₁ с касательной.

Очевидно y₁ = y₀ + h · tgα₀. Но tgα₀ = y′(x₀), т.е. y₁=y₀ + h · y′(x₀). Но из уравнения (1) следует, что y′(x₀) = f(x₀; y₀).

Итак, получаем y₁ = y₀ + h · f(x₀; y₀), x₁ = x₀ + h.

Предположим теперь, что точка (x_1; y₁) принадлежит искомой кривой. В этой точке опять проведем касательную к графику функции до пересечения с прямой x = x₂.

Тогда аналогично:

y₂ = y₁ + h · f(x₁; y₁);

x₂ = x₁ + h.

Продолжая и так далее, получим систему значений y₁, y₂, ..., y_n, которые и будут приближенными значениями функции y=y(x) в точках x₁, x₂, ..., x _n. Итак, расчетные формулы метода Эйлера:

y_m+1 = y_m + h ∙ f (x_m; y_m);

x_m+1 = x_m+ h.

Для системы дифференциальных уравнений

y′_i = f_i (x, y₁, y₂, ...y_k)

y_i(x₀) = y_i⁰ i =1,..., k.

расчетные формулы записываются аналогично:

y_i^m+1 = y_i^m + h · f_i (x, y₁^m, y₂^m,...y_k^m);

x_m+1 = x_m + h,

здесь i – номер уравнения в системе, n – номер шага.

Метод Эйлера является грубым методом, ошибка, которую мы допускаем на каждом шаге пропорциональна h, т.е. |y(x _k)-y _k|~h. Чтобы повысить точность вычислений, используют некоторые усовершенствованные методы.