3.2. Метод Эйлера-Коши

Пусть опять решаем уравнение y' = f(x,y), y(x₀) = y₀. Решение ищем на отрезке [x₀, x_n].

Пусть нам известны координаты некоторой точки, принадлежащей искомому решению (x_m; y_m). Найдем средний тангенс угла наклона касательной для двух точек: (x_m, y_m) и (x_m + h, y_m + h · ỹ_m).

Последняя точка, есть та самая, которую в методе Эйлера мы обозначаем (x_m+1; y_m+1), но здесь точка будет вспомогательной.

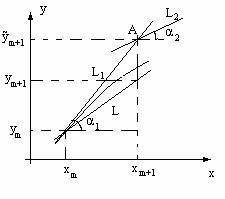
Итак, сначала по методу Эйлера находится точка А, лежащая на прямой L₁,тангенс угла наклона которой tg α ₁ = f(x_m; y_m). В этой точке снова вычисляется тангенс угла наклона касательной L₂

tg α₂ = f (x_m+ h; y_m + h · ỹ_m).

Затем через точку (x_m; y_m) проводим прямую L, тангенс угла наклона которой равен (tg α₁ + tg α₂)/2. Точка, в которой L пересечется с прямой x = x_m+1, и будет искомой (x_m+1; y_m+1).Таким образом, y_m+1 искомое приближение значения функции на данном шаге интегрирования.

Расчетные формулы метода Эйлера - Коши следующие:

ỹ_m+1 = y_m + h · f(x_m; y_m);

y_m+1 = y_m + (h/2) · [f(x_m; y_m) + f(x_m+1; ỹ_m+1)];

x_m+1 = x_m + h.

Аналогично, для системы дифференциальных уравнений:

y'_i = f_i(x, y₁, y₂, ... y_k), y_i = y_i⁰, i = 1, 2,... k;

ỹ_i^m+1 = y_i^m + h · f_i(x_m, y₁^m; y₂^m, ... y_k^m);

y_i^m+1 = y_i^m + (h/2)*[f_i(x_m, y₁^m, y₂^m, ... y_k^m) + f_i(x_m+1,ỹ₁^m+1, ỹ₂^m+1, ... ỹ_k^m+1);

x_m+1 = x_m + h.

Здесь i – номер уравнения системы, m – номер шага.