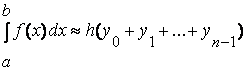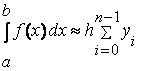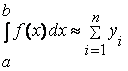1. 1. Метод прямоугольников
Вычисление
интеграла
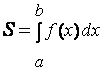
равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x=a, x=b и «боковыми сторонами» y=0, y=f(x) (рис. 1.1).
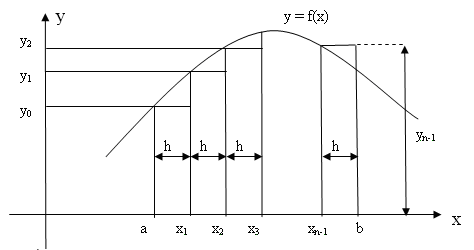
Рис. 1. 1.
Разобьем интервал интегрирования на n равных частей, каждая длиной h=(b-a)/n.
Приближенное значение
интеграла получается в виде сумм площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала, т.е. формула численного интегрирования имеет
вид (1.2):
|
|
или |
|
(1.2) |
и называется формулой «левых» прямоугольников.
Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала, то формула численного интегрирования будет иметь вид (1.3) и называется формулой «правых» прямоугольников:
|
|
(1.3) |