ГЛАВА 1
ОСНОВЫ АЛГОРИТМИЗАЦИИ
1.1. Этапы решения задач с
помощью компьютера
Понятие
“решение задачи” с помощью компьютера включает в себя гораздо больше, чем
просто вычисления на компьютере. Это процесс, в котором можно выделить
следующие этапы:
1. Постановка задачи и определение конечных целей.
2.
Математическое
описание задачи, т.е. формулировка конкретной инженерной, физической,
экономической задачи на языке математики.
3.
Выбор метода
решения задачи.
4.
Разработка
алгоритма решения задачи в соответствии с выбранным методом.
5.
Составление
программы на одном из языков программирования.
6.
Отладка
программы, т.е. поиск и исправление ошибок.
7.
Вычисления по
программе, которые проводятся обычно для нескольких вариантов набора исходных
данных.
8.
Интерпретация
результатов в терминах физического содержания задачи. При этом часто
оказывается, что нужно частично или полностью повторить предшествующие этапы,
пока задача действительно не будет решена.
1.2. Алгоритм: определение
и свойства
Алгоритм – это точно
определенное описание способа решения задачи в виде конечной последовательности
действий.
Свойства алгоритма:
1. Дискретность. Алгоритм выполняется по шагам и каждое
действие начинается после того, как завершено выполнение предыдущего действия.
2. Детерминированность (определенность). Результат применения алгоритма к
каждому конкретному набору исходных данных однозначен.
3. Результативность. Выполнение алгоритма должно завершиться получением
определенных результатов.
4. Конечность.
Алгоритм завершает работу за конечное число шагов.
5. Массовость.
Алгоритм должен быть применим для решения класса задач, отвечающих общей
постановке задачи.
1.3. Запись алгоритма в
виде блок-схем
Существует несколько способов описания алгоритмов: словесный, операторный, в виде блок-схем. В последнем
способе вычислительный процесс расчленяется на отдельные операции, изображаемые
в виде условных графических блочных символов. Внутри блоков указывается
поясняющая информация, характеризующая выполняемые ими действия. В таблице 1
приведены наиболее часто употребляемые блоки и даны пояснения к ним.
Таблица 1
|
Наименование символа |
Изображение символа |
Примечание |
|
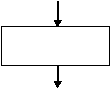
Процесс |
|
Вычислительное действие
или последовательность вычислительных действий. Арифметический
блок |
|
Принятие решения |
|
Проверка условий Логический блок |
|
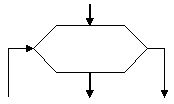
Модификация |
|
Начало и конец
цикла |
|
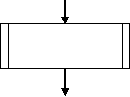
Предопределенный процесс |
|
Вычисления по
подпрограмме |
|
Передача данных |
|
Ввод данных или
вывод данных и печать результатов |
|
Прерывание |
|
Начало, конец,
пуск, останов |
|
Соединитель |
|
Разрыв линий
потока информации |
Описание алгоритмов с помощью блок-схем является
наиболее наглядным и не зависит от конкретного языка программирования.
1.4. Основные типы
вычислительных алгоритмов
Наиболее простым видом алгоритма является линейный
алгоритм, при котором действия выполняются последовательно, одно за другим, без
разветвлений и возвратов.
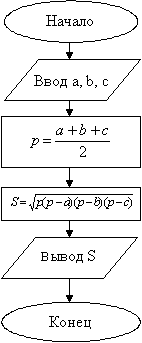
Пример.
Вычисление площади треугольника по трем сторонам a, b, c по формуле Герона:
![]() , где
, где
![]() .
.
Блок-схема алгоритма имеет вид:
В процессе решения многих задач часто возникает необходимость
в зависимости от исходных данных или получающихся промежуточных результатов
проводить вычисления либо по одним, либо по другим формулам, т.е. по разным
направлениям – ветвям. Такой вычислительный алгоритм называется разветвляющимся.
Пример.
Нахождение действительных корней квадратного уравнения
ax2 + bx + c = 0
Блок-схема алгоритма имеет вид:

При решении большинства практических задач возникает необходимость
неоднократного повторения однотипных действий при различных значениях
параметров, определяющих эти действия. Такие алгоритмы называются циклическими,
а повторяемые участки вычислений – циклами.
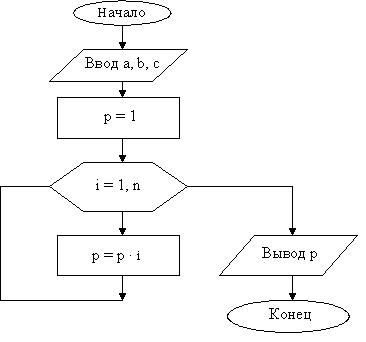
Пример.
Вычисление факториала натурального числа
n! = 1× 2× 3× ... × n
Блок-схема алгоритма имеет вид: