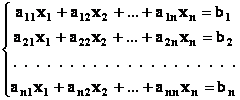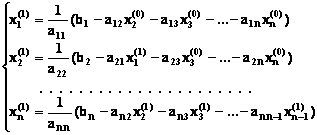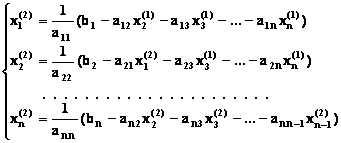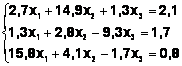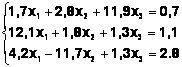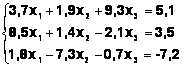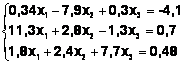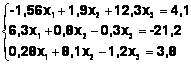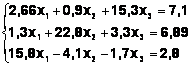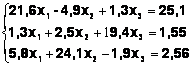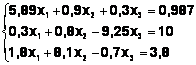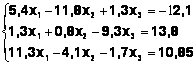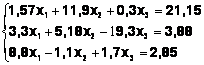2. Решение систем линейных алгебраических уравнений

Системы линейных алгебраических уравнений (СЛАУ) широко используются во многих областях прикладной математики. Оставляя за рамками данной работы вопросы теории линейных систем, отметим, что некоторые СЛАУ могут вообще не иметь решения или иметь бесконечное множество решений. В дальнейшем мы будем рассматривать только системы, имеющие единственное решение.

В общем виде система из n уравнений с n неизвестными выглядит так:

(2.1)

Таким образом, даны квадратная матрица коэффициентов при неизвестных {a_ij}, i, j = 1, 2, … , n, и вектор-столбец свободных членов (правых частей уравнений) {b_i}, i = 1, 2, … , n. В результате решения требуется определить n неизвестных x₁, x₂, … , x_n, которые удовлетворяют одновременно всем уравнениям системы.

Все методы решения СЛАУ делятся на две группы – прямые и итерационные. Прямые методы дают решение после выполнения конечного числа операций. Эти методы достаточно универсальны, но в ряде случаев полученное решение не является достаточно точным. Итерационные методы используют последовательные приближения (итерации) к искомому результату. Они позволяют получить решение с любой заданной точностью, но при их использовании заранее неизвестно количество предстоящих итераций, более того, итерационные методы в некоторых случаях вообще не дают решения.

В данном пособии мы рассмотрим по одному методу из каждой группы.

Метод Гаусса

Суть метода состоит в следующем. Вначале квадратную матрицу коэффициентов при неизвестных преобразуют в верхне-треугольную матрицу (прямой ход). Для этого сначала первое неизвестное исключают из второго и последующих уравнений системы, затем второе неизвестное исключают из третьего и последующих уравнений и так далее. Таким образом, в последнем уравнении остается только одно неизвестное. Для реализации прямого хода используют следующие известные правила:

- любое уравнение системы можно умножить на постоянный коэффициент;

- можно сложить два любых уравнения системы и результат записать вместо одного из этих уравнений.

На втором этапе последовательно вычисляют значения всех неизвестных, начиная с последнего (обратный ход).

Рассмотрим применение метода Гаусса на примере. Пусть имеем такую систему из трех уравнений:

(2.2)

Для исключения первого неизвестного из второго уравнения умножим первое уравнение на (-a₂₁/a₁₁), т.е. на –0,5. Первое уравнение примет вид

-2x₁ – 0,5x₂ + 0,5x₃ = -1,5.

Сложив его со вторым уравнением исходной системы (2.2), получим

– 2,5x₂ + 1,5x₃ = -0,5.

Можно заметить, что неизвестное x₁ в данном уравнении отсутствует.

Для исключения первого неизвестного из третьего уравнения системы (2.2) умножим первое уравнение этой системы на (-a₃₁/a₁₁), т.е. на –0,25. Первое уравнение примет вид

-x₁ – 0,25x₂ + 0,25x₃ = -0,75.

Сложив его с третьим уравнением исходной системы (2.2), получим

-1,25x₂ + 2,25x₃ = 4,25.

Можно заметить, что и в этом уравнении неизвестное x₁ отсутствует.

Таким образом, система (2.2) примет вид

4x₁ + x₂ – x₃ = 3

-2,5x₂ + 1,5x₃ = -0,5 (2.3)

-1,25x₂ + 2,25x₃ = 4,25

Теперь исключим неизвестное x₂ из третьего уравнения системы (2.3), сложив его со вторым уравнением системы (2.3), умноженным на –0,5. Получим систему

4x₁ + x₂ – x₃ = 3

-2,5x₂ + 1,5x₃ = -0,5 (2.4)

1,5x₃ = 4,5

Прямой ход закончен, исходная матрица коэффициентов приведена к верхне-треугольному виду. В третьем уравнении системы (2.4) присутствует только неизвестное x₃. Теперь легко осуществить обратный ход, т.е. вычислить неизвестные. Из третьего уравнения вычислим x₃, далее его значение подставим во второе уравнение и вычислим x₂, а затем из первого уравнения найдём x₁. Получим ответ: x₁ = 1; x₂ = 2; x₃ = 3. Задача решена.

Программа для решения СЛАУ методом Гаусса может иметь такой вид:

program SLAU1; {Решение системы линейных уравнений методом Гаусса}

uses crt;

const n=3;

var a:array [1..n,1..n] of real;

b,x: array [1..n] of real;

i,j,k: integer; c,s: real;

begin

{Ввод исходных данных}

for i:=1 to n do

begin

writeln (‘Введите коэффициенты уравнения’,i);

for j:=1 to n do read (a[i,j]);

writeln (‘Введите свободный член уравнения’,i);

readln (b[i]);

end;

{Прямой ход}

for k:=1 to n-1 do

begin

for i:=k+1 to n do

begin

c:=-a[i,k]/a[k,k]; a[i,k]:=0;

for j:= k+1 to n do a[i,j]:=a[i,j]+c*a[k,j];

b[i]:=b[i]+c*b[k];

end;

end;

{Oбратный ход}

x[n]:=b[n]/a[n,n];

for i:=n-1 downto 1 do

begin

s:=0;

for j:=i+1 to n do s:= s+a[i,j]*x[j];

x[i]:=(b[i]-s)/a[i,i];

end;

{Вывод результатов}

writeln (‘Решение системы’);

for i:=1 to n do write (x[i]:8:4);

writeln;

end.

Метод Гаусса-Зейделя

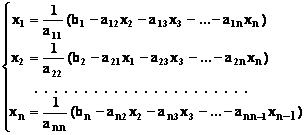
Данный метод является одним из самых распространенных итерационных методов решения СЛАУ, поскольку он отличается простотой и легкостью программирования. Рассмотрим его суть. Допустим, диагональные коэффициенты исходной матрицы {a_ij}отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему (2.1) в следующем виде:

(2.5)

Если теперь задать для неизвестных их начальные приближенные значения , то система (2.5) позволяет вычислить более точные значения неизвестных на первом шаге (на первой итерации):

(2.6)

Используя найденные значения неизвестных, можно еще более уточнить их на второй итерации:

(2.7)

и так далее.

В данном методе для нахождения значения i-го неизвестного на каждой итерации используются значения предыдущих неизвестных, уже найденные на данной итерации. Общую формулу определения i-го неизвестного на k-й итерации для системы n уравнений можно записать так:

i = 1, 2, … , n; k = 1, 2, …

(2.8)

Итерационный процесс продолжается до тех пор, пока все значения x_i^(k), не станут достаточно близкими к x_i^(k-1). Близость этих значений можно охарактеризовать максимальной абсолютной величиной их разности d. Тогда при заданной точности вычислений e > 0 критерий окончания итерационного процесса можно записать в виде:

(2.9)

При выполнении этого условия итерационный процесс называется сходящимся. В этом случае максимальные разности между значениями соответствующих неизвестных в двух последовательных итерациях убывают, а сами значения стремятся к решению системы.

Доказано, что для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения были не меньше суммы модулей всех остальных коэффициентов:

,

(2.10)

При этом хотя бы для одного уравнения неравенство (2.10) должно выполняться строго.

В качестве примера рассмотрим решение методом Гаусса-Зейделя системы (2.2). Заметим, что достаточное условие сходимости итерационного процесса (2.10) для этой системы соблюдается. Запишем исходную систему в виде:

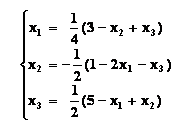
В качестве начальных приближений возьмем нули, т.е. примем x₂⁽⁰⁾ = x₃⁽⁰⁾= 0.

Найдем значения неизвестных на первой итерации:

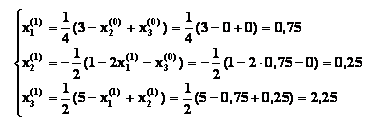
Далее произведем вторую итерацию:

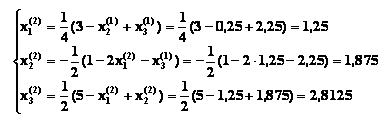
Производя аналогично третью и последующие итерации, найдем:

x₁⁽³⁾ = 0,984; x₂⁽³⁾ = 1,981; x₃⁽³⁾ = 2,953;

x₁⁽⁴⁾ = 1,015; x₂⁽⁴⁾ = 1,992; x₃⁽⁴⁾ = 2,988;

x₁⁽⁵⁾ = 0,999; x₂⁽⁴⁾ = 1,993; x₃⁽³⁾ = 2,997.

Нетрудно заметить, что разности между значениями соответствующих неизвестных в процессе итераций убывают, следовательно, процесс решения сходящийся, что и следовало ожидать. Если принять точность вычислений e = 0,02, то итерации следует закончить. При увеличении заданной точности вычисления корней, число итераций возрастает, например, при e = 0,00001 следует выполнить 11 итераций, а результат будет x₁⁽¹¹⁾ = 1,000000; x₂⁽¹¹⁾ = 1,999998; x₃⁽¹¹⁾ = 2,999999.

Программа для решения СЛАУ методом Гаусса-Зейделя приведена ниже. Поскольку при некорректной постановке задачи количество итераций может стать излишне большим, в программе предусмотрено прекращение итерационного процесса при превышении заранее заданного предельного числа итераций.

program SLAU2; {Решение системы методом Гаусса-Зейделя}

label 1,2,3;

const n=3;

var a:array [1..n,1..n] of real;

b,x:array [1..n] of real;

i,j,k,m:integer;

e,s,d,d1,c:real;

begin

{Ввод исходных данных}

for i:=1 to n do

begin

writeln (‘Введите коэффициенты уравнения’,i);

for j:=1 to n do read (a[i,j]);

writeln (‘Введите свободный член уравнения’,i);

readln (b[i]);

end;

writeln ('Введите точность');readln (e);

writeln ('Введите допустимое кол-во итераций');readln (m);

for i:=2 to n do x[i]:=0;

{Решение системы}

k:=1;

repeat

d1:=0;

for i:=1 to n do

begin

s:=0;

for j:=1 to n do

begin

if i=j then goto 1;

s:=s+a[i,j]*x[j];

1: end;

c:=(b[i]-s)/a[i,i];

d:=abs(c-x[i]);

if d1<d then d1:=d;

x[i]:=c;

end;

k:=k+1;

if k>m then goto 2;

until d1<e;

{Вывод результатов}

writeln (‘решение системы’);

for i:=1 to n do write (x[i]:8:4);

writeln; goto 3;

2: writeln ('Количество итераций выше допустимого');

3:end.

Задания. Решить систему линейных алгебраических уравнений:

Таблица 3

№ варианта	Система	Метод решения
0		Метод Гаусса
1		Метод Гаусса-Зейделя (ε = 0,0001)
2		Метод Гаусса
3		Метод Гаусса-Зейделя (ε = 0,0001)
4		Метод Гаусса
5		Метод Гаусса-Зейделя (ε = 0,0001)
6		Метод Гаусса
7		Метод Гаусса-Зейделя (ε = 0,0001)
8		Метод Гаусса
9		Метод Гаусса-Зейделя (ε = 0,0001)