Untitled

Модели

Исходным шагом для применения метода CPM является описание проекта в виде перечня выполняемых работ с указанием их взаимосвязи. Для описания проекта используются два основных способа: табличный и графический. Рассмотрим следующую таблицу, описывающую проект.

Работа	Непосредственно предшествующая работа	Время выполнения
A	-	t_A
B	-	t_B
C	B	t_C
D	A, C	t_D

В первом столбце указаны наименования всех работ проекта. Их четыре: A, B, C, D. Во втором столбце указаны работы, непосредственно предшествующие данной. У работ A и B нет предшествующих. Работе C непосредственно предшествует работа B. Это означает, что работа C может быть начата только после того, как завершится работа B. Работе D непосредственно предшествуют две работы: A и C. Это означает, что работа D может быть начата только после того, как завершатся работы A и C. В третьем столбце таблицы для каждой работы указано время ее выполнения. На основе этой таблицы может быть построено следующее графическое описание проекта.

На рисунке проект представлен в виде графа с вершинами 1, 2, 3, 4 и дугами A, B, C, D. Каждая вершина графа отображает событие. Событие 1 означает начало выполнения проекта. Иногда такое событие обозначают буквой S (start). Событие 4 означает завершение проекта. Для обозначения такого события иногда используется буква F (finish). Любая работа проекта – это упорядоченная пара двух событий. Например, работа A есть упорядоченная пара событий (1,3). Работа D - упорядоченная пара событий (3,4). Событие проекта состоит в том, что завершены все работы, "входящие" в соответствующую вершину. Например, событие 3 состоит в том, что завершены работы A и C.

Рассмотрим другой проект, представленный следующей таблицей.

Работа	Непосредственно предшествующая работа	Время выполнения
A	-	t_A
B	-	t_B
C	B	t_C
D	A, C	t_D
E	C	t_E
F	C	t_F
G	D, E, F	t_G

Графическое описание проекта, построенное по этой таблице, имеет следующий вид.

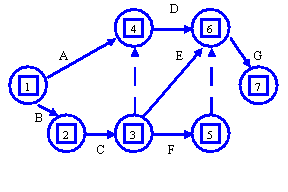
В этом графическом описании проекта кроме тех работ, которые указаны в таблице, использованы две "фиктивные" работы (3,4) и (5,6). На рисунке эти работы показаны пунктиром. Эти работы не требуют времени на их выполнение и используются в графическом представлении проекта лишь для того, чтобы правильно отобразить взаимосвязь между работами.

Получив графическое представление проекта, мы обеспечили себе возможность провести расчеты по методу CPM.

Определения.

Путь – последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. рис. выше), {A, D, G} и {C, F} – два различных пути.

Длина пути – суммарная продолжительность выполнения всех работ пути.

Критический путь – путь, суммарная продолжительность выполнения всех работ которого является наибольшей.

Ясно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.

Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод CPM позволяет получить критический путь намного проще.

Пусть i и j - вершины или события проекта, (i,j) - работа проекта, s - событие "начало проекта" (start)., f - событие "окончание проекта" (finish), T - длина критического пути.

Введем следующие обозначения:

t(i,j) - время выполнения работы (i,j),

ES(i,j) - наиболее раннее время начала работы (i,j),

EF(i,j) - наиболее раннее время окончания работы (i,j),

LS(i,j) - наиболее позднее время начала работы(i,j),

LF(i,j) наиболее позднее время окончания работы (i,j),

Ei - наиболее раннее время наступления события i,

Li - наиболее позднее время наступления события i.

R(i,j) - полный резерв времени на выполнение работы (i,j) (время, на которое может быть отложена работа (i,j) без увеличения продолжительности выполнения всего проекта).

r(i,j) - свободный резерв времени на выполнение работы (i,j), (время, на которое может быть отложена работа (i,j) без увеличения наиболее раннего времени Ej наступления последующего события j).

Если (i,j) - работа проекта, то имеют место соотношения:

для любого j : ES(i,j) = Ei ;

для любого i : LF(i,j) = Lj.

Для того, чтобы использовать метод CPM для нахождения критического пути, необходимо для каждой работы (i,j) определить величины:

наиболее раннее время начала работы ES(i,j),

наиболее раннее время окончания работы EF(i,j),

наиболее позднее время начала работы LS(i,j),

наиболее позднее время окончания работы LF(i,j).

Метод CPM описывается следующими соотношениями.

1. ES(s,j) = 0 для любой работы (s,j), выходящей из стартовой вершины s проекта.

2. EF(i,j) = ES(i,j) + t(i,j) = Ei + t(i,j) : наиболее раннее время окончания любой работы (i,j) превышает наиболее раннее время начала этой работы (время наступления предшествующего события i) на время ее выполнения.

3. ES(q,j) = maxi EF(i,q) = E q : наиболее раннее время начала работы (q,i) равно наибольшему из значений наиболее раннего времени окончания непосредственно предшествующих ей работ.

4. T = E f = maxi EF(i, f) : длина критического пути равна наиболее раннему времени завершения проекта.

5. LF(i, f) = T: наиболее позднее время окончания любой работы, завершающей проект, равно длине критического пути.

6. LS(i,j) = LF(i,j) - t(i,j) = Lj - t(i,j): наиболее позднее время начала любой работы меньше наиболее позднего времени окончания этой работы (времени наступления последующего события) на время ее выполнения.

7. LF(i,q) = minj LS(q,j)= Lq : наиболее позднее время окончания работы (i,q) равно наименьшему из значений наиболее позднего времени начала непосредственно следующих за ней работ.

8. R(i,j) = LS(i,j) - ES(i,j) = LF(i,j) - EF(i,j) = Lj - t(i,j) - Li: полный резерв времени выполнения любой работы равен разности между наиболее поздним и наиболее ранним временем ее начала или разности между наиболее поздним и наиболее ранним временем ее окончания.

9. r(i,j) = Lj - ES(i,j) - t(i,j) = Lj - EF(i,j) = Lj - Ei - t(i,j): свободный резерв времени выполнения любой работы равен разности между наиболее поздним временем наступления последующего события и наиболее ранним временем окончания работы.

Из приведенных выше определений и соотношений непосредственно следует:

1) Длина критического пути равна T.

2) Если R(i,j) = 0, то работа (i,j) лежит на критическом пути; если R(i,j) і 0, то работа (i,j) не лежит на критическом пути.

3) Если время начала работы (i,j), которая не лежит на критическом пути, отложить на срок меньший, чем r(i,j), то наиболее раннее время наступления последующего события не изменится.

4) Если время начала работы (i,j), которая не лежит на критическом пути, отложить на срок меньший, чем R(i,j), то время, необходимое на выполнение всего проекта, не увеличится.