В задачах поиска предполагается, что все данные хранятся в памяти с определенной идентификацией и, говоря о доступе, имеют в виду прежде всего доступ к данным (называемым ключами), однозначно идентифицирующим связанные с ними совокупности данных.

Пусть нам необходимо организовать доступ к файлу, содержащему набор одинаковых записей, каждая из которых имеет уникальное значение ключевого поля. Самый простой способ поиска - последовательно просматривать каждую запись в файле до тех пор, пока не будет найдена та, значение ключа которой удовлетворяет критерию поиска. Очевидно, этот способ весьма неэффективен, поскольку записи в файле не упорядочены по значению ключевого поля. Сортировка записей в файле также неприменима, поскольку требует еще больших затрат времени и должна выполняться после каждого добавления записи. Поэтому, поступают следующим образом - ключи вместе с указателями на соответствующие записи в файле копируют в другую структуру, которая позволяет быстро выполнять операции сортировки и поиска. При доступе к данным вначале в этой структуре находят соответствующее значение ключа, а затем по хранящемуся вместе с ним указателю получают запись из фала.

Существуют два класса методов, реализующих доступ к данным по ключу:

• методы поиска по дереву,
• методы хеширования.

1.2.1.Методы поиска по дереву.

Число порожденных отдельного узла (число поддеревьев данного корня) называется его степенью. Узел с нулевой степенью называют листом или концевым узлом. Максимальное значение степени всех узлов данного дерева называется степенью дерева.

Если в дереве между порожденными узлами, имеющими общий исходный, считается существенным их порядок, то дерево называется упорядоченным. В задачах поиска почти всегда рассматриваются упорядоченные деревья.

Упорядоченное дерево, степень которого не больше 2 называется бинарным деревом. Бинарное дерево особенно часто используется при поиске в оперативной памяти. Алгоритм поиска: вначале аргумент поиска сравнивается с ключом, находящимся в корне. Если аргумент совпадает с ключом, поиск закончен, если же не совпадает, то в случае, когда аргумент оказвается меньше ключа, поиск продолжается в левом поддереве, а в случае когда больше ключа - в правом поддереве. Увеличив уровень на 1 повторяют сравнение, считая текущий узел корнем.

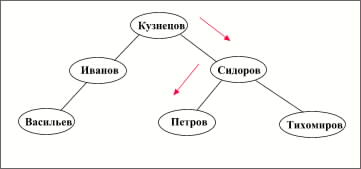
Пример: Пусть дан список студентов, содержащий их фамили и средний бал успеваемости (см. таблицу 1.1). В качестве ключа используется фамилия студента. Предположим, что все записи имеют фиксированную длину, тогда в качестве указателя можно использовать номер записи. Смещение записи в файле в этом случае будет вычислятся как ([номер_записи] -1 ) * [длина_записи]. Пусть аргумент поиска "Петров". На рисунке 1.2 показаны одно из возможных для этого набора данных бинарных деревьев поиска и путь поиска.

Заметим, что здесь используется следующее правило сравнения строковых переменных: считается, что значение символа соответствует его порядковому номеру в алфавите. Поэтому "И" меньше "К", а "К" меньше "С". Если текущие символы в сравниваемых строках совпадают, то сравниваются символы в следующих позициях.

Бинарные деревья особенно эффективны в случае когда множество ключей заранее неизвестно, либо когда это множество интенсивно изменяется. Очевидно, что при переменном множестве ключей лучше иметь сбалансированное дерево.

Определение: Бинарное дерево называют сбалансированным (balanced), если высота левого поддерева каждого узла отличается от высоты правого поддерева не более чем на 1.

При поиске данных во внешней памяти очень важной является проблема сокращения числа перемещений данных из внешней памяти в оперативную. Поэтому, в данном случае по сравнению с бинарными деревьями более выгодными окажутся сильно ветвящиеся деревья - т.к. их высота меньше, то при поиске потребуется меньше обращений к внешней памяти. Наибольшее применение в этом случае получили В-деревья (В - balanced)

Определение: В-деревом порядка n называется сильно ветвящееся дерево степени 2n+1, обладающее следующими свойствами:

1. Каждый узел, за исключением корня, содержит не менее n и не более 2n ключей.
2. Корень содержит не менее одного и не более 2n ключей.
3. Все листья расположены на одном уровне.
4. Каждый нелистовой узел содержит два списка: упорядоченный по возрастанию значений список ключей и соответсвующий ему список указателей (для листовых узлов список указателей отсутствует).

Для такого дерева:

• сравнительно просто может быть организован последовательный доступ, т.к. все листья расположены на одном уровне;
• при добавлении и изменении ключей все изменения ограничиваются, как правило, одним узлом.

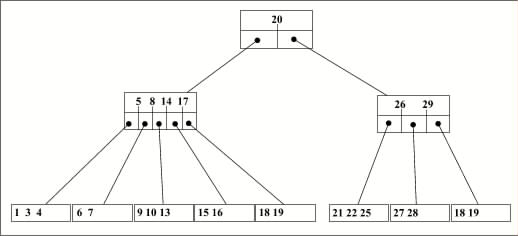
В-дерево, в котором истинные значения содержатся только в листьях (концевых узлах), называется В+-деревом. Во внутренних узлах такого дерева содержатся ключи-разделители, задающие диапазон изменения ключей для поддеревьев.

Подробнее о различных видах сбалансированных деревьев, а также методах их реализации можно прочитать в литературе, список которой приведен в конце страницы. Следует отметить, что B- деревья наилучшим образом подходят только для организации доступа к достаточно простым (одномерным) структурам данных. Для доступа к более сложным структурам, таким, например, как пространственные (многомерные) данные в последнее время все чаще используют R-деревья.

R-дерево (R-Tree) это индексная структура для доступа к пространственным данным, предложенная А.Гуттманом (Калифорнийский университет, Беркли). R-дерево допускает произвольное выполнение операций добавления, удаления и поиска данных без периодической переиндексации.

Для представления данных используются записи, каждая из которых имеет уникальный идентификатор (tuple-identifier). В каждом концевом узле (листе) дерева содержится запись вида (I,tuple-identifier), где I - n-мерный параллелепипед, содержащий указатели на пространственные данные (его также называют minimal bounding rectangle, MBR), а каждый элемент в tuple-identifier содержит верхнюю и нижнюю границу параллелепипеда в соответствующем измерении.

Неконцевые узлы содержат записи вида (I, childnode-pointer), где I минимальный ограничивающий параллелепипед для MBR всех узлов, производных по отношению к данному. Childnode-pointer - это указатель на производные узлы.

Пусть M и m <= M/2 соответственно максимальное и мимимальное количество элементов, которое может быть размещено в узле. Тогда свойства R-дерева можно описать следующим образом:

• R-Tree является сильно сбалансированным деревом, т.е. все листья находятся на одном уровне.
• Корневой узел имеет, как минимум, двух потомков.
• Для каждого элемента (I, childnode-pointer) в неконцевом узле I является наименьшим возможным параллелепипедом, т.е. содержит все параллелепипеды производных узлов.
• Каждый концевой узел (лист) содержит от m до M индексных записей.
• Для каждой индексной записи (I, tuple-identifier) в концевом узле I является параллелепипедом, который содержит n-мерный объект данных, на который указывает tuple-identifier

1.2.2.Хеширование.

Если множество ключей заранее неизвестно или очень велико, то от идеи однозначного вычисления адреса записи по ее ключу отказываются, а хеш-функцию рассматривают просто как функцию, рассеивающую множество ключей во множество адресов.

Литература: 

Н.Вирт. Алгоритмы и структуры данных.-М.:"Мир",1989.
М.Сибуя, Т.Ямамото. Алгоритмы обработки данных.-М.:"Мир",1986.

Следующая глава:2.1.Представление данных с помощью модели "сущность-связь".