4.2. Методы построения функций принадлежности
Вопрос о построении функций принадлежности (F-функций) является одним из самых важных вопросов в теории нечетких множеств [23, 66, 134], но эта проблема не является уникальной только для теории нечетких множеств [350].
В работе [173] предложена модель фундаментального измерения нечеткости. Нечеткость измерения интенсивности какого-либо свойства Р, которым обладает некоторый объект, может заключаться в сложности, неточном измерении этой интенсивности, или из-за того, что индивидуумы могут по-разному воспринимать интенсивность этого свойства Р [173]. Для представления функции принадлежности нечеткого множества используется техника теории измерения и шкалирования [191].
Аналогичные проблемы возникают при построении характеристических функций в теории полезности [118, 231].
При построении
функций принадлежности основным
является понятие относительного
предпочтения одного режима работы
системы перед другим, т.е. для двух
режимов работы х1 и х2 можно записать ![]() в том случае, когда
режим х2
более предпочтителен (с точки
зрения эффективности и
допустимости), чем х1. Предпочтительность
одного режима работы перед другим
может быть вызвана причинами
технологического, экономического,
надежностного, экологического
характера и различными
субъективными причинами,
вызванными неформальными
сведениями, которыми обладает лицо,
принимающее решение.
в том случае, когда
режим х2
более предпочтителен (с точки
зрения эффективности и
допустимости), чем х1. Предпочтительность
одного режима работы перед другим
может быть вызвана причинами
технологического, экономического,
надежностного, экологического
характера и различными
субъективными причинами,
вызванными неформальными
сведениями, которыми обладает лицо,
принимающее решение.
Функция
принадлежности ![]() и ставит в
соответствие каждому режиму
и ставит в
соответствие каждому режиму ![]() число из интервала [0,1],
характеризующее степень
принадлежности решения к
подмножеству D
эффективных и допустимых решений.
число из интервала [0,1],
характеризующее степень
принадлежности решения к
подмножеству D
эффективных и допустимых решений.
Естественным
является также и требование
непрерывности функции ![]() , которое формализует
интуитивное представление о том,
что если два решения множества Х
отличаются друг от друга лишь
незначительно, то значения функций
принадлежности для этих решений
также близки [98].
, которое формализует
интуитивное представление о том,
что если два решения множества Х
отличаются друг от друга лишь
незначительно, то значения функций
принадлежности для этих решений
также близки [98].
Функция ![]() должна быть
согласована с отношением
должна быть
согласована с отношением ![]() , т.е.
, т.е. ![]() , тогда и только тогда,
когда
, тогда и только тогда,
когда ![]() .
.
Конкретный вид функций принадлежности определяется на основе различных дополнительных предположений о свойствах этих функций (симметричность, монотонность, непрерывность первой производной и т.д.) с учетом специфики имеющейся неопределенности, реальной ситуации на объекте и числа степеней свободы в функциональной зависимости.
Соответствующие теоремы представления и единственности функций принадлежности при наличие полной системы аксиом могут быть доказаны на основе аксиоматических методов [274, 279, 173]. Показано, как можно построить числовое представление принадлежности на шкале интервалов и шкале отношений [172, 173]. Проведен сравнительный анализ прямого и обратного оценивания, групповых и индивидуальных функций принадлежности [172].
Во многих практических ситуациях функция принадлежности должна быть оценена исходя из частичной информации о ней, скажем такой, как значения, принимаемые ею на конечном множестве опорных точек х1,...,хn. В этом случае говорят, что она частично определена с помощью "поясняющего примера".
В работе [251] для оценки функций принадлежности используется понятие множества уровня. Этот метод позволяет определить степень принадлежности элементов к нечеткому подмножеству А с учетом известных вероятностей выборки элементов множества Х для фиксированных r-уровней.
В практических приложениях применяются методы определения характеристических функций (или построения их оценок) по выборкам и на основании априорной информации, в которую входят ограничения на эти функции [84, 254]. Если априорной информации о свойствах характеристических функций недостаточно для построения определенных функций, которые были бы "оптимальны" в каком-то смысле, приходится прибегать к эвристическим методам нахождения этих функций с последующей экспериментальной проверкой "качества" выбранных функций [84, 254].
На рис.2.2. приведены все основные виды функций принадлежности, применяемые в теории нечетких множеств [65, 98, 99, 110, 129, 281, 353].
|
|
|
|
|
|
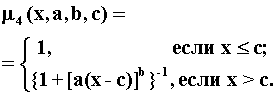 |
|
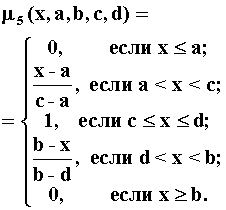 |
|
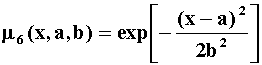 |
|
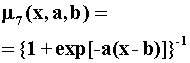 |
|
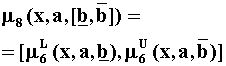 |
|
Рис.4.1. Примеры различных способов построения функций принадлежности.
Для решения
многокритериальных задач
используются различные методы
построения обобщенного показателя,
причем одним из наиболее удобных
способов является обобщенная
функция желательности Харрингтона
[3]. Функция желательности может
быть использована как функция
принадлежности, т.к. d![]() [0,1]. Она возникла в
результате наблюдений за реальными
решениями экспериментаторов и
обладает такими полезными
свойствами как непрерывность,
монотонность и гладкость. Кроме
того эта кривая хорошо передает тот
факт , что в областях
желательностей, близких к 0 и 1,
"чувствительность" ее
существенно ниже, чем в средней
зоне (рис.2.3.) [3]. В этом случае
функция принадлежности может быть
задана уравнением
[0,1]. Она возникла в
результате наблюдений за реальными
решениями экспериментаторов и
обладает такими полезными
свойствами как непрерывность,
монотонность и гладкость. Кроме
того эта кривая хорошо передает тот
факт , что в областях
желательностей, близких к 0 и 1,
"чувствительность" ее
существенно ниже, чем в средней
зоне (рис.2.3.) [3]. В этом случае
функция принадлежности может быть
задана уравнением ![]() .
.
Стандартные
отметки на шкале желательности
приведены в табл. 4.1. Значение ![]() обычно соответствует
границе допустимых значений.
обычно соответствует
границе допустимых значений.
Таблица 4.1.
Желательность |
Отметки на шкале желательности |
| Очень хорошо | 1.00 - 0.80 |
| Хорошо | 0.80 - 0.63 |
| Удовлетворительно | 0.63 - 0.37 |
| Плохо | 0.37 - 0.20 |
| Очень плохо | 0.20 - 0.00 |
В работе [66] рассмотрены и исследованы различные способы получения функций принадлежности. Введена единая математическая форма представления различных способов определения функций принадлежности. Для описания нечетких множеств предложено применять сплайн-представление, в результате чего оказалось возможным выявить вклад того или иного источника информации в конечное решение.
Возможности построения многомерных функций принадлежности и аппроксимация их с помощью алгоритмов метода группового учета аргументов (МГУА) рассмотрены в работе [22]. В качестве примера для одного из УКПГ газового месторождения Медвежье построена функция принадлежности, зависящая от величины расхода и давления газа на УКПГ.
При использовании в качестве дополнительной переменной параметра времени t имеется возможность прогнозировать изменение функций принадлежности во времени и на их основе планировать ввод новых производственных мощностей и проведение различных ремонтных работ [134].
Разработаны также специальные преобразователи "аналог - функция принадлежности" [338], позволяющие получать функцию принадлежности непосредственно от датчика. Эти преобразователи удобно использовать в схемах коммутации, когда один сигнал вызывает несколько выходных в определенной последовательности, в логических схемах для обработки сильно зашумленных сигналов.
Предлагается также принцип аппаратурной реализации нескольких основных видов функций принадлежности, представляющих собой характеристику "вход - выход" элемента системы. Комбинированием элементов со специально подобранными функциями принадлежности можно стоить схемы со сложными нелинейными функциями [248].
В работе [314] для построения функций принадлежности на основе объективной информации и данных замеров предлагаются специальные блоки для выделения свойств ("property extractor"), например, с использованием детерминированного замера х* [314]
 . (4.1)
. (4.1)
В качестве ![]() берется
установившееся (или среднее)
значение параметра х, а величины
берется
установившееся (или среднее)
значение параметра х, а величины ![]() и
и ![]() выбираются с учетом особенностей
функции принадлежности и наилучших
результатов по распознаванию
сигналов (или управлению) в серии
экспериментов [314].
выбираются с учетом особенностей
функции принадлежности и наилучших
результатов по распознаванию
сигналов (или управлению) в серии
экспериментов [314].
Преимущества применения устройств, непосредственно построенных на элементах с многозначной логикой обсуждаются в работах [282, 284]. Отмечается перспективность использования многозначной логики для реализации регуляторов, устройств и систем с нечеткой логикой, которая может быть весьма полезной при создании систем принятия решений в условиях не полностью определенных данных.
В работе [336] предлагается реализация механизма нечеткого вывода на СБИС для возможности принятия решений при наличии неопределенных и приблизительных рассуждений. Проект устройства вывода основан на нечеткой арифметике и ориентирован на поддержку неопределенных знаний и способствует извлечению знаний человека-эксперта и имитации его процесса рассуждений. Быстродействие устройства около 80 тыс. ФЛИПС (нечетких логических выводов в секунду).
В Японии создан специальный Международный институт инженерных исследований по нечеткой логике (Laboratory for international Fuzzy Engineering Research). Основной задачей этого института является создание компьютера для приложений области нечеткой логики. Оцениваемый в 37 млн. долл. шестилетний бюджет института финансируется примерно 40 компаниями, среди которых Hitachi, Toshiba, Toyota.
В США налажено производство микропроцессора FC110, предназначенного для программирования задач нечеткой логики во встроенных прикладных коммерческих системах реального времени. Производит эти микропроцессоры фирма TogaiInfraLogic Inc. Концептуальная методология нечеткой логики, предусматривающая количественное представление неточных значений в программируемых алгоритмах, оказалась весьма полезной при решении задач искусственного интеллекта в реальном времени.
В задачах математического программирования параметры задач зависят от многих факторов, которые сложно учесть в модели [179]. Внесение этих зависимостей в модель значительно ее усложняет и повышает размерность задачи, а "уточнение модели таким путем на практике сведется на нет из-за невозможности измерить или измерить с достаточной точностью величины введенных в модель факторов" [179]. То есть, для параметров моделей более естественным было бы задание интервала возможных значений или функции принадлежности.
Вопросы приближения функций принадлежности и нечетких отношений и выбора среди функций принадлежности, согласованных с заданным отношением, такой, которая наилучшим образом приближает предъявленную, рассмотрены в [106].
Большая часть работ по проблеме построения F-функций связана с методами обработки экспертных данных и результатов опроса специалистов [65, 98, 99, 318]. Метод позволяет включить в состав ограничений на систему некоторые субъективные ограничения, которые могут быть вызваны тем, что человек обладает рядом неформальных сведений о системе на естественном языке.
Например, цель G вида "дебит скважины должен быть близок к 1,2 млн.м куб./сут" или ограничение С "дебит должен быть больше 0,8 млн.м куб./сут" могут быть представлены соответственно следующим образом:
![]() ; (4.2)
; (4.2)
 ; (4.3)
; (4.3)
В общем случае эти
лингвистические ограничения могут
быть представлены в виде ![]() (рис.4.1).
(рис.4.1).
Таким образом,
характер функции зависит от трех
параметров [289]: с - определяет точку
максимума функции принадлежности ![]() для b>0 или минимума
для b>0 или минимума ![]() для b< 0; а - размах кривой; b
- поведение фронтов
кривой.
для b< 0; а - размах кривой; b
- поведение фронтов
кривой.
В теории нечетких множеств отсутствуют различия между целями и ограничениями, заданными на множестве альтернатив Х, так как и цели, и ограничения представляются в виде функций принадлежности.
Для приведенного выше примера (4.2) - (4.3) нечеткое решение D с учетом цели G и ограничения С может быть представлено функцией принадлежности (рис.4.2)
![]() (4.4)
(4.4)
В качестве четкого решения по дебиту скважины может быть принято решение q*=1,36 млн.м3/сут., при котором функция принадлежности для нечеткого решения достигает максимального значения (рис.2.5).
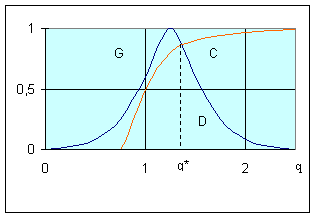
Рис.4.2.Нечеткое решение по выбору дебита скважины с учетом нечетких цели G и ограничения С.
С помощью функции принадлежности можно адекватно отразить мнение одного или нескольких экспертов. Это связано с неспособностью человека формулировать свое количественное впечатление в виде одиночного числа [179].
Пусть эксперт в
качестве оптимального дебита
скважины называет дебит 1,5 млн.м
куб./сут. Но это не
значит, что величины незначительно
отличающиеся от него будут
совершенно неприемлемыми, т.е.
степени принадлежности ![]() и
и ![]() будут
незначительно отличаться от
будут
незначительно отличаться от ![]() . Результат
экспертного опроса может
задаваться в виде таблицы или
непрерывной функции.
. Результат
экспертного опроса может
задаваться в виде таблицы или
непрерывной функции.
Пусть имеется m экспертов, часть
которых на вопрос о принадлежности
элемента x![]() X
нечеткому множеству A отвечает
положительно. Обозначим их число
через n1. Другая часть
экспертов n2=m-n1 отвечает на этот
вопрос отрицательно. Тогда
принимается, что
X
нечеткому множеству A отвечает
положительно. Обозначим их число
через n1. Другая часть
экспертов n2=m-n1 отвечает на этот
вопрос отрицательно. Тогда
принимается, что
![]()
Пример 4.1. Пусть имеется множество X={1, 2, 3, 4, 5} и требуется построить нечеткое множество A, формализующее нечеткое понятие “намного больше двух”. Допустим, что результаты опроса шести экспертов показаны в табл.4.2:
Таблица 4.2.
m |
1 |
2 |
3 |
4 |
5 |
n1 |
0 |
0 |
1 |
4 |
6 |
n2 |
6 |
6 |
5 |
2 |
0 |
Тогда получим следующие значения функции принадлежности элементов множества X нечеткому множеству A
A = <0/1, 0/2, 0.2/3, 0.7/4, 1/5 >
Однако чаще всего
при оценке параметров бывают
известны лишь интервальные
ограничения и наиболее допустимое
значение. Например, технолог может
не затрудняясь указать минимально
и максимально допустимые режимы [a,
b] и номинальную
производительность системы c. Если он не
располагает большей информацией,
то единственной приемлемой
аппроксимацией является линейная.
В этом случае рассматриваемый
параметр можно характеризовать
треугольной функцией
принадлежности ![]() (рис.4.1).
(рис.4.1).
Аппарат теории нечетких множеств и особенности операций позволяют отбраковывать некритические ограничения для конкретного режима работы системы. Это особенно важно, т.к. при решении практически важных задач число ограничений может быть очень большим. Практически в этом случае реализуется понятие о "наихудшем нарушенном ограничении" для исключения неактивных ограничений [237].
Если имеется обычная функция эффективности (например, функция затрат энергии, средств и т.д.), устанавливающая линейную упорядоченность на множестве альтернатив, то она может быть преобразована в функцию принадлежности с помощью нормализации, сохраняющей установленную линейную упорядоченность [173, 231].
В этом случае
операция принятия решений для
нечетких множеств по существу
сводится к синтезу глобального
критерия ![]() как
функции k
исходных критериев
как
функции k
исходных критериев ![]() , отражающих
эффективность и допустимость
режимов работы системы с
экономической, технологической,
надежностной и других точек зрения.
Причем максимум этого критерия
будет соответствовать четкому
решению многокритериальной задачи.
Тогда решение задачи будет
сводиться к обычной оптимизации
, отражающих
эффективность и допустимость
режимов работы системы с
экономической, технологической,
надежностной и других точек зрения.
Причем максимум этого критерия
будет соответствовать четкому
решению многокритериальной задачи.
Тогда решение задачи будет
сводиться к обычной оптимизации
![]() . (4.5)
. (4.5)
Согласно [194], эта функция должна быть инвариантна по отношению к преобразованию сдвига и к изменению масштаба любого критерия. Это требование может быть удовлетворено за счет правильного выбора частных критериев эффективности, которые должны быть инвариантны по отношению к преобразованию
![]() , (4.6)
, (4.6)
где ![]() - любое постоянное
число;
- любое постоянное
число; ![]() - любое
положительное число, т.е. должно
выполняться условие
- любое
положительное число, т.е. должно
выполняться условие
![]() . (4.7)
. (4.7)
Все эти требования можно удовлетворить, используя функцию вида
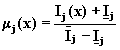 . (4.8)
. (4.8)
где ![]() - максимальное
значение критерия j;
- максимальное
значение критерия j; ![]() - минимальное значение
j-го критерия,
причем оно может выбираться с
позиций предельного режима
- минимальное значение
j-го критерия,
причем оно может выбираться с
позиций предельного режима ![]() , при котором работа
системы недопустима или совсем неэффективна с позиций
данного критерия - в этом случае
отпадает необходимость в
ранжировании частных критериев
, при котором работа
системы недопустима или совсем неэффективна с позиций
данного критерия - в этом случае
отпадает необходимость в
ранжировании частных критериев ![]() .
.
Используя, например, критерий максимизации давления на входе в магистральный трубопровод, можно построить следующую функцию для эффективных режимов ее работы
![]() .
.
На основе расчета предельно допустимого дебита qп для конуса пластовой воды строится функция
![]() ,
,
характеризующая риск обводнения скважины пластовыми водами. Тогда функция принадлежности для допустимых дебитов имеет следующий вид:
![]() .
.
Построенный
согласно этим требованиям критерий
![]() является показателем
степени принадлежности
определенного режима работы системы к
подмножеству допустимых или
эффективных режимов и изменяется
на интервале [0,1], что соответствует
определению функции
принадлежности Заде. Поэтому к
сформированным таким образом
критериям применимы минимаксные
операции Заде, и решение
многокритериальной задачи может
быть записано в виде
является показателем
степени принадлежности
определенного режима работы системы к
подмножеству допустимых или
эффективных режимов и изменяется
на интервале [0,1], что соответствует
определению функции
принадлежности Заде. Поэтому к
сформированным таким образом
критериям применимы минимаксные
операции Заде, и решение
многокритериальной задачи может
быть записано в виде
![]() . (4.9)
. (4.9)
Решение ![]() в этом случае будет
инвариантным по отношению к преобразованию (4.6)
критериев
в этом случае будет
инвариантным по отношению к преобразованию (4.6)
критериев ![]() .
.
Для решения задач определения максимума многомодальных систем обычное понятие максимальной величины функции f(х) не является достаточно информативным. "Более полезным является понятие максимизирующего множества, так как оно дает информацию не только о точке или точках, в которых функция принимает максимальное значение, но также и о степени приближения функции к максимальному значению в других точках на всем интервале ее изменения" [84].
В качестве примера в [84] приводится следующая функция принадлежности для максимизирующего множества М(f)
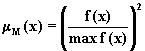 .
(4.10)
.
(4.10)
Вероятностный метод построения функций принадлежности основан на сходстве понятий нечеткости и вероятности [110]. Оба эти понятия используются при наличии неопределенности в системах, которая является следствием случайных факторов, неточности нашего знания или принципиальной невозможности и ненужности получения точных решений. Но даже в тех случаях , когда нечеткость в процессе принятия решений может быть представлена вероятностной моделью, обычно удобнее оперировать с ней методами теории нечетких множеств без привлечения аппарата теории вероятностей [110].
Многие авторы подчеркивают субъективность функции принадлежности в отличие от объективности вероятности как характеристики. Однако очень естественно определить функцию принадлежности таким образом, чтобы маловероятное с позиций теории вероятностей событие имело и малую степень принадлежности. "Нестатистическая" природа построения некоторых функций принадлежности для качественных параметров не означает, что в качестве таких функций нельзя использовать функции распределения вероятностей, нормированные определенным образом, т.е. в зависимости от типа нечетких переменных можно выделить два способа их построения - статистический и нестатистический [110]. Нечеткость и случайность могут употребляться в процессе принятия решений самыми разнообразными способами и в виде различных комбинаций.
Если для контролируемого параметра известна вероятность перехода системы от допустимого состояния к недопустимому в зависимости от назначенного для системы режима работы, то функция принадлежности, характеризующая степень риска принимаемого решения, может быть определена из условия предпочтения тех режимов, для которых степень риска меньше. Условие предпочтения может быть записано в следующей форме
![]() . (4.11)
. (4.11)
Тогда в качестве функции принадлежности мы можем принять функцию
![]() . (4.12)
. (4.12)
Эта функция
полностью удовлетворяет основным
требованиям к функции
принадлежности и монотонно
изменяется при варьировании режима
работы. Практически ![]() определяется на
основе построения гистограмм
накопленных частот перехода
подсистем в недопустимые состояния
для разных режимов работы.
Существует также подход
представления стохастических
величин как нечетких с
использованием теории возможности
Заде [318].
определяется на
основе построения гистограмм
накопленных частот перехода
подсистем в недопустимые состояния
для разных режимов работы.
Существует также подход
представления стохастических
величин как нечетких с
использованием теории возможности
Заде [318].
Например, пусть задана гистограмма накопленных частот срабатывания клапанов - отсекателей для газовых скважин (рис.4.3) (функция не доходит до значений, равных 1, так как некоторые клапаны вообще не срабатывают). Тогда функция принадлежности к подмножеству допустимых режимов для клапанов - отсекателей может быть записана в виде таблицы или в аналитической форме согласно (4.12).
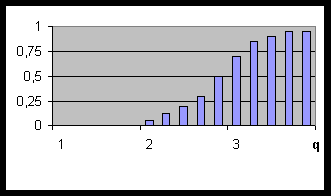
Рис. 4.3. Гистограмма накопленных частот для клапанов-отсекателей.
В работе [253] было проведено сравнение аппарата теории нечетких множеств и теории вероятностей в случае, когда стохастические переменные определяются на тех же базовых множествах что и соответствующие нечеткие переменные. делается заключение, что понятие неопределенности лучше выражается нечеткостью чем случайностью, а аппарат теории нечетких множеств вычислительно намного проще, чем теории вероятностей.
Вопросам использования аппарата теории вероятностей для проблем теории нечетких множеств посвящены работы [178, 273]. Однако сложности построения на практике необходимых для этого распределений априорных и условных вероятностей [83], серьезные недостатки различных подходов к определению теории вероятности [272] заставляет исследователей обращаться к невероятностным альтернативам. Важным преимуществом теории нечетких множеств является ее робастность, устойчивость к неточным оценкам [58, 170].
Альтернативой методу представления функции принадлежности путем записи для нее некоторого явного управления, является определение функции принадлежности как совокупности r-уровневых множеств [98, 166] или путем разбиения области значений функции на ряд непересекающихся сегментов [343]. Подход сегментного разбиения позволяет охарактеризовать нечеткое множество с помощью ряда функций принадлежности каждого из таких сегментов. В работе [343]предлагается метод нечеткой дискретизации таких сегментов с целью определения достаточного числа сегментов, необходимых для проведения расчетов с высокой точностью.
Имеется ряд работ, где авторами предлагаются методы построения и интерпретации F-функций на основе объективной технологической информации [22, 166, 260, 289].
В работе [195] отмечается, что потенциальные функции и меры сходства отличаются от функций принадлежности спецификой приложений, характером преодолеваемой неопределенности, допустимыми для них преобразованиями и операциями над ними.
Функции принадлежности для вышестоящих подсистем могут также строиться с использованием метода принятия решений в иерархических системах на основе функций принадлежности нижестоящих подсистем [134].
При управлении сложными системами в условиях неопределенности может использоваться понятие нечеткой обратной связи [121, 134]. Вопросы выбора оптимальных дебитов газовых скважин на основе этого метода обсуждаются в [121, 134]. Такой закон управления подсистемами "пласт - скважина" соответствует решению двухкритериальной задачи равномерной разработки залежи (например, равномерному падению пластового давления при равномерном стягивании контура газоводянного контакта).
Задача построения
одномерных и многомерных функций
принадлежности ![]() по наблюдениям за
объектом может быть решена
аналогично задаче оценивания линий
уровня r
многомерных плотностей
вероятностей
по наблюдениям за
объектом может быть решена
аналогично задаче оценивания линий
уровня r
многомерных плотностей
вероятностей ![]() [321].
[321].
При наличии неопределенности в процессе параметрической идентификации функций принадлежности может быть использовано понятие интервально-значных нечетких множеств [281].
Интервально-значное нечеткое множество (i-v нечеткое множество) А, определенное на множестве Х задается в виде
![]() ,
,
![]()
![]() . (4.13)
. (4.13)
Интервально-значную функцию принадлежности можно записать в виде
![]() .
(4.14)
.
(4.14)
Пример
интервально-значной функции
принадлежности ![]() приведен на рис.4.1, при
интервальном задании параметра
b.
приведен на рис.4.1, при
интервальном задании параметра
b.
Различные
операции с i-v
нечеткими множествами могут
выполняться аналогично
соответствующим операциям
нечетких множеств для нижних ![]() и верхних
и верхних ![]() граничных функций
принадлежности [281].
граничных функций
принадлежности [281].
Значительный прогресс в области построения функций принадлежности был достигнут в результате введения процедуры коррекции исходных функций принадлежности после принятия системного решения [39].
В условиях
значительной неопределенности
исходной информации возникают
ситуации, когда необходимо
принимать решения при отсутствии
точных сведений о структуре
объекта (например,
газотранспортной сети). В этом
случае удобно воспользоваться
понятием нечеткого графа [98],
описывающего структуру объекта.
Согласно терминологии нечетких
множеств матрица инцидентности
системы будет состоять уже не из
нулей и единиц, а из величин ![]() , характеризующих
возможность присутствия этой связи
S между
элементами i и j в системе.
, характеризующих
возможность присутствия этой связи
S между
элементами i и j в системе.
Нечеткой может быть и сама модель системы при отсутствии или высокой сложности отношения между входными и выходными переменными процесса. В этом случае нечеткая система описывается нечетким отношением R, а модель системы задается в виде [166]:
![]() ,
(4.15)
,
(4.15)
где ![]() есть элементы
нечеткого пространства состояний F(Х);
есть элементы
нечеткого пространства состояний F(Х); ![]() и
и ![]() .
.
Равенство (4.15) для функции принадлежности может быть записано в виде [98]
![]() .
(4.16)
.
(4.16)
Вопросам построения нечеткого отношения R по данным наблюдений посвящена работа [91].
Особенности теории нечетких множеств позволяют формализовать и включить в состав модели различные допущения, принимаемые при разработке алгоритма решения задачи. Такие понятия как "длинный" и "горизонтальный" газопровод, "стационарный" режим могут быть введены как лингвистические переменные по результатам степени влияния соответствующих допущений, исключенных членов уравнения на погрешность результата расчета. Эти функции очень легко построить по результатам исследований работ [102, 137, 291, 293].
Если в качестве меры нестационарности режима работы участка газопровода [144] выбрать величину
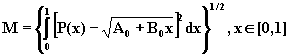 ,
(4.17)
,
(4.17)
где ![]() - параметры
стационарного распределения
давления: квадрат давления в начале
участка и
- параметры
стационарного распределения
давления: квадрат давления в начале
участка и ![]() соответственно, то функция
принадлежности режима к
подмножеству нестационарных
режимов может быть записана
следующим образом
соответственно, то функция
принадлежности режима к
подмножеству нестационарных
режимов может быть записана
следующим образом
![]() . (4.18)
. (4.18)
Величины а, b определяются на основе данных по погрешности измерения значений давления и допустимой погрешности у для модели стационарного режима. Например, для существующих датчиков замера давления в АСУ ТП КС и точности моделей нестационарного режима 3,5% b = 2; а = 2,3.
Для введения понятия "газопровод большого диаметра" можно воспользоваться результатами исследований [291, 293] влияния инерционного члена в уравнении нестационарного движения газа на погрешность расчета (с учетом того, что эта погрешность зависит от диаметра газопровода) (рис.4.4).
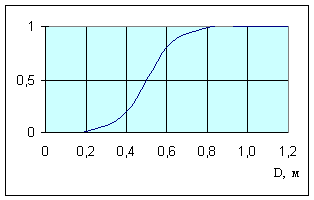
Рис. 4.4. Нечеткое понятие "газопровод большого диаметра"
Аналогично можно ввести понятие "длинный газопровод" для различных диаметров трубы (рис.4.5).
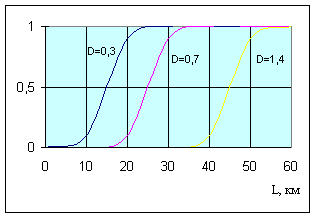
Рис.4.5. Нечеткое понятие "длинный газопровод"
Впервые связь между теорией нечетких множеств и теории катастроф была отмечена в работе [273]. Эта идея развита далее в работе [354], где рассмотрены некоторые особенности теории катастроф и показана возможность распространения на теорию катастроф некоторых идей нечетких множеств. Определенные функции, подробно рассмотренные в теории катастроф, поддаются в некоторых случаях интерпретации как функции принадлежности [354]. Использование таких функций может быть интересным для характеризации лингвистических описаний, которые изменяются во времени и отличаются одновременно дискретностью и нечеткостью [354].
В качестве простейшего примера может быть приведена катастрофа типа складки, которая может быть использована для моделирования работы компрессорной станции (КС) в условиях переключения с одной схемы включения газоперекачивающих агрегатов (ГПА) на другую.
Построение формализованных моделей или вывод физических законов проводится путем последовательного выдвижения предположений (гипотез) о характере процессов окружающей среды и системы контроля и управления для сведения исходной задачи на естественном языке к одной из типовых схем моделирования. Примерами таких гипотез могут служить предположения об однородности пласта, изотермичности процесса, его стационарности и т.д., причем степень правильности гипотезы для конкретного объекта может изменяться во времени.
Выполнение всех этих гипотез обычно проверяется исследователем для каждого конкретного случая применения этой модели. Вполне естественно, что точное выполнение гипотез на практике отсутствует, а соответствующих количественных характеристик степени применимости модели для каждой конкретной ситуации в настоящее время нет, и в модель процесса они не включаются. Между тем такие характеристики (например, степень неоднородности пласта, степень нестационарности процесса и т.д.) крайне важны, особенно при наличии нескольких моделей или иерархической системы моделей и необходимости их согласования и координации. Практически всегда существуют объективные методы оценки таких характеристик.
Ввиду отсутствия реальных жестких границ применимости моделей и существования целого ряда моделей, описывающих один и тот же технологический процесс с точки зрения различных наук и при различных исходных допущениях, вполне естественным является применение аппарата теории нечетких множеств для согласования и координации моделей. Одним из способов представления и учета степени применимости модели может служить несколько обобщенный способ согласования прогнозирующих моделей [260].
Пусть решение по
каждой из m
моделей задано нечетким множеством
![]() на оси решений Х, тогда
согласованное решение D может быть представлено как
пересечение частных нечетких
решений
на оси решений Х, тогда
согласованное решение D может быть представлено как
пересечение частных нечетких
решений
![]() .
.
Для каждого
нечеткого решения ![]() , будет задаваться
функция принадлежности
, будет задаваться
функция принадлежности
![]() , полученная в
результате исследования применимости модели
для процесса.
, полученная в
результате исследования применимости модели
для процесса.
Сам факт
выполнения k
предположений о характере
процессов учитывается введением
показателя ![]() , где
, где ![]() , причем в случае, когда
предположение j
о процессе для модели i идеально выполняется
, причем в случае, когда
предположение j
о процессе для модели i идеально выполняется ![]() , когда это
предположение не выполняется
, когда это
предположение не выполняется ![]() , и
, и ![]() в
остальных случаях. Тогда результирующая
функция принадлежности будет
выглядеть так:
в
остальных случаях. Тогда результирующая
функция принадлежности будет
выглядеть так:
![]() .
.
Параметры ![]() , характеризующие
нечеткость моделей при нарушении
условий их
существования, могут быть
определены объективно с учетом
дисперсии моделей, которая
получается в результате
идентификации моделей для реальных
объектов. В случае невозможности
объективной оценки показателя
, характеризующие
нечеткость моделей при нарушении
условий их
существования, могут быть
определены объективно с учетом
дисперсии моделей, которая
получается в результате
идентификации моделей для реальных
объектов. В случае невозможности
объективной оценки показателя ![]() он может быть определен на основе
экспертных оценок и должен
характеризовать относительно
других моделей степень
выполнимости предположений,
точность и применимость модели в
данной конкретной ситуации.
он может быть определен на основе
экспертных оценок и должен
характеризовать относительно
других моделей степень
выполнимости предположений,
точность и применимость модели в
данной конкретной ситуации.
Предлагаемый метод координации позволяет включить нечеткие условия существования моделей в состав системной модели и учесть их при согласовании частных решений. Описываемое явление может быть смоделировано путем введения понятия нечеткого отношения, которое также позволяет адекватно отразить неточность формул, нарушение законов за счет несоблюдения в каких-то конкретных условиях исходных допущений. Этот метод особенно удобен, когда трудно в количественной форме отразить условия существования модели.
В целом алгоритмы на базе нечетких множеств хорошо зарекомендовали себя на практике для самого разнообразного круга задач:
- для создания математической модели многослойного оценивания запасов угля в пластах [352];
- применение нечетких уравнений и элементов нечеткой логики для диагностирования сложных систем - пакет программ Thermix-2D для анализа динамики АЭС [290];
- при управлении нестационарным процессом движения морских геолого-геофизических комплексов [143];
- для оценки показателей качества программных средств [111];
- в системах искусственного интеллекта для управления работой технологического оборудования (фирмы "Тексако кемиклз" и "Экссон кемиклз") [117];
- в задачах контроля и управления системами разработки месторождений, добычи и транспорта газа [19, 22, 23, 26, 28, 31, 37, 38, 39, 127, 134, 136, 199];
- поведение диспетчерского персонала лучше всего описывается лингвистическими правилами поведения, а отклонение от принятых алгоритмов (ошибки и плохая работа диспетчеров, неисправности, возникшие помехи [164]) хорошо моделируется с использованием нечетких алгоритмов.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]