1. ОПИСАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН

Напомним методику описания случайных величин. Вероятность случайного события - это мера того, насколько велика возможность его возникновения. Вероятность изменяется от 0 до 1. Вероятность достоверного (которое точно произойдет) события равна 1. Напротив, вероятность невозможного события равна 0. Случайные величины являются более обобщенным понятием случайного события. Случайные величины могут быть дискретными или непрерывными. Дискретная случайная величина может принимать только определенные значения с определенной вероятностью. Например, на рис.2 показаны вероятности значений случайной величины Х.

Для описания как дискретных, так и непрерывных случайных величин используется функция распределения вероятности. Пусть Х - случайная величина и х - ее любое значение. Функция распределения вероятности определяется следующим образом:

т.е. она равна вероятности того, что случайная величина Х примет значение . Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие - значений, принимаемых случайными величинами. Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам:

1. , при ,
2. ,
3. - неубывающая функция х,
4. 

На рис.2 показаны примеры функций распределения вероятности.

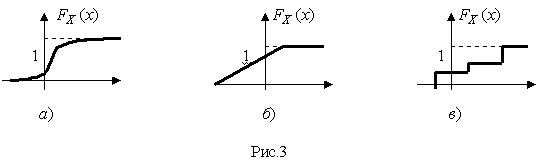
Функция распределения вероятности не всегда удобна для расчетов. Часто удобнее использовать не саму функцию , а ее производную. Она называется плотностью распределения вероятности

.

Физический смысл f(x) состоит в том, что произведение f(x)dx представляет вероятность попадания случайной величины Х в интервал от х до х + dx , т.е.

Свойства плотности распределения вероятности имеют вид:

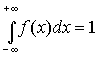- вероятность достоверного события равна 1 (свойство 1),
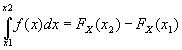- вероятность попадания случайной величины в интервал от до (свойство 2).

Пример. Случайная величина X имеет плотность распределения вероятности следующего вида:

f(х) = с, при -5 <x<-2,
f(х) = , при других х , где - дельта-функция.

Это проиллюстрировано на рис. 4. Необходимо вычислить параметр с.

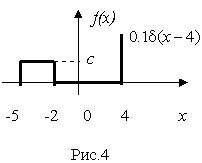
Этот пример относится к непрерывной случайной величине, которая может принимать и дискретное значение. Учитывая 1-е свойство плотности распределения вероятности и интегрирующее свойство дельта-функции, получим

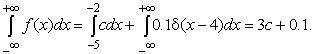
Из данных вычислений следует, что с = 0.3. Рассмотрим вопрос - как можно смоделировать случайную величину? В настоящее время в связи с большой популярностью вычислительной техники широко используется так называемый алгоритмический способ.