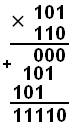2.9. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ

УМНОЖЕНИЕ

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Умножение в двоичной системе:

×	0	1
0	0	0
1	0	1

Умножение в восьмеричной системе:

×	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	52	61

Умножение в шестнадцатеричной системе:

+	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C
A	0	A	14	1E	28	32	3C	46	50	5A	64
B	0	B	16	21	2C	37	42	4D	58	63
C	0	C	18	24	30	3C	48	54	60	6C
D	0	D	1A	27	34	41	4E	5B	68
E	0	E	1C	2A	38	46	54	62	70
F	0	F	1E	2D	3C	4B	5A	69	78

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример 1. Перемножим числа 5 и 6 (одноразрядные числа перемножают, находя нужное значение из соответствующих таблиц умножения):

Десятичная: 510 × 610 = 3010	Двоичная: 1012 × 1102 = 111102
(из таблиц перемножения)
Восьмеричная: 58 × 68 = 368	Шестнадцатеричная: 516 × 616 = 1E16
(из таблиц перемножения)	(из таблиц перемножения)

Ответ: 5 × 6 = 30₁₀ = 11110₂ = 36₈ = 1E₁₆ .

Проверка. Преобразуем полученные произведения к десятичному виду:

11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;

36₈ = 3_8¹ + 6_8⁰ = 30.

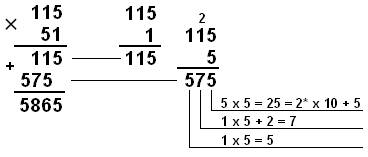
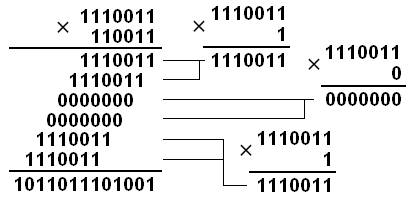
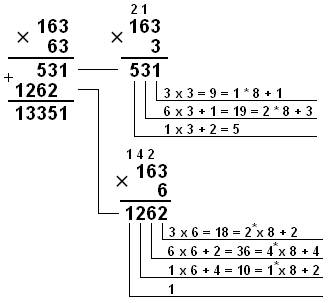
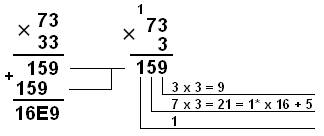
Пример 2. Перемножим числа 115 и 51:

Десятичная: 11510 × 5110 = 586510	Двоичная: 11100112 × 1100112 = 10110111010012
Восьмеричная: 1638 × 638 = 133518	Шестнадцатеричная: 7316 × 3316 = 16E916

* - переносы в следующий разряд

Ответ: 115 × 51 = 5865₁₀ = 1011011101001₂ = 13351₈ = 16E9₁₆ .

Проверка. Преобразуем полученные произведения к десятичному виду:

1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;

13351₈ = 1 ^. 8⁴ + 3 ^. 8³ + 3 ^. 8² + 5 ^. 8¹ + 1 ^. 8⁰ = 5865;

16E9₁₆ = 1 ^. 16³ + 6 ^. 16² + E(14) ^. 16¹ + 9 ^. 16⁰ = 5865.