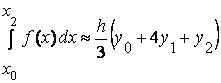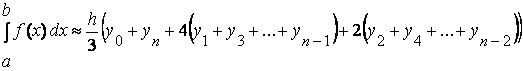1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

1. 3. Метод парабол (метод Симпсона)

Это наиболее широко известный и применяемый метод численного интегрирования.

Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола (рис. 1.3).

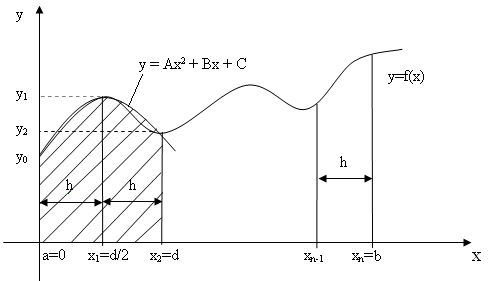
Рис (1.3)

Формулу Симпсона выведем, проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.

.

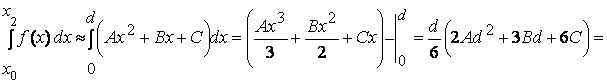
Действительно, определяя y₀, y₁, y₂:

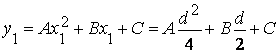
имеем

,

т.е.

(1.5)

окончательно:

или

(1.6)

Последняя формула (1.6) называется формулой Симпсона.

Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.