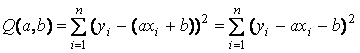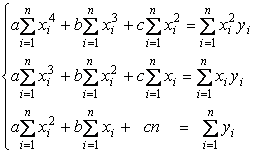3. Аппроксимация
функций с помощью метода
наименьших квадратов
Метод наименьших квадратов применяется при обработке
результатов эксперимента для аппроксимации (приближения) экспериментальных
данных аналитической формулой. Конкретный вид формулы выбирается, как
правило, из физических соображений. Такими формулами могут быть:
![]()
![]()
![]() ,
,
![]()
и
другие.
Сущность метода наименьших квадратов состоит в
следующем. Пусть результаты измерений представлены таблицей:
|
Таблица 4 |
||||
|
x |
x1 |
x2 |
… |
xn |
|
y |
y1 |
y2 |
… |
yn |
Будем
считать, что вид аппроксимирующей (приближающей) зависимости
выбран, и её можно записать в виде
|
|
(3.1) |
где
f -
известная функция, a0, a1, …, am -
неизвестные постоянные параметры, значения которых надо найти. В методе
наименьших квадратов приближение функции (3.1) к экспериментальной зависимости
считается наилучшим, если выполняется условие
|
|
(3.2) |
то
есть суммa квадратов отклонений искомой аналитической функции от
экспериментальной зависимости должна быть минимальна.
Заметим, что функция Q называется невязкой.
Так как невязка
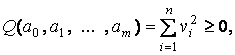
то
она имеет минимум. Необходимым условием минимума функции нескольких переменных
является равенство нулю всех частных производных этой функции по параметрам.
Таким образом, отыскание наилучших значений параметров аппроксимирующей функции
(3.1), то есть таких их значений, при которых Q = Q(a0, a1, …, am) минимальна, сводится к решению системы уравнений:
|
|
(3.3) |
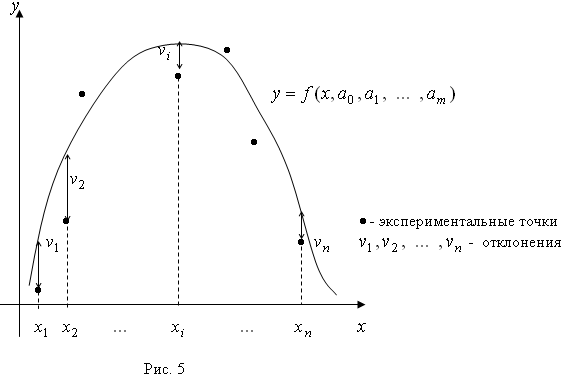
Методу наименьших квадратов можно дать следующее геометрическое
истолкование: среди бесконечного семейства линий данного вида отыскивается одна
линия, для которой сумма квадратов разностей ординат экспериментальных точек и
соответствующих им ординат точек, найденных по уравнению этой линии, будет
наименьшей.
Нахождение параметров линейной функции
Пусть экспериментальные данные надо представить
линейной функцией:
|
|
|
Требуется подобрать такие значения a и b, для которых
функция
|
|
(3.4) |
будет
минимальной. Необходимые условия минимума функции (3.4) сводятся к системе
уравнений:
|
|
|
После
преобразований получаем систему двух линейных уравнений с двумя неизвестными:
|
|
(3.5) |
решая
которую, находим искомые значения параметров a и b.
Нахождение
параметров квадратичной функции
Если аппроксимирующей функцией является квадратичная
зависимость
|
|
|
то
её параметры a, b, c находят из
условия минимума функции:
|
|
(3.6) |
Условия минимума функции (3.6) сводятся к системе
уравнений:
|
|
|
После
преобразований получаем систему трёх линейных уравнений с тремя неизвестными:
|
|
(3.7) |
при
решении которой находим искомые значения
параметров a, b и c.
Пример. Пусть в результате эксперимента получена следующая
таблица значений x и y:
|
Таблица 5 |
||||||||
|
xi |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
|
yi |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
Требуется аппроксимировать экспериментальные данные
линейной и квадратичной функциями.
Решение. Отыскание
параметров аппроксимирующих функций сводится к решению систем линейных
уравнений (3.5) и (3.7). Для решения задачи воспользуемся процессором
электронных таблиц Excel.
1. Сначала сцепим листы 1 и 2. Занесём
экспериментальные значения xi и yi в
столбцы А и В, начиная со второй строки (в первой
строке поместим заголовки столбцов). Затем для этих столбцов вычислим суммы и
поместим их в десятой строке.
В столбцах C – G разместим соответственно вычисление и суммирование
![]()
2. Расцепим листы.
Дальнейшие вычисления проведём аналогичным образом для линейной
зависимости на Листе 1 и для
квадратичной зависимости на Листе 2.
3. Под полученной таблицей сформируем матрицу
коэффициентов и вектор-столбец свободных членов. Решим систему линейных
уравнений по следующему алгоритму:
![]()
Для вычисления обратной матрицы и перемножения матриц
воспользуемся Мастером функций и функциями МОБР и МУМНОЖ.
4. В блоке ячеек H2:H9 на основе полученных коэффициентов вычислим значения аппроксимирующего
полинома yi выч., в блоке I2:I9 –
отклонения Dyi = yi эксп. - yi выч., в столбце J – невязку:
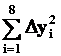
Полученные таблицы и построенные с помощью Мастера
диаграмм графики приведёны на рисунках
6, 7, 8.

Рис. 6. Таблица вычисления коэффициентов линейной
функции,
аппроксимирующей экспериментальные данные.
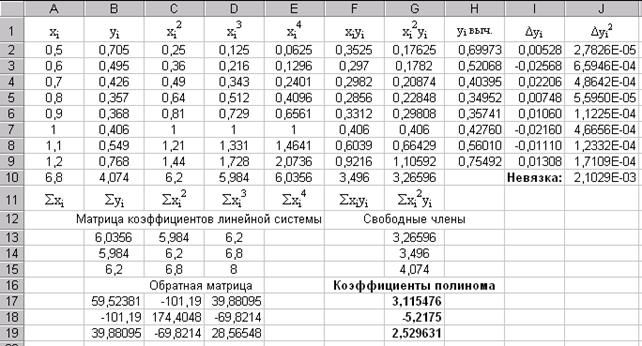
Рис. 7. Таблица вычисления коэффициентов квадратичной
функции,
аппроксимирующей экспериментальные данные.
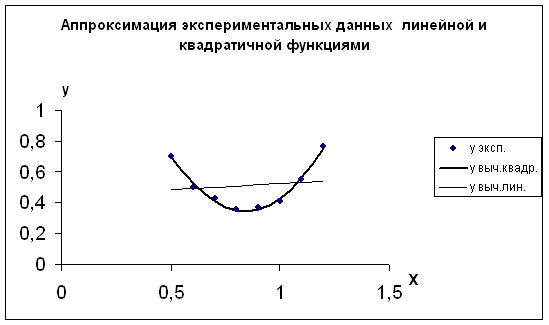
Рис. 8. Графическое представление результатов
аппроксимации
экспериментальных данных линейной и
квадратичной функциями.
Ответ. Аппроксимировали
экспериментальные данные линейной зависимостью y = 0,07881x + 0,442262 c невязкой Q = 0,165167
и квадратичной зависимостью y = 3,115476x2 – 5,2175x +
2,529631 c невязкой Q = 0,002103.
Задания. Аппроксимировать функцию, заданную таблично, линейной
и квадратичной функциями.
|
Таблица 6 |
|||||||||
|
№0 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№1 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
|
|
№2 |
x |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
26 |
2,7 |
|
y |
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
|
|
№3 |
x |
0,3 |
0,6 |
0,9 |
1,2 |
1,5 |
1,8 |
2,1 |
2,4 |
|
y |
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
|
|
№4 |
x |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
2,2 |
2,4 |
2,6 |
|
y |
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
|
|
№5 |
x |
2,1 |
2,3 |
2,5 |
2,7 |
2,9 |
3,1 |
3,3 |
3,5 |
|
y |
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
|
|
№6 |
x |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
2,1 |
2,2 |
|
y |
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
|
|
№7 |
x |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
|
y |
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
|
|
№8 |
x |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
|
y |
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
|
|
№9 |
x |
0,5 |
0,7 |
0,9 |
1,1 |
1,3 |
1,5 |
1,7 |
1,9 |
|
y |
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
4,771 |
|