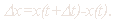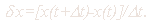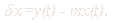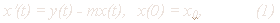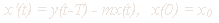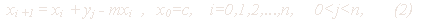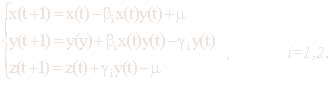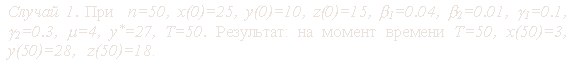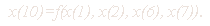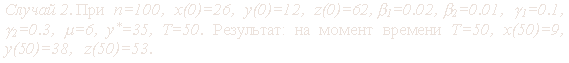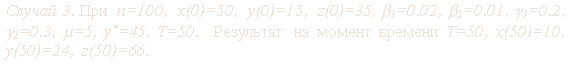Модель - объект или описание объекта, системы для замещения (при
определенных условиях предложениях, гипотезах) одной системы (т.е.
оригинала) другой системы для изучения оригинала или воспроизведения его
каких - либо свойств. Модель - результат отображения одной структуры на
другую. Отображая физическую систему (объект) на математическую
систему (например, математический аппарат уравнений) получим физико -
математическую модель системы или математическую модель физической
системы. В частности, физиологическая система - система кровообращения
человека, подчиняется некоторым законам термодинамики и описав эту
систему на физическом (термодинамическом) языке получим физическую,
термодинамическую модель физиологической системы. Если записать эти
законы на математическом языке, например, выписать соответствующие
термодинамические уравнения, то получим математическую модель системы
кровообращения. Эту модель можно назвать физиолого - физико -
математической моделью или физико - математической моделью.
Модель - объект или описание объекта, системы для замещения (при
определенных условиях предложениях, гипотезах) одной системы (т.е.
оригинала) другой системы для изучения оригинала или воспроизведения его
каких - либо свойств. Модель - результат отображения одной структуры на
другую. Отображая физическую систему (объект) на математическую
систему (например, математический аппарат уравнений) получим физико -
математическую модель системы или математическую модель физической
системы. В частности, физиологическая система - система кровообращения
человека, подчиняется некоторым законам термодинамики и описав эту
систему на физическом (термодинамическом) языке получим физическую,
термодинамическую модель физиологической системы. Если записать эти
законы на математическом языке, например, выписать соответствующие
термодинамические уравнения, то получим математическую модель системы
кровообращения. Эту модель можно назвать физиолого - физико -
математической моделью или физико - математической моделью.
 Модели, если отвлечься от областей, сфер их применения, бывают трех
типов: познавательные, прагматические и инструментальные.
Модели, если отвлечься от областей, сфер их применения, бывают трех
типов: познавательные, прагматические и инструментальные.
 Познавательная модель - форма организации и представления знаний,
средство соединение новых и старых знаний. Познавательная модель, как
правило, подгоняется под реальность и является теоретической моделью.
Познавательная модель - форма организации и представления знаний,
средство соединение новых и старых знаний. Познавательная модель, как
правило, подгоняется под реальность и является теоретической моделью.
 Прагматическая модель - средство организации практических действий,
рабочего представления целей системы для ее управления. Реальность в них
подгоняется под некоторую прагматическую модель. Это, как правило,
прикладные модели.
Прагматическая модель - средство организации практических действий,
рабочего представления целей системы для ее управления. Реальность в них
подгоняется под некоторую прагматическую модель. Это, как правило,
прикладные модели.
 Инструментальная модель - является средством построения,
исследования и/или использования прагматических и/или познавательных
моделей.
Инструментальная модель - является средством построения,
исследования и/или использования прагматических и/или познавательных
моделей.
 Познавательные отражают существующие, а прагматические - хоть и не
существующие, но желаемые и, возможно, исполнимые отношения и связи.
Познавательные отражают существующие, а прагматические - хоть и не
существующие, но желаемые и, возможно, исполнимые отношения и связи.
 По уровню, "глубине" моделирования модели бывают эмпирические - на
основе эмпирических фактов, зависимостей, теоретические - на основе
математических описаний и смешанные, полуэмпирические - использующие
эмпирические зависимости и математические описания.
По уровню, "глубине" моделирования модели бывают эмпирические - на
основе эмпирических фактов, зависимостей, теоретические - на основе
математических описаний и смешанные, полуэмпирические - использующие
эмпирические зависимости и математические описания.
 Математическая модель М описывающая ситему
S (x1,x2,...,xn; R), имеет
вид: М=(z1,z2,...,zm; Q),
где ziÎZ, i=1,2,...,n, Q, R - множества отношений
над X - множеством входных, выходных сигналов и состояний системы и Z
- множеством описаний, представлений элементов и подмножеств X,
соответственно.
Математическая модель М описывающая ситему
S (x1,x2,...,xn; R), имеет
вид: М=(z1,z2,...,zm; Q),
где ziÎZ, i=1,2,...,n, Q, R - множества отношений
над X - множеством входных, выходных сигналов и состояний системы и Z
- множеством описаний, представлений элементов и подмножеств X,
соответственно.
 Основные требования к модели: наглядность построения; обозримость
основных его свойств и отношений; доступность ее для исследования или
воспроизведения; простота исследования, воспроизведения; сохранение
информации, содержавшиеся в оригинале (с точностью рассматриваемых
при построении модели гипотез) и получение новой информации.
Основные требования к модели: наглядность построения; обозримость
основных его свойств и отношений; доступность ее для исследования или
воспроизведения; простота исследования, воспроизведения; сохранение
информации, содержавшиеся в оригинале (с точностью рассматриваемых
при построении модели гипотез) и получение новой информации.
Проблема моделирования состоит из трех задач:
- построение модели (эта задача менее формализуема и конструктивна, в
том смысле, что нет алгоритма для построения моделей);
- исследование модели (эта задача более формализуема, имеются методы
исследования различных классов моделей);
- использование модели (конструктивная и конкретизируемая задача).
 Модель М называется статической, если среди xi нет временного
параметра t. Статическая модель в каждый момент времени дает лишь
"фотографию" сиcтемы, ее срез.
Модель М называется статической, если среди xi нет временного
параметра t. Статическая модель в каждый момент времени дает лишь
"фотографию" сиcтемы, ее срез.
 Модель - динамическая, если среди xi есть временной параметр, т.е.
она отображает систему (процессы в системе) во времени.
Модель - динамическая, если среди xi есть временной параметр, т.е.
она отображает систему (процессы в системе) во времени.
 Модель - дискретная, если она описывает поведение системы только в
дискретные моменты времени.
Модель - дискретная, если она описывает поведение системы только в
дискретные моменты времени.
 Модель - непрерывная, если она описывает поведение системы для всех
моментов времени из некоторого промежутка времени.
Модель - непрерывная, если она описывает поведение системы для всех
моментов времени из некоторого промежутка времени.
 Модель - имитационная, если она предназначена для испытания или
изучения, проигрывания возможных путей развития и поведения объекта
путем варьирования некоторых или всех параметров xi модели М.
Модель - имитационная, если она предназначена для испытания или
изучения, проигрывания возможных путей развития и поведения объекта
путем варьирования некоторых или всех параметров xi модели М.
 Модель - детерминированная, если каждому входному набору
параметров соответствует вполне определенный и однозначно определяемый
набор выходных параметров; в противном случае - модель
недетерминированная, стохастическая (вероятностная).
Модель - детерминированная, если каждому входному набору
параметров соответствует вполне определенный и однозначно определяемый
набор выходных параметров; в противном случае - модель
недетерминированная, стохастическая (вероятностная).
 Можно говорить о различных режимах использования моделей - об
имитационном режиме, о стохастическом режиме и т. д.
Можно говорить о различных режимах использования моделей - об
имитационном режиме, о стохастическом режиме и т. д.
 Модель включает в себя: объект О, субъект (не обязательный) А, задачу
Z, ресурсы B, среду моделирования С: М=.
Модель включает в себя: объект О, субъект (не обязательный) А, задачу
Z, ресурсы B, среду моделирования С: М=.
Свойства любой модели таковы:
- конечность: модель отображает оригинал лишь в конечном числе его
отношений и, кроме того, ресурсы моделирования конечны;
- упрощенность: модель отображает только существенные стороны объекта;
- приблизительность: действительность отображается моделью грубо или
приблизительно;
- адекватность: модель успешно описывает моделируемую систему;
- информативность: модель должна содержать достаточную информацию о
системе - в рамках гипотез, принятых при построении модели.
Жизненный цикл моделируемой системы:
- Сбор информации об объекте, выдвижение гипотез, предмодельный анализ;
- Проектирование структуры и состава моделей (подмоделей);
- Построение спецификаций модели, разработка и отладка отдельных
подмоделей, сборка модели в целом, идентификация (если это нужно)
параметров моделей;
- Исследование модели - выбор метода исследования и разработка алгоритма
(программы) моделирования;
- Исследование адекватности, устойчивости, чувствительности модели;
- Оценка средств моделирования (затраченных ресурсов);
- Интерпретация, анализ результатов моделирования и установление
некоторых причинно - следственных связей в исследуемой системе;
- Генерация отчетов и проектных (народно - хозяйственных) решений;
- Уточнение, модификация модели, если это необходимо, и возврат к
исследуемой системе с новыми знаниями, полученными с помощью
моделирования.
Основными операциями используемыми над моделями являются:
- Линеаризация. Пусть М=М(X,Y,A), где X - множество входов, Y -
выходов, А - состояний системы. Схематически можно это изобразить:
X ® A
® Y
Если X, Y, A - линейные пространства (множества),
а j, y - линейные
операторы, то система (модель) называется линейной. Другие системы
(модели) - нелинейные. Нелинейные системы трудно поддаются исследованию,
поэтому их часто линеаризуют - сводят к линейным каким-то образом.
- Идентификация. Пусть М=М(X,Y,A),
A={ai }, ai=(ai1,ai2,...,aik) - вектор
состояния объекта (системы). Если вектор ai зависит от некоторых
неизвестных параметров, то задача идентификации (модели, параметров
модели) состоит в определении по некоторым дополнительным условиям,
например, экспериментальным данным, характеризующим состояние системы
в некоторых случаях. Идентификация - решение задачи построения по
результатам наблюдений математических моделей, описывающих адекватно
поведение реальной системы.
- Агрегирование. Операция состоит в преобразовании (сведении) модели
к модели (моделям) меньшей размерности (X, Y, A).
- Декомпозиция. Операция состоит в разделении системы (модели) на
подсистемы (подмодели) с сохранением структур и принадлежности одних
элементов и подсистем другим.
- Сборка. Операция состоит в преобразовании системы, модели,
реализующей поставленную цель из заданных или определяемых подмоделей
(структурно связанных и устойчивых).
- Макетирование. Эта операция состоит в апробации, исследовании
структурной связности, сложности, устойчивости с помощью макетов или
подмоделей упрощенного вида, у которых функциональная часть упрощена
(хотя вход и выход подмоделей сохранены).
- Экспертиза, экспертное оценивание. Операция или процедура
использования опыта, знаний, интуиции, интеллекта экспертов для
исследования или моделирования плохо структурируемых, плохо
формализуемых подсистем исследуемой системы.
- Вычислительный эксперимент. Это эксперимент, осуществляемый с
помощью модели на ЭВМ с целью распределения, прогноза тех или иных
состояний системы, реакции на те или иные входные сигналы. Прибором
эксперимента здесь является компьютер (и модель!).
 Модели и моделирование применяются по следующим основным и
важным направлениям.
Модели и моделирование применяются по следующим основным и
важным направлениям.
- Обучение (как моделям, моделированию, так и самих моделей).
- Познание и разработка теории исследуемых систем - с помощью
каких - то моделей, моделирования, результатов моделирования.
- Прогнозирование (выходных данных, ситуаций, состояний системы).
- Управление (системой в целом, отдельными подсиситемами системы,
выработка управленческих решений и стратегий).
- Автоматизация (системы или отдельных подсистем системы).
 В базовой четверке информатики: "модель - алгоритм - компьютер -
технология" при компьютерном моделировании главную роль играют уже
алгоритм (программа), компьютер и технология (точнее, инструментальные
системы для компьютера, компьютерные технологии).
В базовой четверке информатики: "модель - алгоритм - компьютер -
технология" при компьютерном моделировании главную роль играют уже
алгоритм (программа), компьютер и технология (точнее, инструментальные
системы для компьютера, компьютерные технологии).
 Например, при имитационном моделировании (при отсутствии строгого и
формально записанного алгоритма) главную роль играют технология и
средства моделирования; аналогично и в когнитивной графике.
Например, при имитационном моделировании (при отсутствии строгого и
формально записанного алгоритма) главную роль играют технология и
средства моделирования; аналогично и в когнитивной графике.
Основные функции компьютера при моделировании систем:
- выполнять роль вспомогательного средства для решения задач, решаемых
обычными вычислительными средствами, алгоритмами, технологиями;
- выполнять роль средства постановки и решения новых задач, не решаемых
традиционными средствами, алгоритмами, технологиями;
- выполнять роль средства конструирования компьютерных обучающе -
моделирующих сред;
- выполнять роль средства моделирования для получения новых знаний;
- выполнять роль "обучения" новых моделей (самообучающиеся модели).
 Компьютерное моделирование - основа представления знаний в ЭВМ
(построения различных баз знаний). Компьютерное моделирование для
рождения новой информации использует любую информацию, которую
можно актуализировать с помощью ЭВМ.
Компьютерное моделирование - основа представления знаний в ЭВМ
(построения различных баз знаний). Компьютерное моделирование для
рождения новой информации использует любую информацию, которую
можно актуализировать с помощью ЭВМ.
 Разновидностью компьютерного моделирования является
вычислительный эксперимент.
Разновидностью компьютерного моделирования является
вычислительный эксперимент.
 Компьютерное моделирование, вычислительный эксперимент становится
новым инструментом, методом научного познания, новой технологией также
из-за возрастающей необходимости перехода от исследования линейных
математических моделей систем .
Компьютерное моделирование, вычислительный эксперимент становится
новым инструментом, методом научного познания, новой технологией также
из-за возрастающей необходимости перехода от исследования линейных
математических моделей систем .
 Компьютерное моделирование, от постановки задачи - до получения
результатов, проходит следующие этапы.
Компьютерное моделирование, от постановки задачи - до получения
результатов, проходит следующие этапы.
- Постановка задачи.
- Формулировка задачи.
- Определение цели моделирования и их приоритетов.
- Сбор информации о системе, объекте моделирования.
- Описание данных (их структуры, диапазона, источника и т. д.).
- Предмодельный анализ.
- Анализ существующих аналогов и подсистем.
- Анализ технических средств моделирования (ЭВМ, периферия).
- Анализ программного обеспечения(языки программирования, пакеты
программ, инструментальные среды).
- Анализ математического обеспечения(модели, методы, алгоритмы).
- Анализ задачи (модели).
- Разработка структур данных.
- Разработка входных и выходных спецификаций, форм представления
данных.
- Проектирование структуры и состава модели (подмоделей).
- Исследование модели.
- Выбор методов исследования подмоделей.
- Выбор, адаптация или разработка алгоритмов, их псевдокодов.
- Сборка модели в целом из подмоделей.
- Идентификация модели, если в этом есть необходимость.
- Формулировка используемых критериев адекватности, устойчивости
и чувствительности модели.
- Программирование (проектирование программы).
- Выбор метода тестирования и тестов (контрольных примеров).
- Кодирование на языке программирования(написание команд).
- Комментирование программы.
- Тестирование и отладка.
- Синтаксическая отладка.
- Семантическая отладка (отладка логической структуры).
- Тестовые расчеты, анализ результатов тестирования.
- Оптимизация программы.
- Оценка моделирования.
- Оценка средств моделирования.
- Оценка адекватности моделирования.
- Оценка чувствительности модели.
- Оценка устойчивости модели.
- Документирование.
- Описание задачи, целей.
- Описание модели, метода, алгоритма.
- Описание среды реализации.
- Описание возможностей и ограничений.
- Описание входных и выходных форматов, спецификаций.
- Описание тестирования.
- Описание инструкций пользователю.
- Сопровождение.
- Анализ использования, периодичности использования, количества
пользователей, типа использования (диалог, автономно и др.), анализ отказов
во время использования модели.
- Обслуживание модели, алгоритма, программы и их эксплуатация.
- Расширение возможностей: включение новых функций или
изменение режимов моделирования, в том числе и под модифицированную
среду.
- Нахождение, исправление скрытых ошибок в программе, если
таковые найдутся.
- Использование модели.
4.2. Модели и моделирование систем
Математическое и компьютерное моделирование.
 Данный период
характерен необходимостью моделирования различных социально-
экономических процессов и систем и принятия решений на основе результатов
моделирования, ибо такие системы и процессы достаточно сложны,
многогранны, динамичны, подвержены случайным воздействиям. Достаточно
интенсивно моделируются сейчас такие социально-экономические процессы,
как демографические (например, эволюция и цикличность), социальные
(например, поведение социальных групп, социальных последствий тех или
иных решений), экономические (например, рыночные отношения, налоговые
сборы, риски), гуманитарные (например, воздействие на человека
информационного потока) и др. Приведём пример математического
моделирования некоторой системы (полный жизненный цикл
моделирования).Решение поставленной задачи разобьем на этапы, в
соответствии с этапами жизненного цикла моделирования, объединяя для
удобства некоторые этапы для удобства и краткости изложения.
Данный период
характерен необходимостью моделирования различных социально-
экономических процессов и систем и принятия решений на основе результатов
моделирования, ибо такие системы и процессы достаточно сложны,
многогранны, динамичны, подвержены случайным воздействиям. Достаточно
интенсивно моделируются сейчас такие социально-экономические процессы,
как демографические (например, эволюция и цикличность), социальные
(например, поведение социальных групп, социальных последствий тех или
иных решений), экономические (например, рыночные отношения, налоговые
сборы, риски), гуманитарные (например, воздействие на человека
информационного потока) и др. Приведём пример математического
моделирования некоторой системы (полный жизненный цикл
моделирования).Решение поставленной задачи разобьем на этапы, в
соответствии с этапами жизненного цикла моделирования, объединяя для
удобства некоторые этапы для удобства и краткости изложения.
Этап 1. Содержательная постановка задачи
 Современное производство характеризуется тем, что некоторая часть
производимой продукции (в стоимостном выражении) возвращается в виде
инвестиций (т.е. части конечной продукции, используемой для создания
основных фондов производства) в производство. При этом время возврата,
ввода в оборот новых фондов может быть различной для различного рода
производства. Необходимо промоделировать данную эту ситуацию и выявить
динамику изменения величины основных фондов производства (капитала).
Современное производство характеризуется тем, что некоторая часть
производимой продукции (в стоимостном выражении) возвращается в виде
инвестиций (т.е. части конечной продукции, используемой для создания
основных фондов производства) в производство. При этом время возврата,
ввода в оборот новых фондов может быть различной для различного рода
производства. Необходимо промоделировать данную эту ситуацию и выявить
динамику изменения величины основных фондов производства (капитала).
 Сложность и многообразие, слабая структурированность и плохая
формализуемость основных экономических механизмов, определяющих
работу предприятий не позволяют преобразовать процедуры принятия
решений в экономической системе в полностью эффективные математические
модели и алгоритмы прогнозирования. Поэтому часто эффективно
использование простых, но гибких и надёжных процедур принятия решения.
Сложность и многообразие, слабая структурированность и плохая
формализуемость основных экономических механизмов, определяющих
работу предприятий не позволяют преобразовать процедуры принятия
решений в экономической системе в полностью эффективные математические
модели и алгоритмы прогнозирования. Поэтому часто эффективно
использование простых, но гибких и надёжных процедур принятия решения.
 Рассмотрим одну такую простую модель. Эта модель будет полезна для
прогноза событий и связанных с ними социально-экономических процессов.
Рассмотрим одну такую простую модель. Эта модель будет полезна для
прогноза событий и связанных с ними социально-экономических процессов.
Этап 2. Формулировка гипотез, построение, исследование модели
 Структура производства и сбыта часто зависит от изменений в
окружающей среде (социально-экономических условий).
Структура производства и сбыта часто зависит от изменений в
окружающей среде (социально-экономических условий).
 Динамика изменения величины капитала определяется, в основном, в
нашей модели, простыми процессами производства и описывается так
называемыми обобщенными коэффициентами амортизации (расхода фондов)
и потока инвестиций (часть конечного продукта, используемого в единицу
времени для создания основных фондов). Эти коэффициенты - относительные
величины (за единицу времени). Необходимо разработать и исследовать
модель динамики основных фондов. Считаем при этом допустимость
определённых гипотез, определяющих рассматриваемую систему
производства.
Динамика изменения величины капитала определяется, в основном, в
нашей модели, простыми процессами производства и описывается так
называемыми обобщенными коэффициентами амортизации (расхода фондов)
и потока инвестиций (часть конечного продукта, используемого в единицу
времени для создания основных фондов). Эти коэффициенты - относительные
величины (за единицу времени). Необходимо разработать и исследовать
модель динамики основных фондов. Считаем при этом допустимость
определённых гипотез, определяющих рассматриваемую систему
производства.
 Пусть x(t) - величина основных фондов (капитала) в момент времени t,
где 0 £ t £ N.
Через промежуток времени Dt она будет равна x(t+Dt).
Пусть x(t) - величина основных фондов (капитала) в момент времени t,
где 0 £ t £ N.
Через промежуток времени Dt она будет равна x(t+Dt).
Абсолютный прирост равен
Относительный прирост будет равен
Примем следующие гипотезы:
- социально-экономические условия производства достаточно хорошие и
способствуют росту производства, а поток инвестиций задается в виде
известной функции y(t);
- коэффициент амортизации фондов считается неизменным и равным m и
при достаточно малом Dt изменение основных фондов прямо
пропорционально текущей величине капитала, т.е.
 Считая Dt ® 0,
а также учитывая определение производной, получим из
предыдущего соотношения следующее математическое выражение закона
изменения величины капитала - математическую модель (уравнение) динамики
капитала (такие уравнения называются дифференциальными):
Считая Dt ® 0,
а также учитывая определение производной, получим из
предыдущего соотношения следующее математическое выражение закона
изменения величины капитала - математическую модель (уравнение) динамики
капитала (такие уравнения называются дифференциальными):
где х(0) - начальное значение капитала в момент времени t=0.
 Эта величина х0 везде в дальнейшем будет считаться заданной. Эта
простейшая модель динамики величины капитала.
Эта величина х0 везде в дальнейшем будет считаться заданной. Эта
простейшая модель динамики величины капитала.
 Эта простейшая модель не отражает того факта, что социально-
экономические ресурсы производства таковы, что между выделением
инвестиций и их введением и использованием в выпуске новой продукции
проходит некоторое время - лаг. Учитывая это можно записать модель (1) в
виде:
Эта простейшая модель не отражает того факта, что социально-
экономические ресурсы производства таковы, что между выделением
инвестиций и их введением и использованием в выпуске новой продукции
проходит некоторое время - лаг. Учитывая это можно записать модель (1) в
виде:
 Данной непрерывной, дифференциальной, динамической модели можно
поставить в соответствие простую дискретную модель:
Данной непрерывной, дифференциальной, динамической модели можно
поставить в соответствие простую дискретную модель:
где n - предельное значение момента времени при моделировании.
Эта дискретная модель получается из непрерывной при Dt=1, а также
заменой производной x'(t) на относительное приращение
Dt (замена, как это
следует из определения производной, справедлива при малых
Dt).
Этап 3. Построение алгоритма и программы моделирования
 Рассмотрим для простоты режим моделирования когда
m, c, y - известны
и постоянны, а также рассмотрим наиболее простой алгоритм моделирования
в укрупнённых шагах.
Рассмотрим для простоты режим моделирования когда
m, c, y - известны
и постоянны, а также рассмотрим наиболее простой алгоритм моделирования
в укрупнённых шагах.
- Ввод входных данных для моделирования:
с=х(0) - начальный капитал;
n - конечное время моделирования;
m - коэффициент амортизации;
s - единица измерения времени;
y - инвестиции.
- Вычисление xi от i=1 до i=n по рекуррентной формуле (2).
- Поиск стационарного состояния - такого момента времени j,
0<=j<=n, начиная
с которого все хj, хj+1,...,хn постоянны или изменяются на малую
допустимую величину e>0.
- Выдача результатов моделирования и, по желанию пользователя, графика.
 Приведём программу на Паскале для имитационного моделирования
(компактность программы «принесена в жертву» структурированности).
Приведём программу на Паскале для имитационного моделирования
(компактность программы «принесена в жертву» структурированности).
PROGRAM MODFOND;
{Исходные данные находятся в файле in.dat текущего каталога}
{Результаты записываются в файл out.dat текущего каталога}
Uses
Crt, Graph, Textwin;
Type
Vector = Array[0..2000] of Real;
Mas = Array[0..2000] of LongInt;
Var
Time,Lag,t,dv,mv,i,yi,p : Integer;
tmax,tmin : LongInt;
a,b,m,X0,maxx,minx,aa,bb,cc,sx,tk : Real;
x : Vector;
ax,ay : Mas;
ch : Char;
f1,f2 : Text;
{----------------------------------------------------------------------------}
Procedure InputKeyboard; { Ввод с клавиатуры }
Begin
OpenWindow(10,5,70,20,' Ввод данных ',14,4);
ClrScr; WriteLn; WriteLn('Введите время Т прогнозирования системы:');
Repeat
Writeln('Для удобства построения графика введите Т не меньше 2');
Write('Т ='); ReadLn(Time);
until Time>=2;
WriteLn('Введите лаг:');
Repeat
Write('Лаг должен быть строго меньше Т - '); ReadLn(Lag);
until Lag0 ) a = '); ReadLn(a);
Write('( b>0 ) b = '); ReadLn(b);
Repeat
Write('Введите коэффициент амортизации ( 0 < M < 1 ) - '); Readln(m);
until (m<1) and (m>0);
Write('Введите значение фондов в начальный момент - '); Readln(X0);
CloseWindow;
end;
{----------------------------------------------------------------------------}
Procedure InputFile; { Ввод из файла }
Begin
Assign(f1,'in.dat'); Reset(f1);
Readln(f1,time,lag,a,b,m,X0); Close(f1);
End;
{----------------------------------------------------------------------------}
Procedure OutputFile; { Запись результата работы в файл }
Begin
Assign(f2,'out.dat'); Rewrite(f2);
WriteLn(f2,' Результаты моделирования:');
WriteLn(f2,'Значение фондов в заданное время Т = ',x[time]:4:2);
WriteLn(f2,'Максимальное значение фондов = ',maxx:4:2);
Write(f2,'Минимальное значение фондов = ',minx:4:2);
Close(f2);
End;
{----------------------------------------------------------------------------}
Procedure InputRnd; { Ввод случайными числами }
Begin
Randomize;
Repeat Time:=Random(90); until Time>=2;
Repeat Lag:=Random(80); until Lagmaxx
then begin maxx:=x[t]; tmax:=t; end
else if x[t]'); OutTextXY(67,47,'^'); OutTextXY(57,415,'0');
OutTextXY(80,45,'X(T) - (Величина основных фондов производства)');
OutTextXY(590,415,'T'); OutTextXY(540,430,'(Время)'); SetColor(2);
For i:=1 to 16 do Line(67,70+20*i,70,70+20*i);
For i:=1 to 24 do Line(70+20*i,410,70+20*i,413);
Mas_OX; Mas_OY;
For t:=0 to time do
Вegin
SetColor(Blue); Circle(ax[t],ay[t],2);
SetFillStyle(SolidFill,Red); FloodFill(ax[t],ay[t],Blue);
End;
SetColor(Red); SetLineStyle(3,1,1);
Line(70,ay[time],ax[time],ay[time]);
Line(ax[time],ay[time],ax[time],410);
Ipol(0,x[0],1,x[1],2,x[2]);
For i:=ax[0] to ax[2] do
Begin
sx:=p*(i-70)/20;
yi:=410-round(20*(aa*sx*sx+bb*sx+cc)/tk);
SetColor(Red); Circle(i,yi,1);
End;
For t:=1 to Time-2 do
Begin
Ipol(t,x[t],t+1,x[t+1],t+2,x[t+2]);
For i:=ax[t+1] to ax[t+2] do
Begin
sx:=p*(i-70)/20;
yi:=410-round(20*(aa*sx*sx+bb*sx+cc)/tk);
SetColor(Red); Circle(i,yi,1);
End;
End;
ReadKey; CloseGraph;
End;
{----------------------------------------------------------------------------}
Begin
While true do
Begin
ClrScr; TextBackGround(2); Window(1,1,80,25); ClrScr;
OpenWindow(30,22,50,24,' Нажмите клавишу... ',4,1);
OpenWindow(5,5,75,16,' Динамика фондов производства ',14,5);
ClrScr; WriteLn;
WriteLn(' Пусть х(t) - основные фонды в момент времени t, y(t) -');
WriteLn(' инвестиции, m - коэффициент амортизации фондов.');
WriteLn(' Модель динамики основных фондов (L - лаг):');
Write(' x`(t) = y(t-L) - mx(t), где х(0) = Хо, y(t)=at+b, ( a,b>0 ).');
ReadKey; CloseWindow;
OpenWindow(15,10,65,17,' Выбирите вариант ввода: ',15,0);
ClrScr; WriteLn;
WriteLn(' С клавиатуры - < 1 >');
WriteLn(' Из файла - < 2 >');
WriteLn(' Случайными числами - < 3 >');
WriteLn(' Выход - ');
ch:=ReadKey;
Сase ch of
#49: InputKeyboard;
#50: Вegin InputFile; OutputScreen; Еnd;
#51: Вegin InputRnd; OutputScreen; End;
#27: Halt(1);
End;
CloseWindow; Worker; OutputFile; OpenWindow(22,10,58,14,'',15,5);
ClrScr; WriteLn;
Write('Для просмотра графика нажмите ввод'); ch:=ReadKey;
If ch=#13 then begin Graf; RestoreCrtMode; end;
CloseWindow; TextBackGround(15); Window(1,1,80,25);
ClrScr; OpenWindow(15,10,65,16,'',15,6); ClrScr; WriteLn;
WriteLn(' Хотите еще моделировать ?'); WriteLn;
WriteLn('Для выхода нажмите - < Esc >');
WriteLn('Для продолжения нажмите любую другую клавишу');
ch:=ReadKey;
If ch=#27 then Halt(1);
CloseWindow;
End;
ClrScr; TextBackGround(0);
End.
Этап 4. Проведение вычислительных экспериментов
 Эксперимент 1. Поток инвестиций постоянный и в каждый момент
времени равен 111. В начальный момент капитал - 1000 руб. Коэффициент
амортизации - 0.0025. Построить модель динамики (посуточно) и найти
величину основных фондов через 50 суток, если лаг равен 10 суток.
Эксперимент 1. Поток инвестиций постоянный и в каждый момент
времени равен 111. В начальный момент капитал - 1000 руб. Коэффициент
амортизации - 0.0025. Построить модель динамики (посуточно) и найти
величину основных фондов через 50 суток, если лаг равен 10 суток.
 Эксперимент 2. Основные фонды в момент времени t=0 была равны
50000. Через какое время общая их сумма превысит 1200000 руб., если поток
инвестиций постоянный и равен 200, а m=0.02, T=5?
Эксперимент 2. Основные фонды в момент времени t=0 была равны
50000. Через какое время общая их сумма превысит 1200000 руб., если поток
инвестиций постоянный и равен 200, а m=0.02, T=5?
Этап 5. Модификация (развитие) модели
 Для модели динамики фондов с переменным законом потока инвестиций:
Для модели динамики фондов с переменным законом потока инвестиций:
а) построить гипотезы, модель и алгоритм моделирования;
б) сформулировать планы вычислительных, компьютерных экспериментов по модели;
в) реализовать алгоритм и планы экспериментов на ЭВМ.
Компьютерное моделирование и вычислительные эксперименты
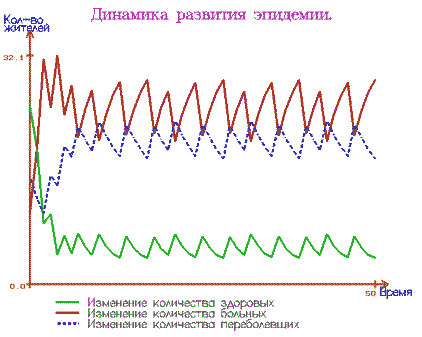
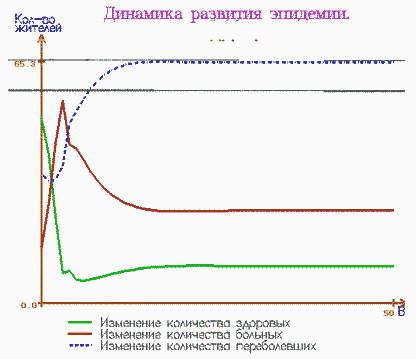
 Рассмотрим следующую модель течения эпидемии. Пусть существует группа
из n контактирующих индивидуумов, в которой в момент времени t имеется
x восприимчивых индивидуумов, y - источников инфекции и z - удаленных
(изолированных или выздоровевших и ставших невосприимчивыми к
инфекции) индивидуумов. Таким образом, имеем: x+y+z=n.
Рассмотрим следующую модель течения эпидемии. Пусть существует группа
из n контактирующих индивидуумов, в которой в момент времени t имеется
x восприимчивых индивидуумов, y - источников инфекции и z - удаленных
(изолированных или выздоровевших и ставших невосприимчивыми к
инфекции) индивидуумов. Таким образом, имеем: x+y+z=n.
 Определим исходные параметры системы:
b — частота контактов между членами группы;
g — частота случаев удаления;
m — скорость пополнения
восприимчивых индивидуумов извне (она же и есть скорость гибели
индивидуумов, удаленных из популяции);
y* — критическое значение, при котором начинается эпидемия.
Определим исходные параметры системы:
b — частота контактов между членами группы;
g — частота случаев удаления;
m — скорость пополнения
восприимчивых индивидуумов извне (она же и есть скорость гибели
индивидуумов, удаленных из популяции);
y* — критическое значение, при котором начинается эпидемия.
 После какой — либо одной вспышки эпидемии, в результате которой
плотность восприимчивых индивидуумов упадет ниже критического значения
y*, наступает период относительного затишья, длящийся до тех пор, пока
снова не будет достигнуто критическое значение y* и не возникнет новая
вспышка. За время Dt
группа восприимчивых индивидуумов, с одной стороны,
уменьшается на b xy Dt
за счет заражения части из них, а с другой — увеличивается на
n Dt.
После какой — либо одной вспышки эпидемии, в результате которой
плотность восприимчивых индивидуумов упадет ниже критического значения
y*, наступает период относительного затишья, длящийся до тех пор, пока
снова не будет достигнуто критическое значение y* и не возникнет новая
вспышка. За время Dt
группа восприимчивых индивидуумов, с одной стороны,
уменьшается на b xy Dt
за счет заражения части из них, а с другой — увеличивается на
n Dt.
 При t=0 заданы x(0)=x0,
y(0)=y0, z(0)=z0 - число восприимчивых,
инфекционных и удаленных индивидуумов соответственно.
При t=0 заданы x(0)=x0,
y(0)=y0, z(0)=z0 - число восприимчивых,
инфекционных и удаленных индивидуумов соответственно.
 Рассматривается промежуток
времени t (0 £ t £ T).
При малых Dt=1 (например, минута) получим соотношения (дискретную модель):
Рассматривается промежуток
времени t (0 £ t £ T).
При малых Dt=1 (например, минута) получим соотношения (дискретную модель):
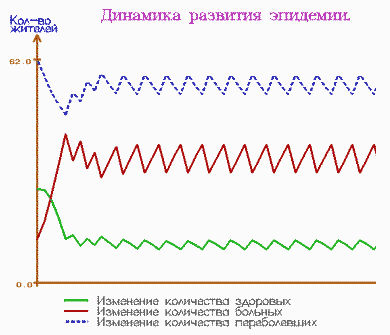
Приведём результаты проведённых вычислительных экспериментов.
 Первые два случая демонстрируют периодичность эпидемии. В
последнем примере имеет место случай стационарного состояния, т.е. после
некоторого момента времени t количества индивидуумов в группах x, y, z
остаются постоянными.
Первые два случая демонстрируют периодичность эпидемии. В
последнем примере имеет место случай стационарного состояния, т.е. после
некоторого момента времени t количества индивидуумов в группах x, y, z
остаются постоянными.
 Программу компьютерного моделирования и вычислительные
эксперименты реализовали студентки математического факультета КБГУ
Буздова Асият и Мильман Евгения.
Программу компьютерного моделирования и вычислительные
эксперименты реализовали студентки математического факультета КБГУ
Буздова Асият и Мильман Евгения.
Компьютерное моделирование.
 Рассмотрим проблему расчета
влажности почвы с учетом накапливаемой биомассы и прогнозирования
урожайности сельхозкультур по заданной (экологически обоснованной)
влагообеспеченности корнеобитаемого слоя почвы. Разработать
соответствующую компьютерную моделирующую среду, которая позволяет
решать задачи прогноза влажности корнеобитаемого слоя почвы и
урожайности (биомассы) сельхозкультур на заданный момент времени с
развитыми интерфейсными средствами, рассчитанными на
неподготовленного пользователя-агронома, эколога и др. Опишем одну
такую программную среду, реализованную реально в среде Delphi 2.0
Windows 95 автором и студентами КБГУ Кирьязевой С.К. и Кирьязевым
Д.А. для расчета влажности почвы и определения урожайности
сельхозкультур. Общение с пользователем осуществляется с помощью
диалогового окна “Расчет влажности и урожайности”, содержащего 5
страниц: “Эксперимент”, “С/х культура”, “Регион”, “Рабочая” и “Результат”.
Рассмотрим проблему расчета
влажности почвы с учетом накапливаемой биомассы и прогнозирования
урожайности сельхозкультур по заданной (экологически обоснованной)
влагообеспеченности корнеобитаемого слоя почвы. Разработать
соответствующую компьютерную моделирующую среду, которая позволяет
решать задачи прогноза влажности корнеобитаемого слоя почвы и
урожайности (биомассы) сельхозкультур на заданный момент времени с
развитыми интерфейсными средствами, рассчитанными на
неподготовленного пользователя-агронома, эколога и др. Опишем одну
такую программную среду, реализованную реально в среде Delphi 2.0
Windows 95 автором и студентами КБГУ Кирьязевой С.К. и Кирьязевым
Д.А. для расчета влажности почвы и определения урожайности
сельхозкультур. Общение с пользователем осуществляется с помощью
диалогового окна “Расчет влажности и урожайности”, содержащего 5
страниц: “Эксперимент”, “С/х культура”, “Регион”, “Рабочая” и “Результат”.
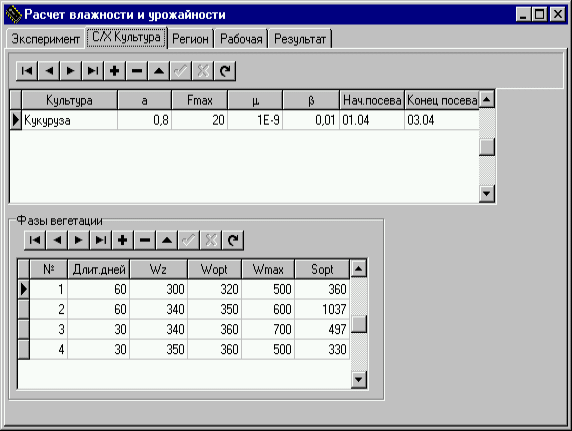
 Страница “С/х культура”- для ввода входной информации по культуре.
Страница “С/х культура”- для ввода входной информации по культуре.
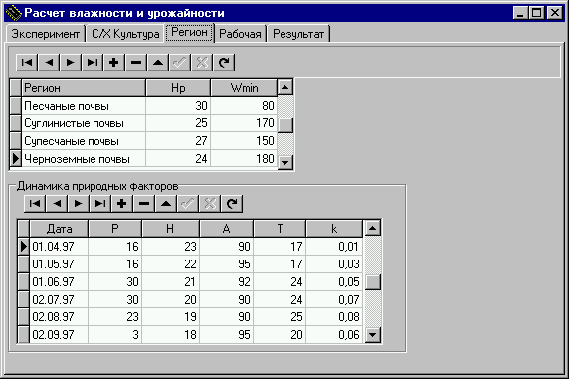
Страница “Регион” - для ввода информации по региону эксперимента.
Страница “Эксперимент” выглядит следующим образом.
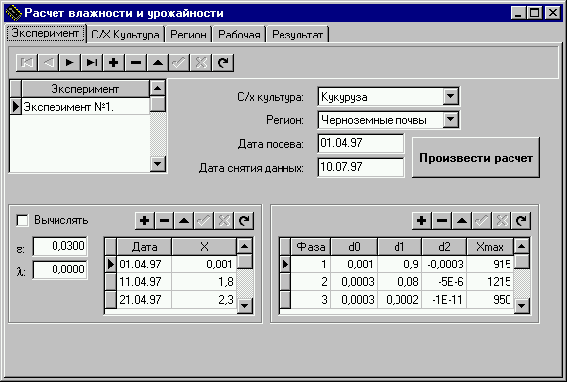
 Данная страница предназначена для ввода названия эксперимента, выбора
названия культуры из списка имеющихся (которые были введены на странице
“С/х культура”), региона проведения эксперимента из списка регионов,
введенных на странице “Регион”, ввода даты посева культуры и даты снятия
урожая, для ввода данных по величинам, зависящим от вида культуры, типа
почв (по фазам вегетации). Предусмотрена возможность выбора: вычислять ли
значения коэффициентов e и l
или же рассматривать их как постоянные
величины? После заполнения страницы “Эксперимент”, можно произвести
расчет влажности почвы и прогноз урожайности культуры. Для этого
достаточно лишь нажать кнопку “Произвести расчет” на странице
“Эксперимент”. После этого автоматически раскрывается страница “Результат”
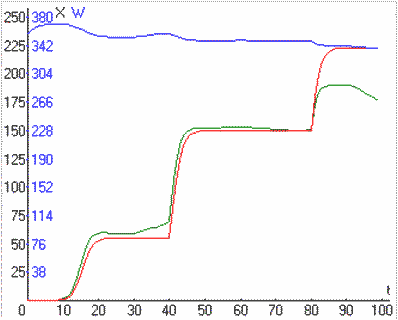
с таблицей рассчитанных величин и выводится график зависимости влажности
почвы от времени (1 - синим цветом), накопления биомассы растений от
времени при вычисленной влажности (2 - зеленым цветом) и оптимального
развития растений - по экспериментальным данным за прошлый год (3 -
красным цветом).
Данная страница предназначена для ввода названия эксперимента, выбора
названия культуры из списка имеющихся (которые были введены на странице
“С/х культура”), региона проведения эксперимента из списка регионов,
введенных на странице “Регион”, ввода даты посева культуры и даты снятия
урожая, для ввода данных по величинам, зависящим от вида культуры, типа
почв (по фазам вегетации). Предусмотрена возможность выбора: вычислять ли
значения коэффициентов e и l
или же рассматривать их как постоянные
величины? После заполнения страницы “Эксперимент”, можно произвести
расчет влажности почвы и прогноз урожайности культуры. Для этого
достаточно лишь нажать кнопку “Произвести расчет” на странице
“Эксперимент”. После этого автоматически раскрывается страница “Результат”
с таблицей рассчитанных величин и выводится график зависимости влажности
почвы от времени (1 - синим цветом), накопления биомассы растений от
времени при вычисленной влажности (2 - зеленым цветом) и оптимального
развития растений - по экспериментальным данным за прошлый год (3 -
красным цветом).
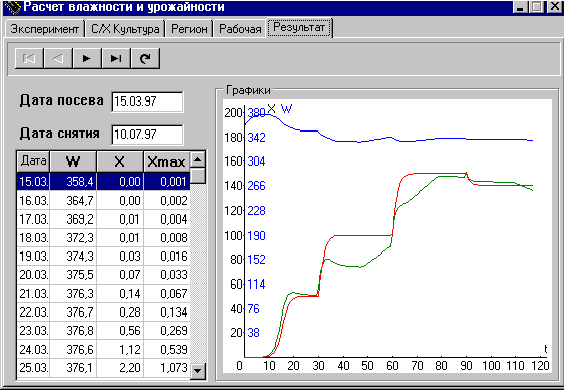
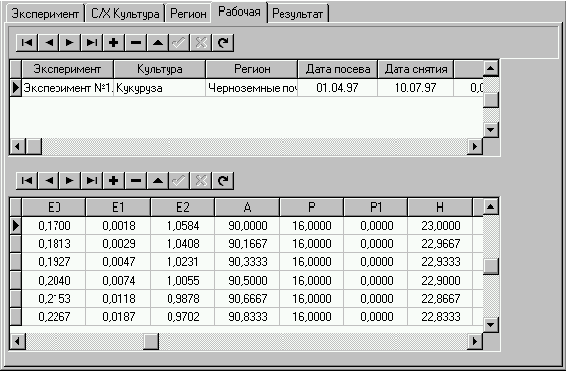
Страница “Рабочая” - для визуального анализа расчётных величин.
 Были проведены вычислительные эксперименты для двух сельхозкультур -
кукурузы и ярового ячменя с использованием общедоступных данных (это
также можно отнести к достоинствам системы). Данные по температуре
воздуха, величине осадков, уровню грунтовых вод и относительной влажности
воздуха представлены с интервалом в 10-15 суток за весь период
вегетационного цикла растения. Программа отображает результаты расчета в
таблице и на графике. График оптимального развития рассматриваемой
культуры имеет “ступенчатый” характер ввиду того, что экспериментально
полученные значения за прошлый год вводятся по фазам вегетации, а для
межфазных периодов программно рассчитываются по соответствующим
математическим моделям. Результаты экспериментов приведены ниже.
Были проведены вычислительные эксперименты для двух сельхозкультур -
кукурузы и ярового ячменя с использованием общедоступных данных (это
также можно отнести к достоинствам системы). Данные по температуре
воздуха, величине осадков, уровню грунтовых вод и относительной влажности
воздуха представлены с интервалом в 10-15 суток за весь период
вегетационного цикла растения. Программа отображает результаты расчета в
таблице и на графике. График оптимального развития рассматриваемой
культуры имеет “ступенчатый” характер ввиду того, что экспериментально
полученные значения за прошлый год вводятся по фазам вегетации, а для
межфазных периодов программно рассчитываются по соответствующим
математическим моделям. Результаты экспериментов приведены ниже.
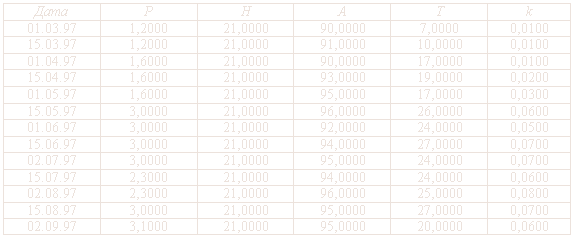
Эксперимент 1
С/х культура: Кукуруза "Луч-300";
Fmax = 20 Дж/(м2сут.); s = 0,6;
m = 10-8; а = 0,8;
Время проведения посева с 01.04. по 20.04.
Тип почвы: Черноземные почвы.
Пороговая величина уровня грунтовых вод: Нр = 24;
Влажность устойчивого завядания: Wmin = 180 мм.
где Р - величина осадков (мм); Н - уровень грунтовых вод (м3/га);
А - относительная влажность воздуха (%); Т - температура воздуха;
k - коэффициент испаряемости на 1оС.
С/х культура: Кукуруза "Луч-300".
Тип почвы: Черноземные почвы.
Дата посева: 02.04.97.
Дата снятия: 10.07.97.
e = 0,0370;
l = 0,0002.
Результаты расчетов - в виде графиков, таблица расчётов не выводится.
Экспертная система.
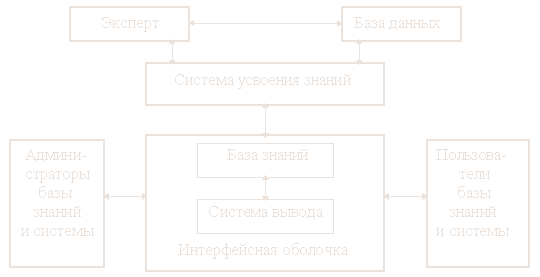
 Спроектируем одну гипотетическую базу знаний
и экспертную систему. Структура базы знаний и экспертной системы
изображена ниже.
Спроектируем одну гипотетическую базу знаний
и экспертную систему. Структура базы знаний и экспертной системы
изображена ниже.
 Экспертная система может рассуждать (имитировать рассуждения) и
настраиваться на предметную область.
Экспертная система может рассуждать (имитировать рассуждения) и
настраиваться на предметную область.
 Рассматривается база знаний и экспертная система “Социально-
экономико - экологическая система”, которая построена (Казиевым В. М. и
студентом КБГУ Тебуевым М. Д.) с использованием аппарата нечётких
множеств и логики и позволяет оценивать (качественно) социально -
экономико - экологическое состояние некоторой среды по задаваемым
пользователям (экспертом) количественным оценкам тех или иных
параметров среды (выбираемых из базы знаний системы). Для каждого
входного фактора в диалоговом режиме задаются относительные (от 0 до 1)
оценки влияния этого фактора (вес фактора). После анализа этих данных
(этой экологической обстановки) система принимает на основе базы знаний
решение о состоянии социально-экологической среды, используя удельную
количественную оценку (от 0 до 1) и десятибалльную качественную систему
оценок. Функции и работу системы характеризует нижеприведённый
сценарий и протокол диалога с этой системой.
Рассматривается база знаний и экспертная система “Социально-
экономико - экологическая система”, которая построена (Казиевым В. М. и
студентом КБГУ Тебуевым М. Д.) с использованием аппарата нечётких
множеств и логики и позволяет оценивать (качественно) социально -
экономико - экологическое состояние некоторой среды по задаваемым
пользователям (экспертом) количественным оценкам тех или иных
параметров среды (выбираемых из базы знаний системы). Для каждого
входного фактора в диалоговом режиме задаются относительные (от 0 до 1)
оценки влияния этого фактора (вес фактора). После анализа этих данных
(этой экологической обстановки) система принимает на основе базы знаний
решение о состоянии социально-экологической среды, используя удельную
количественную оценку (от 0 до 1) и десятибалльную качественную систему
оценок. Функции и работу системы характеризует нижеприведённый
сценарий и протокол диалога с этой системой.
Экспертная система
(23.02.1998 - Понедельник, 11: 23: 37)
Входные данные:
- Контроль над эрозией: 0.6
- Сооружения для отдыха: 0.1
- Ирригация: 0.9
- Сжигание отходов: 1.0
- Строительство мостов и дорог: 0.6
- Искусственные каналы: 0.5
- Плотины: 0.3
- Туннели и подземные сооружения: 0.9
- Взрывные и буровые работы: 0.45667
- Открытая разработка: 0.567
- Вырубка лесов: 0.345
- Охота и рыболовство: 0.234
- Растениеводство: 0.678
- Скотоводство: 0.648
- Химическая промышленность: 0.2456
- Лесопосадки: 0.54846
- Удобрения: 0.6
- Регулирование диких животных: IGNORE (игнорирование фактора)
- Автомобильное движение: 0.6
- Трубопроводы: 0.0
- Хранилища отходов: 0.0
- Использование ядохимикатов: 0.2
- Течи и разливы: 0.0
Принятие решения о социально-экономико-экологической обстановке:
- Состояние почвы: 0.55177 (слабое положительное)
- Состояние поверхностных вод: 0.52969 (слабое положительное)
- Качественный состав вод: 0.62299 (некоторое положительное)
- Качественный состав воздуха: 0.61298 (некоторое положительное)
- Температура воздуха: 0.48449 (слабое отрицательное)
- Эрозия: 0.59051 (слабое положительное)
- Деревья и кустарники: 0.54160 (слабое положительное)
- Травы: 0.59051 (слабое положительное)
- Сельхозкультуры: 0.51698 (слабое положительное)
- Микрофлора: 0.48702 (слабое отрицательное)
- Животные суши: 0.59804 (слабое положительное)
- Рыбы и моллюски: 0.51525 (слабое положительное)
- Насекомые: 0.56000 (слабое положительное)
- Заболачивание территории: 0.50000 (слабое положительное)
- Курорты на суше: 0.52729 (слабое положительное)
- Парки и заповедники: 0.54668 (слабое положительное)
- Здоровье и безопасность: 0.62870 (некоторое положительное)
- Занятость людей: 0.51196 (слабое положительное)
- Плотность населения: 0.55539 (слабое положительное)
- Соленость воды: 0.48750 (слабое отрицательное)
- Солончаки: 0.57000 (слабое положительное)
- Заросли: 0.62935 (некоторое положительное)
- Оползни: 0.70588 (выраженное положительное)
Пакеты прикладных программ (ППП).
 ППП - комплекс программ,
имеющих следующие особенности (отличающие его от "большого
программного комплекса"):
ППП - комплекс программ,
имеющих следующие особенности (отличающие его от "большого
программного комплекса"):
- наличие управляющей всеми программами ППП программы (монитора);
- наличие языка запросов (оформления и расшифровки заданий для ППП);
- ориентация ППП на достаточно широкий класс однотипных задач;
- расширяемость, модифицируем ость функций (программ) ППП;
- наличие средств для работы с базами данных, операционными системами.
 Пример интегрированного ППП - простой и универсальный пакет
статистического анализа данных SPSS. Интерфейс пользователя с SPSS для
Windows реализуется с помощью простых меню и диалоговых окон т.е. как и
предыдущая разработка, SPSS свободна от использования специально
изучаемого командного языка пакета. Имеется редактор Data Editor для
визуального контроля вводимых данных, функционально аналогичный,
например, Excel. По столбцам отображаются варьируемые переменные, а по
строкам - наборы их вариации, причем с каждой из переменных можно
ознакомиться, вызвав её имя. Ввод данных - аналогичен вводу данных,
например, в Excel. В диалоговых окнах можно определять и сложных
выражений арифметического или логического типа, используемых далее в
расчётах.
Пример интегрированного ППП - простой и универсальный пакет
статистического анализа данных SPSS. Интерфейс пользователя с SPSS для
Windows реализуется с помощью простых меню и диалоговых окон т.е. как и
предыдущая разработка, SPSS свободна от использования специально
изучаемого командного языка пакета. Имеется редактор Data Editor для
визуального контроля вводимых данных, функционально аналогичный,
например, Excel. По столбцам отображаются варьируемые переменные, а по
строкам - наборы их вариации, причем с каждой из переменных можно
ознакомиться, вызвав её имя. Ввод данных - аналогичен вводу данных,
например, в Excel. В диалоговых окнах можно определять и сложных
выражений арифметического или логического типа, используемых далее в
расчётах.
 Опишем расчёты с использованием ППП по анализу систем и динамики
задолженности, например, множественный регрессионный анализ; результаты
одного такого анализа с помощью авторского ППП приведены ниже.
Опишем расчёты с использованием ППП по анализу систем и динамики
задолженности, например, множественный регрессионный анализ; результаты
одного такого анализа с помощью авторского ППП приведены ниже.
 Смысл переменных: х(1) - коэффициент
абсолютной ликвидности; х(2) - коэффициент текущей ликвидности;
х(3) - дебиторская задолженность; х(4) - кредиторская задолженность;
х(5) - превышение кредиторской задолженности
над дебиторской; х(6) - коэффициент финансовой зависимости; х(7) -
коэффициент соотношения привлечённых и собственных средств; х(8) -
кредиторская задолженность перед бюджетом; х(9) - кредиторская
задолженность по социальному страхованию и внебюджетным платежам; х(10)
- коэффициент собираемости налоговых платежей; х(11) - коэффициент
собираемости налога на добавленную стоимость.
Смысл переменных: х(1) - коэффициент
абсолютной ликвидности; х(2) - коэффициент текущей ликвидности;
х(3) - дебиторская задолженность; х(4) - кредиторская задолженность;
х(5) - превышение кредиторской задолженности
над дебиторской; х(6) - коэффициент финансовой зависимости; х(7) -
коэффициент соотношения привлечённых и собственных средств; х(8) -
кредиторская задолженность перед бюджетом; х(9) - кредиторская
задолженность по социальному страхованию и внебюджетным платежам; х(10)
- коэффициент собираемости налоговых платежей; х(11) - коэффициент
собираемости налога на добавленную стоимость.
 Были проведены различные вычислительные эксперименты, например,
если: х(1) - коэффициент абсолютной ликвидности, х(2) - текущей
ликвидности, х(6) - финансовой зависимости, х(7) - коэффициент
привлечения собственных средств, а y = х(10) - коэффициент собираемости
налогов, то находится зависимость коэффициента собираемости налогов от
коэффициентов абсолютной ликвидности, текущей ликвидности, финансовой
зависимости и привлечения собственных средств, т.е. зависимость вида
Были проведены различные вычислительные эксперименты, например,
если: х(1) - коэффициент абсолютной ликвидности, х(2) - текущей
ликвидности, х(6) - финансовой зависимости, х(7) - коэффициент
привлечения собственных средств, а y = х(10) - коэффициент собираемости
налогов, то находится зависимость коэффициента собираемости налогов от
коэффициентов абсолютной ликвидности, текущей ликвидности, финансовой
зависимости и привлечения собственных средств, т.е. зависимость вида
 Типы экспериментов определяются экономическими соображениями,
например, с целью выявления факторов, наиболее влияющих на собираемость
налогов (на коэффициент собираемости налогов).
Типы экспериментов определяются экономическими соображениями,
например, с целью выявления факторов, наиболее влияющих на собираемость
налогов (на коэффициент собираемости налогов).
БАКСАНСКИЙ РАЙОН КБР
(205 предприятия(й))
 Регрессионная модель вида
Y = a(0) + a(1)*x(1) + ... + a(7)*x(7)
Регрессионная модель вида
Y = a(0) + a(1)*x(1) + ... + a(7)*x(7)
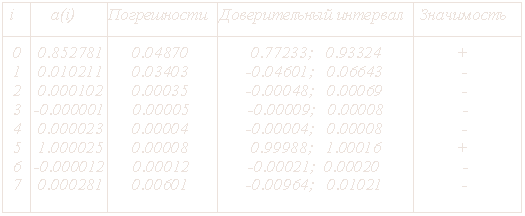
Таблица 1.
Таблица коэффициентов модели
Примечание: "+" - коэффициент значим, "-" - коэффициент не значим.
Коэффициент множественной корреляции значим и равен: 0.98.
Таблица 2.
Таблица корреляции y и x(i), i=1,2,...,7
Таблица 3.
Таблица адекватности модели
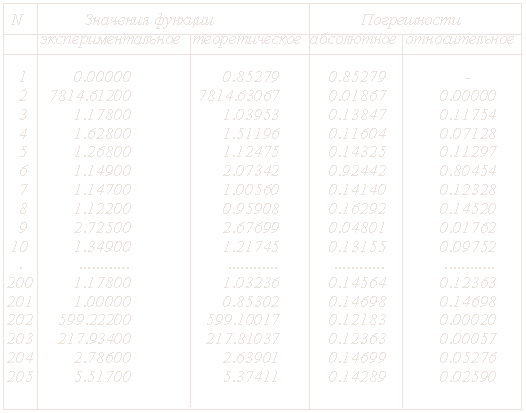 Рис. 27. Фрагменты результатов вычислительных экспериментов.
Рис. 27. Фрагменты результатов вычислительных экспериментов. В результате анализа проведенных экспериментов по каждому району,
городу найдена регрессионная зависимость с очень высокой степенью
адекватности; коэффициент множественной корреляции равен 0.99 - 1.0, а
относительная погрешность в среднем порядка 5 - 8 процентов (для таких
зависимостей такая погрешность считается очень низкой).
В результате анализа проведенных экспериментов по каждому району,
городу найдена регрессионная зависимость с очень высокой степенью
адекватности; коэффициент множественной корреляции равен 0.99 - 1.0, а
относительная погрешность в среднем порядка 5 - 8 процентов (для таких
зависимостей такая погрешность считается очень низкой).
При этом:
- использованная программа работает качественно, например, имевшиеся в
исходных данных сильные колебания параметров (колебания от 7814.612 до
0) моделью "ухвачены" и отражены;
- вычисленные доверительные интервалы коэффициентов зависимостей
можно использовать для определения наилучших и наихудших прогнозных
значений функции отклика;
- погрешности коэффициентов можно использовать для коррекции влияния
тех или иных параметров в рамках рассматриваемой модели (найденной
зависимости), а полученные зависимости можно использовать для
краткосрочного прогноза.
Вопросы для самоконтроля
- Какая модель называется статической (динамической, дискретной,
непрерывной, имитационной, детерминированной)? Приведите пример
каждой модели.
- Перечислите три задачи моделирования и примеры по каждой задаче
из различных областей.
- Перечислите свойства моделей. Как эти свойства взаимосвязаны?
Приведите примеры, убедительно показывающие необходимость каждого из
этих свойств.
- Перечислите основные этапы жизненного цикла моделирования.
- Что такое оценка адекватности модели? Оцените адекватность какой-
либо модели.
- Что такое вычислительный или компьютерный эксперимент?
- Перечислите основные направления применения моделей и приведите
примеры по каждому из них.
- В чем особенности компьютерного моделирования по сравнению с
математическим моделированием?
- Перечислите этапы (задачи этапов) компьютерного моделирования.
- Приведите примеры актуальности использования новых технологий.
- Приведите различные примеры использования новой
информационной технологии в различных областях знания, в познании.
- Приведите примеры, показывающие роль новых информационных
технологий в развитии общества, в социальной сфере, в развитии
инфраструктуры общества.