5.1. Нечеткие цели, ограничения и решения
Возникновение иерархической структуры управления было обусловлено все возрастающей сложностью технологии управляемых объектов, создающей большие трудности для централизованного управления. Поэтому появилась необходимость разделения всего процесса принятия решений на такое число уровней, чтобы решение задачи оптимизации на каждом из них было не сложным. Но с возникновением многоуровневых иерархических систем управления появилась и новая задача согласования и координации решений, принимаемых на всех уровнях управления.
Общая схема координации в двухуровневой системе сводится к следующему. Элементы передают в центр набор вариантов своей работы. Каждый вариант представляет собой векторный показатель элемента, допустимый с точки зрения его локальных ограничений. На основании получаемых от элементов вариантов центр формирует план, оптимальный с точки зрения всей системы [9]. Этот план передается элементам и, далее, детализируется ими.
Однако при моделировании сложных систем невозможно учесть достаточно большое число реальных факторов, поскольку это привело бы к чрезмерному усложнению модели. Поэтому в модель приходится вводить лишь ограниченное число таких факторов, которые по тем или иным соображениям считаются наиболее существенными. При этом возможны два подхода. Неучтенные в описании модели факторы можно считать абсолютно несущественными и полностью их игнорировать при принятии решений с использованием этой модели. С другой стороны, при втором подходе можно явно не вводить "несущественные факторы" в математическую модель, но учитывать их влияние, допустив, что отклик модели на то или иное воздействие (выбор альтернативы) может быть известным лишь приближенно или нечетко.
В традиционном подходе главными элементами процесса принятия решения являются:
1. множество альтернатив,
2. множество ограничений, которые необходимо учитывать при выборе между различными альтернативами,
3. функция предпочтительности, определяющая переход из пространства альтернатив в некоторое другое пространство и ставящая каждой альтернативе в соответствие выигрыш (или проигрыш), который получают в результате выбора этой альтернативы.
При рассмотрении этого процесса с более общих позиций принятия решений в нечетких условиях естественной представляется другая логическая схема, отличительной чертой которой является симметрия по отношению к целям и ограничениям [54]. Эта симметрия устраняет различия между целями и ограничениями и позволяет достаточно просто сформировать на их основе решение.
Под нечеткой целью подразумевается цель, которую можно описать как нечеткое множество в соответствующем пространстве. Пусть Х - заданное множество альтернатив. Тогда нечеткая цель, или просто цель, G будет определяться фиксированным нечетким множеством G в Х [98].
При обычном
подходе функция
предпочтительности, используемая в
процессе принятия решения, служит
для установления линейной
упорядоченности на множестве
альтернатив. Очевидно, что функция
принадлежности ![]() нечеткой цели
выполняет ту же задачу и может быть
получена из функции
предпочтительности с помощью
нормализации, сохраняющей
установленную линейную
упорядоченность.
нечеткой цели
выполняет ту же задачу и может быть
получена из функции
предпочтительности с помощью
нормализации, сохраняющей
установленную линейную
упорядоченность.
Подобным же образом нечеткое ограничение, или просто ограничение, С в пространстве Х определяется как некоторое нечеткое множество в Х. Важным моментом здесь является то, что и цель и ограничение рассматриваются как нечеткие множества в пространстве альтернатив; это дает возможность не делать между ними различия при формировании решения.
Решение - это по существу выбор одной или нескольких из имеющихся альтернатив. Проблема принятия решения в нечетких условиях интерпретируется тогда как комплексное влияние нечеткой цели G и нечеткого ограничения С на выбор альтернатив и характеризуется пересечением G C C, которое и образует нечеткое множество решений D, т.е.
D = G C C.
Функция принадлежности для множества решений задается соотношением
![]() .
.
В более общем случае, если имеется n целей и m ограничений, то результирующее решение определяется пересечением всех заданных целей и ограничений, т.е.
![]()
и, соответственно,
![]() .
.
В приведенном определении нечеткие цели и ограничения входят в выражение для D совершенно одинаковым образом. Такое определение решения как нечеткого множества в пространстве альтернатив может показаться несколько искусственным. На самом деле оно совершенно естественно, поскольку нечеткое решение может рассматриваться как некоторая "инструкция", нечеткость которой является следствием неточности формулировки поставленных целей и ограничений.
Во многих случаях все же разумно выбирать те альтернативы, которые имеют максимальную степень принадлежности к D. Если таких элементов несколько, то они образуют обычное множество, которое называется оптимальным решением, а каждый элемент этого множества - максимизирующимрешением.
Практический интерес представляет более общий случай, когда цели и ограничения - нечеткие множества в разных пространствах. Пусть f - отображение из Х в Y, причем переменная х обозначает входное воздействие, а у - соответствующий выход.
Предположим, что
цель задана как нечеткое множество G в Y, в то время как
ограничение - нечеткое множество Св
пространстве Х. Имея нечеткое
множество GвY
, можно найти
нечеткое множество`Gв Х, которое
индуцирует Gв
Y. Функция
принадлежности ![]() в Y задается равенством
в Y задается равенством
![]() .
.
После этого
решение D может
быть выражено пересечением
множеств ![]() и С. Используя
предыдущее соотношение, можно
записать
и С. Используя
предыдущее соотношение, можно
записать
![]() .
.
Таким образом, случай, когда цели и ограничения задаются как нечеткие множества в разных пространствах, может быть сведен к случаю, когда они задаются в одном и том же пространстве.
5.2. Основные принципы управления многоуровневыми иерархическими системами
В настоящее время вопросам принятия решений в сложных иерархических системах уделяется большое внимание как в нашей стране, так и за рубежом [68, 123, 155, 182, 264, 269, 271, 293, 299, 303, 316, 337, 344, 352].
К достоинствам иерархической структуры автоматизированного управления, в которой на нижнем уровне имеется большое количество несложных задач, а на вышестоящих уровнях - небольшое число сложных задач, следует отнести (согласно зарубежным данным) снижение общей стоимости обработки информации в системе, повышение пропускной способности хост-машины в сети ЭВМ и устойчивость к отказам. Критические для системы функции продолжают выполняться локальными системами управления при выходе из строя хост-машины или линий связи.
Теоретические вопросы построения систем многосвязной стабилизации параметров в замкнутых локальных контурах регулирования, полученных в результате декомпозиции исходной задачи оптимизации рассматриваются в работах [264, 269, 299]. Рассматриваемые системы имеют смешанную замкнуто-разомкнутую структуру и сочетают управления по отклонению и по возмущению. При этом динамическая стабилизация параметров производится в основном замкнутым локальным контуром, а коррекция по низкочастотным (НЧ) возмущениям осуществляется системой верхнего уровня.
Разделение решения общей оптимизационной задачи между двумя взаимосвязанными уровнями может чаще всего производиться на основе гипотезы малости влияния режимных величин на условия материального баланса, позволяющей воспользоваться формальными схемами теории возмущений [74] (малость нелинейных слагаемых в моделях).
Общая задача оптимального управления иерархическими системами обычно ставится как статическая оптимизационная задача, т.к. рассматривается задача функционирования производства на достаточно больших интервалов времени (сутки и более), во время которых динамикой протекания процессов можно пренебречь [74].
Высокочастотные возмущения материальных потоков, как предполагается в этом случае, отрабатываются системами автоматической стабилизации работы отдельных установок и диспетчерскими службами нижнего уровня. Решение общей задачи управления всем технологическим комплексом в целом на ЭВМ в реальном масштабе времени для нахождения режимов работы всех установок , входящих в производство, невозможно из-за нелинейности моделей и огромной размерности задачи (до десятков тысяч переменных) [74]. Решение отдельных локальных задач оптимизации для ряда подсистем и элементов без решения общей задачи оказывается, чаще всего мало или совершенно неэффективным, т.к. не определены переменные, согласующие режимы работ подсистем между собой, и не скоординированы критерии эффективности.
Существует два вида алгоритмов координации: итеративные и безытеративные [9]. В существующих в настоящее время итеративных процедурах (алгоритмы Данцига-Вульфа, алгоритм Корнаи-Липтака, методы, основанные на введение функции Лагранжа или ее различных модификаций, алгоритмы оптимизации сложных химико-технологических схем Балакирева В.С., Володина В.М., Цирлина А.М., обобщающая схема итеративных алгоритмов Алиева Р.А., Либерзона М.И.) оптимальное решение определяется в ходе итеративного обмена информацией между центром и элементами, а на каждом шаге итеративного процесса решаются локально-оптимальные задачи элементов и координирующая задача центра.
При внедрении итеративных процедур согласования решений в многоуровневых иерархических системах возникают непреодолимые преграды из-за больших межуровневых информационных потоков и, соответственно, больших затрат времени на обмен информацией [10, 74]. Альтернативой этому подходу служит использование в вышестоящих подсистемах детальных моделей нижестоящих подсистем, однако при этом не используются преимущества децентрализованного управления. В безытеративных алгоритмах принятие решения осуществляется в результате однократного обмена информацией между уровнями. В этом случае координирующая подсистема может иметь для детерминированного варианта детальные модели подсистем и точно знать их целевые функции, однако такой подход приводит к потере преимуществ децентрализованного управления и очень сложной задаче для вышестоящего уровня. В основном безытерационные алгоритмы сводятся к построению множества эффективных решений [9]. Для организационных иерархических систем в работах [9, 10] приведены алгоритмы координации, основанные на нечеткой логике и композиционном правиле Заде. В работах [11, 134] была предложена безытеративная процедура принятия решений в многоуровневой иерархической системе на основе теории нечетких множеств и нечеткого динамического программирования Беллмана-Заде, а также численный матричный метод для случая выпуклых функций принадлежности для подсистем. Соответственно недостатком всех безытеративных алгоритмов является необходимость определения и передачи на вышестоящий уровень управления всего эффективного множества элементов (или достаточно точной аппроксимации этого множества) [9]. Однако алгоритмы, основанные на теории нечетких множеств, позволяют строить эффективные множества только для координирующих параметров в интервалах заданного r-уровня с учетом фактической неопределенности для объекта управления.
В [344] предлагается метод, основанный на декомпозиции общей задачи управления на подзадачи. Этот метод позволяет явно сформулировать все допущения, которые принимаются при замене общей задачи на подзадачи. Однако при применении этого метода могут возникнуть трудности получения структуры подзадач и принципов координации, совместимых с реально существующими методами управления технологическими процессами.
Для многоуровневой организационно-технологической системы (типа ГПУ Тюменьгазпрома) межуровневая и внутриуровневая координация отличается уровнем организации взаимодействия [155, 305] :
1. Координация по целям. Система управления вышестоящего уровня может устанавливать для нижестоящей подсистемы цели функционирования и характеризующие их показатели с заданием их количественных значений на планируемый период, т.е. целевая функция подсистемы формируется вышестоящим уровнем.
2. Координация по ограничениям. В этом случае на ряд параметров в точках сопряжения подсистем устанавливаются ограничения вышестоящей системой управления. Эти ограничения задаются с системных позиций и учитывают цели и ограничения подсистем.
3. Координация во времени (синхронизация работы подсистем).
4. Координация по входным или выходным параметрам.
5. Координация по целям [271].
Можно выделить также различные виды координирующих воздействий:
1. Интегральная координация (слабая), когда для каждой подсистемы задается плановый показатель К на определенный период времени Т и различные ограничения (нормативы) (потери газа, потребление газа на собственные нужды и т.д.):
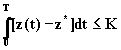 . (5.1)
. (5.1)
2. Четкая координация (жесткая), когда для координируемого параметра К в каждый момент времени выставляется требование соблюдения равенства К(t) = К.
3. Интервальная координация, которая требует лишь принадлежности координирующего параметра К заданному интервалу
![]() .
.
4. Лингвистическая
координация, при которой
осуществляется выдача нечетких
координирующих воздействий на
естественном языке, например:
"Давление в узле А должно быть
около 7 МПа". В этом случае
координирующая величина К является
нечеткой и задается функцией
принадлежности ![]() . Важным вопросом
является и выбор принципа
координации [155, 305]: прогнозируемого
взаимодействия, сбалансированного
взаимодействия, оцененного
взаимодействия, координирующий
принцип нагрузочного типа и
координирующий принцип
коалиционного типа.
. Важным вопросом
является и выбор принципа
координации [155, 305]: прогнозируемого
взаимодействия, сбалансированного
взаимодействия, оцененного
взаимодействия, координирующий
принцип нагрузочного типа и
координирующий принцип
коалиционного типа.
Центральной проблемой разработки распределенных процедур решения сложных задач является нахождение такой декомпозиции задачи на подзадачи и выбор таких методов их решения, которые приводили бы к получению приемлемого по качеству решению всей задачи в целом за приемлемое время [187]. Формальные методы такой декомпозиции в настоящее время разработаны крайне слабо [187] и в основном для хорошо формализованных задач определенного класса (задача линейного программирования большой размерности [176]).
Существующие методы декомпозиции в основном сводятся к последовательной замене системы нелинейных дифференциальных уравнений в частных производных системой нелинейных алгебраических уравнений, а затем после линеаризации - к системе линейных уравнений [292].
Недостатком этого подхода являются экспоненциальный рост машинного времени на расчет с ростом числа элементов системы и использование единого для всех элементов шага квантования времени [317], хотя элементы могут характеризоваться временными квантами, отличающимися друг от друга на порядок и более. Та же самая проблема возникает и при решении задачи квантования по пространственным координатам. Выходом из такого положения может стать разработка специальных декомпозиционных процедур, допускающих наличие у подсистем разного уровня разных квантов по параметрам и времени.
В этом случае модель процесса управления автоматизированным технологическим комплексом становится адекватной существующей на практике политике управления. Возникающая вследствии декомпозиции сложной задачи управления параллельность решения ряда задач делает этот подход пригодным для реализации общей задачи управления на многомашинном многоуровневом вычислительном комплексе [317].
В основе декомпозиционного подхода лежит предположение о наличии общей, глобальной модели, которая описывает основные свойства системы адекватно поставленным целям принятия решения (или исследования). При наличии такой модели применение декомпозиционых методов позволяет резко сократить размерность решаемой задачи и свести ее к последовательному решению ряда задач намного меньшей размерности. Все модели, ограничения и критерии этих задач непосредственно вытекают только из специальным образом расчлененной глобальной целевой функции. При декомпозиционном подходе алгоритм взаимодействия между подсистемами (решаемыми задачами) и характер потоков информации между вышестоящими и нижестоящими уровнями являются производными и определяются методом декомпозиции глобальной задачи.
Основные положения теории многоуровневых иерархических систем были разработаны в монографии [155]. В этой работе предложены некоторые принципы декомпозиции системной целевой функции и ограничений на целевые функции и ограничения, соответствующие отдельным подсистемам.
Каждая подсистема оптимизирует свою целевую функцию, а верхний уровень координирует решения нижестоящих подсистем таким образом, чтобы достигался оптимум глобальной целевой функции. Процесс координации осуществляется с помощью некоторых фиктивных переменных, которые для нижестоящих подсистем являются параметрами.
Используя результаты работы [155], можно получить конструктивные решения лишь для простейших линейных систем, так как обсуждаемые авторами проблемы формулируются на высоком уровне математической абстракции. Но вместе с тем эта работа дает понятийный аппарат для рассмотрения иерархических систем и создает возможность построения количественной теории для многоуровневых систем.
Задачи, критерии и фиктивные переменные подсистем различных уровней при декомпозиции могут не соответствовать реальным функциям управляющих органов и диспетчерских служб этих подсистем. Поэтому применить процесс декомпозиции в чистом виде для реальной системы представляется затруднительным.
Анализ и синтез иерархических систем непосредственно не сводится к классической теории оптимальных систем, которая имеет дело только с одноуровневыми и одноцелевыми системами [162]. Иерархические системы относятся к классу многоуровневых и многоцелевых систем. В этих системах изменяется само понятие оптимальности, поэтому очень важно найти адекватные математические постановки задач и вложить разумный смысл в понятие оптимальности.
Ю.И. Павловским исследована возможность строгого подхода к агрегированию и построению иерархических управляющих структур для сложных систем. Рассматривая вопрос об определении числа уровней в проектируемых системах, он отмечает, что формальная постановка задачи о выборе иерархической системы управления в терминах только описания процесса затруднительна [182].
В [246] предлагалось при декомпозиции применять теорию графов, на основе которой можно ввести различные операции преобразования графа: исключение ребер, эквивалентирование, стягивание и декомпозиция элементов графа. Декомпозиция на подзадачи осуществляется за счет предварительной формулировки требований к режиму системы и различных условий и затем к получению новой совокупности задач за счет пренебрежения некоторыми условиями и предположениями.
В работе [161] приведен алгоритм согласования решений в распределенной системе взаимосвязанных задач с линейными моделями для двухуровневой иерархической системы. Новый алгоритм многоуровневого управления для сложных систем приведен в [257]. Здесь рассмотрена задача построения многоуровневого регулятора для сложной системы путем построения локальных регуляторов для каждой из подсистем, входящих в исходную систему, и последующего решения соответствующей задачи для всего регулятора в целом для систем со статическими взаимосвязями.
Некоторые вопросы управления многостадийными и многофазными технологическими процессами при последовательном (каскадном) соединении отдельных стадий обсуждаются в [342].
Применение блочно-импульсного преобразования к иерархическому управлению линейными нестационарными системами описывается в работе [346].
Методы статистической и динамической оптимизации иерархических систем, особенно их идентификации и условия робастности приведены в работе [316].
Вопросам создания алгоритмов формализованного распределения задач в иерархических системах по элементам и уровням системы управления посвящена работа [132].
Преимущества использования иерархической структуры управления для сложных нелинейных объектов с экспериментальной проверкой показаны в работе [299].
Важным фактором является учет многокритериальности задачи управления сложным многоуровневым технологическим комплексом. Правильное формализованное представление целей системы в значительной мере определяет практическую ценность получаемых решений.
В простейшем
детерминированном случае под
критерием понимается функционал ![]() ,
определенный на множестве
возможных решений, и при
оптимизации необходимо найти
решение
,
определенный на множестве
возможных решений, и при
оптимизации необходимо найти
решение ![]() , обеспечивающее максимум
этого функционала.
, обеспечивающее максимум
этого функционала.
При решении многокритериальной задачи отыскивается решение, обеспечивающее максимум каждого из частных критериев. Однако, такой максимум достигается лишь в идеальном случае, а в реальных задачах требуется компромиссное решение. Поэтому становится необходимым указание последовательности применения критериев и относительной важности частных критериев.
Классические методы оптимизации (принцип максимума Понтрягина, метод динамического программирования Беллмана) позволяют решать задачи только со скалярным критерием [229]. При наличии векторного критерия применение этих методов оптимизации возможно только путем синтеза (чаще всего аддитивного) одного обобщенного критерия из частных критериев или введением всех (кроме основного) критериев в качестве дополнительных ограничений или штрафных функций.
Необходимость перевода векторного критерия в скалярный критерий оптимизации привела к введению специальных функций предпочтения решений, т.е. акцент все больше переносится на проблему предварительного определения преимущества того или иного решения [162].
Наиболее часто при решении многокритериальных задач применяются синтетические показатели качества - аддитивные, мультипликативные и минимаксные критерии.
Аддитивный глобальный критерий качества определяется следующим образом :
![]() , (5.2)
, (5.2)
где N - число частных критериев эффективности, причем в частном случае могут использоваться и дополнительные условия нормировки
![]() и
и ![]() . (5.3)
. (5.3)
Весовые коэффициенты для частных критериев подбираются субъективно, на основе экспертных оценок, однако имеются и методы объективного определения весов (например, из решения статистической игры с критерием минимизации экономических потерь при принятии решений [80]).
Основным недостатком аддитивного критерия является возможность компенсации одного критерия за счет других.
Мультипликативный глобальный критерий имеет вид
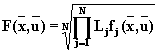 (5.4)
(5.4)
а минимаксный
![]() . (5.5)
. (5.5)
Мультипликативный критерий не допускает компенсации, и если значение одного из частных критериев равно нулю, то глобальный критерий также равен нулю. К достоинствам минимаксного критерия можно отнести тот факт, что для него не происходит смещения оптимума при добавлении новых несущественных критериев, но в тоже время он ухудшает чувствительность глобального критерия.
При возможности ранжирования критериев по важности для нахождения численного решения нередко применяется метод последовательных уступок.
Если в системе
имеется неопределенность, то
задача принятия решения
значительно усложняется. В случае
статистической неопределенности
(при известных распределениях
случайных параметров) при наличии
векторной целевой функции решение
обычно характеризуется не одним, а
несколькими числами и роль целевых
функций ![]() играют определенные
параметры распределения, причем
наиболее известными примерами
являются математическое ожидание М
и дисперсия D,
моменты высших порядков
применяются редко.
играют определенные
параметры распределения, причем
наиболее известными примерами
являются математическое ожидание М
и дисперсия D,
моменты высших порядков
применяются редко.
Иногда применяются и обычные функционалы, определенные на множестве решений, однако эти критерии уже носят вероятностный характер: они означают вероятности появления некоторых событий (например, вероятность безотказной работы оборудования и т.д.).
В работе [9] проводится анализ и обобщение существующих алгоритмов координации на основании следующих введенных понятий:
1. множество эффективных точек Р* или множества Парето (обладающих тем свойством, что невозможно улучшить значение какого-либо частного критерия для подсистемы по сравнению со значением, достигаемым этим критерием в точке х, без ухудшения значения хотя бы одного из прочих частных критериев);
2. множество
полуэффективных точек R* (если ![]() , то не существует
допустимой альтернативы,
улучшающей значение сразу всех
частных критериев);
, то не существует
допустимой альтернативы,
улучшающей значение сразу всех
частных критериев);
3. множество
допустимых значений ![]()
критериев.
Одним из существенных достоинств решения многокритериальной задачи является тот факт, что в результате решения однокритериальной задачи мы получаем решение на границе какого-либо ограничения, т.е. она по сути представляет собой "генератор" узких мест, которые "болезненно" отражаются на поведении реального объекта и значительно снижают другие показатели режима работы системы - надежность, оптимальность и т.д. Многокритериальная постановка задачи отличается большей близостью к реальной задаче и меньшей долей абстракции [130].
Для реальных систем характерна зависимость выбора критерия (или группы критериев) оптимизация от окружающей среды и ряда других факторов; т.е. в зависимости от ситуации должен проводиться выбор вектора критериев (или одного критерия) в процессе принятия решения оптимальным образом, а не вводиться в систему жестко или волевым путем. Особо важное значение приобретают вопросы анализа зоны применимости различных критериев и выявления возможности решения однокритериальных задач в частном случае. Поэтому становится возможным объективно провести выбор критериев по степени их применимости. Одним из существенных достоинств метода оптимизации можно считать тот факт, что изменение критерия оптимизаций и переход к векторной оптимизации, изменение ограничений не приводит к переходу к совершенно новой задаче и даже к смене метода решения задачи, т.е. метод оптимизации должен обладать достаточной гибкостью.
В настоящее время принят такой подход к постановкам задачи, что критерии принятия решений не входят в модель и задаются человеком до начала решения задачи на ЭВМ. Однако субъективизм выбора критерия крайне велик в этом случае. Выбор того или иного критерия полностью определяется состоянием системы и внешней среды, а также степенью неопределенности по различным показателям, параметрам и характеристикам системы. Рассматривая концептуальные уровни описания сложной иерархической плохо определенной системы согласно [259] можно выделить три уровня описания с характерной для каждого из них степенью абстрагирования и детализации:
1. Методологический уровень. Использование на этом уровне теории сжатых множеств позволяет адекватно отобразить задачу управления сложным многоуровневым иерархическим комплексом, провести декомпозицию этой задачи на ряд более простых иерархических взаимодействующих задач с использованием основных операций сжатых множеств [49].
2. Алгоритмический уровень. С учетом имеющейся в системе неопределенности могут быть использованы детерминированные методы, теории нечетких, интервальных или случайных множеств. В данной работе основное внимание уделяется алгоритмам принятия решения на базе теории нечетких множеств [98] и интервального анализа [247]. Применение теории нечетких множеств позволяет построить конструктивные алгоритмы для расчета, идентификации и оптимизации для каждой из полученных с помощью сжатых множеств задач.
3. Операциональный уровень. Для расчета и оптимизации на основе полученных на втором уровне алгоритмов необходимо иметь аналитические и численные методы оперирования с нечетким и интервальными величинами, методы решения задач нечеткого и интервального линейного и нелинейного программирования, получения решений систем обычных и дифференциальных уравнений. Имеются также различные способы сведения задач нечеткого математического программирования к совокупности задач интервального программирования, а также к обычным детерминированным задачам, что дает возможность воспользоваться хорошо разработанными методами и пакетами программ математического программирования [166]. Требуются также конструктивные методы построения функций принадлежности.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]