7.5. Алгоритм расчета запасов газа объемным методом по неточным промысловым данным

Совершенствование методов подсчета запасов газа и рациональных методов разведки месторождений природных газов является весьма актуальным вопросом на современном этапе развития газодобывающей промышленности. Необходимость совершенствования этих методов обусловливается задачей скорейшего ввода в разработку месторождений природных газов на основе достоверного подсчета запасов газа в минимальные сроки и при минимальных капиталовложениях.

Расчетные методы и соответствующие исследования скважин и пластов должны позволять определять параметры газоносных и водоносных пластов и их изменение по мощности и по площади. Без достоверного знания параметров пластов невозможно строить правильный прогноз разработки месторождений, регулировать процесс разработки, находить оптимальные проектные решения и т. д. От точности решения этой задачи в значительной степени зависят стратегия извлечения запасов газа и эффективность использования капитальных вложений на обустройство и доразбуривание месторождений.

Неопределенность имеет место в основном из-за нечеткости понятий "пористость", "мощность" и т.д. для месторождения в целом. Имеются лишь замеры этих параметров в отдельных точках месторождений, а ввиду неоднородности среды эти величины значительно меняются в пространстве. Применение средних и средневзвешенных значений параметров для расчетов может приводить к получению значительно смещенных точечных оценок параметров.

В нашей стране оценивание запасов производится в основном с использованием детерминированных методов и результирующая оценка является точечной. Лишь для расчета отдельных параметров в моделях используются статистические методы, различные методы усреднения и взвешивания [85]. В то же время в США, Японии и других зарубежных странах запасы нефти и газа определяются и утверждаются в виде функций распределения вероятности [236]. Однако, особенно на ранних стадиях освоения месторождений, данных для построения функций распределения вероятностей по каждому параметру бывает недостаточно. К тому же операции с этими функциями в теории вероятностей очень громоздки и для решения практических задач чаще всего используется метод Монте-Карло [236].

Ситуация усложняется тем, что существуют различные методы оценки запасов и, ввиду значительной погрешности исходных данных, результаты расчетов являются противоречивыми, хотя наличие избыточности информации должно позволять уточнить оценку запасов. Проведенные исследования показали, что погрешность оценки запасов, которая зависит от точности построения карт изобар, газонасыщенности, пористости, мощности и учета количества добытого газа, достигает 20-30% [85].

Погрешность различных приборов и датчиков, проводимых исследований, наличие по целому ряду параметров возможности лишь косвенной их оценки приводят к необходимости проведения расчетов при наличии неточно заданных параметров и коэффициентов уравнений. Замена неточно заданных величин на детерминированные (точечные ) величины значительно усложняет процедуру расчета, приводит к необходимости их итерационного подбора для получения приемлемых результатов. В этом случае также затруднена оценка погрешности получаемого результата. Очень часто в состав параметров и коэффициентов уравнений входят одновременно величины с различным характером неопределенности: интервальные, нечеткие, стохастические, эвристические (на основе экспертной оценки). Поэтому возникает необходимость представления всей информации на едином формальном языке теории нечетких множеств с представлением характеристик неточно заданных величин в виде F-функций.

Авторами был предложен новый алгоритм оценки запасов в условиях неопределенности геолого-промысловой информации, основанный на теории нечетких множеств [37, 38, 134]. Интерпретация неопределенных величин как нечетких больше соответствует реальной промысловой ситуации по сравнению с интерпретацией этих величин как случайных. Применение для оперирования с неопределенными величинами аппарата теории вероятности приводит к тому, что фактически неопределенность независимо от ее природы отождествляется со случайностью, между тем как основным источником неопределенности во многих процессах принятия решений является нечеткость.

При расчете запасов газа объемным методом воспользуемся известным уравнением [96], однако выделим в нем те величины, которые заданы нечетко:

; (7.11)

где - нечеткий коэффициент газонасыщенности, дол. ед;

- нечеткий коэффициент пористости, дол. ед;

- нечеткая мощность пласта, м;

- нечеткая площадь газоносности, м²;

Z - коэффициент сжимаемости газа;

- пластовое давление, Па;

- пластовая температура, К;

- нечеткие запасы газа, приведенные к нормальным условиям при и , м³.

В отличии от существующей практики предварительного получения точечных оценок для каждого параметра на основе различных способов усреднения, взвешивая по объему и площади в предлагаемом подходе каждый из них задается в виде соответствующей функции принадлежности .

Результирующую функцию принадлежности для запасов газа получаем из уравнения (7.11) с учетом определения алгебраических операций:

(7.12)

Найти по формуле (7.12) аналитическими методами, описанными выше, довольно трудно, поэтому для решения ряда практических задач применяются численные методы. Наиболее простой из них - так называемый обратный метод. В этом случае результирующая функция принадлежности рассчитывается путем последовательного применения бинарной алгебраической операции.

Алгоритм нахождения функции принадлежности как результата алгебраической операции над двумя произвольными функциями принадлежности и обратным численным методом состоит из следующих этапов:

1. Для функций принадлежности , , разобьем отрезок на части точками .

2. Для каждого из решения уравнений , определяем соответствующие -уровневые множества:

;

.

3. Находим -уровневые множества результирующей функции

;

где * - соответствующая интервальная операция.

В качестве примера применения алгоритма приведем расчет запасов газа объемным методом для некоторого гипотетического месторождения. Данные для расчета (табл. 7.2) получают в результате обработки геолого-промысловой информации по этому месторождению с учетом погрешностей замера каждой переменной [85].

По данным таблицы можно построить треугольные функции принадлежности для каждого из параметров:

Таблица 7.2.

Исходные данные для расчета запасов газа

Функции принадлежности могут быть построены более точно с использованием дополнительной информации о методах исследования керна, погрешности соответствующих приборов, данных исследования для всех скважин и т.д. Однако особенности применяемого численного метода позволяют работать с функциями любого вида.

На основе данного алгоритма рассчитаны r-уровневые множества для функции (табл.7.3). В данном случае все функции достигают значения 1, поэтому отрезок [0,1] разбивается на r-уровни (столбец 1 в табл. 7.3).

Результаты второго этапа алгоритма для функций помещены соответственно в столбцы 2, 3, 4, 5. Окончательный результат с учетом умножения на константу С приводится в шестой колонке табл.7.3.

Таблица 7.3.

Рассчитанные r-уровневые множества для функции

График функции , полученный в результате применения обратного численного метода, приведен на рис.7.3 (функция 1).

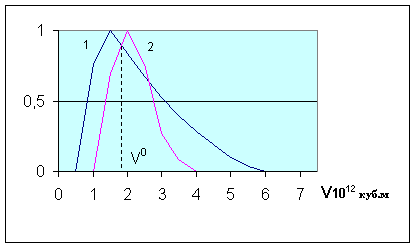
Рис. 7.3. Функции принадлежности для запасов газа

7.6. Оценка запасов газа балансовым методом при наличии неточных замеров

Определение запасов газа по промысловым данным может проводиться и на основе другого балансового метода с учетом динамики падения пластового давления и данных по суммарной добыче газа из месторождения [101]. Разработанные алгоритмы позволяют учесть целый ряд неточно заданных параметров, в том числе процесс обводнения газового месторождения и данные по нечеткой оценке объемов вторгшейся воды. Такая задача подробно рассмотрена авторами в работах [24, 26, 234]. Однако для простоты рассмотрим чисто газовый режим [85]:

(7.13)

где Q_t- суммарная добыча газа к текущему моменту времени t;

P_н, P_t - приведенные средневзвешенные пластовые давления в начальный и текущий моменты времени.

В реальной ситуации точно оценить запасы газа по уравнению (7.13) невозможно ввиду того, что параметр P_tполучается путем взвешивания пластового давления в залежи (что является неточной и неоднозначной процедурой ввиду наличия различных способов взвешивания), а Q _t замеряется со значительной погрешностью.

Для уравнения (7.13) подсчета запасов газа по падению пластового давления нечеткими величинами будем считать суммарную добычу газа с заданной функцией принадлежности объема добытого газа к подмножеству допустимых значений:

и приведенное средневзвешенное пластовое давление с функцией принадлежности:

,

где a, b - определяют точку максимума функций принадлежности, а

c, d - характеризуют степень разброса параметра.

Для определения нечеткой величины запасов газа используем прямой аналитический метод нахождения результатов алгебраических операций. Вначале произведем умножение на константу (-1/P_н ):

.

Тогда для знаменателя (7.13) получаем

.

Для операции деления из уравнения

получаем

,

.

Учитывая объединение результирующих множеств, окончательно имеем

.

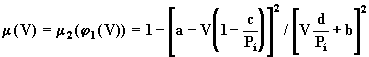В качестве примера оценки запасов по неточным данным построена функция принадлежности для запасов газа а =2? 10¹¹, b=5 ? 10⁹, с=126, d=3,8, P_н=138,5 и приведена на рис.7.3 (функция 2).

7.7. Согласование нечетких решений по запасам газа, полученным по двум различным физическим моделям. Коррекция исходных функций принадлежности для геолого-промысловых параметров

При отсутствии дополнительных предположений о применимости методов (т.е. ) результирующая функция принадлежности для запасов газа будет выглядеть следующим образом:

. (7.14)

Четкое компромиссное решение находится из условия

. (7.15)

При наличии дополнительной информации о применимости методов она может быть учтена при согласовании решений. Например, можно учесть, что достоверность метода подсчета запасов по падению пластового давления возрастает по мере накопления промысловой информации , где Т - текущее время разработки газового месторождения; - время окончания его разработки. Тогда в начальный момент времени наибольший вес имеет нечеткое решение, полученное объемным методом, а с ростом Т нечеткость решения начнет уменьшаться и вес этого метода будет возрастать.

После нахождения системного решения могут быть скорректированы исходные F-функции в формуле (3.25), т.е. уточнены нечеткие параметры . Это можно сделать на основе метода коррекции исходных функций принадлежности [39]. С учетом имеющихся обозначений этой работы , получаем:

.

Тогда по предложенному алгоритму можно уточнить F-функции .

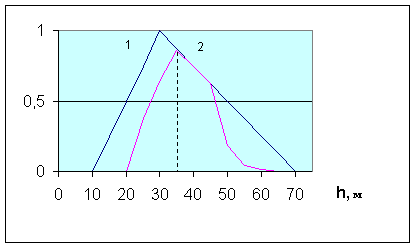
Рис.7.4. Коррекция исходной функции принадлежности для мощности залежи

Таким образом, исходные функции принадлежности для эффективной мощности пласта, площади, пористости, газонасыщенности и т.д. уточняются и в качестве примера на рис.7.4 приведены исходная (1) и откорректированная(2) F-функции для гипотетического месторождения по эффективной мощности пласта.

Важное значение имеет интерпретация полученных откорректированных результатов. Исследования показали, что скорректированные F-функции имеют глубокий физический смысл, а некоторые могут быть даже проверены по имеющейся избыточной информации. Так, например, скорректированная F-функция мощности хорошо совпадает с пронормированной функцией распределения активной мощности, полученной в работе [85]. То есть, на основе динамической модели уточняется исходное допущение для статической модели о том, что вся мощность пласта будет активной. Таким образом, экспериментальная проверка рассчитанных F-функций позволяет подтвердить правильность разработанных операций и алгоритмов.

По мере накопления геолого-промысловой информации в процессе разработки газового месторождения происходит снижение уровня неопределенности для оценки запасов газа. Поэтому с помощью предложенных авторами рекуррентных соотношений [134] имеется возможность проводить адаптивное уточнение F-функции. На рис.7.5 приведен пример такого динамического уточнения оценки запасов для рассматриваемого месторождения .

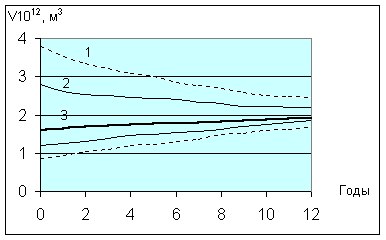
Рис.7.5. Динамическое уточнение оценки запасов для r-уровней 0 - (1); 0,5 - (2); 1 - (3)

Извлекаемые запасы оцениваются аналогично (7.11), только в этом случае соответствующие функции принадлежности характеризуют активно отрабатываемые типы коллекторов и представляют собой нечеткие интервалы с размытой правой границей.

Коэффициент конечной газоотдачи определяется как отношение нечетких величин извлекаемых и балансовых запасов. В качестве примера на рис. 7.6 показана оценка нечеткого коэффициента газоотдачи для рассматриваемого месторождения [28].

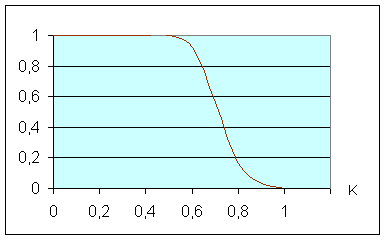
Рис. 7.6. Функция принадлежности для коэффициента газоотдачи

Была проведена проверка устойчивости решений, получаемых при различных видах функций принадлежности. В работах [38, 134] приведены результаты, полученные для F- функций экспоненциального вида, а в [39] - для линейного, а в [135] - для линейного и параболического типа. Сравнение полученных решений показало высокую точность для результирующих точечных оценок, высокую эффективность процедуры коррекции исходных F-функций, которая позволяет обеспечить устойчивость решений и значительно снижает влияние выбранного вида F-функций на конечный результат. Особенность разработанных алгоритмов позволяет использовать корректирующую процедуру для последовательной адаптации F-функций для неточно заданных величин аналогично процедуре Байеса.

В качестве примера проведено сравнение результатов, полученных с использованием прямых и обратных методов и метода LR-чисел [2] с треугольными функциями принадлежности. Решение по объемному методу запишется в виде , а по балансовому методу в виде.

Как показывают расчеты, решения, полученные с применением арифметических операций над LR-числами, достаточно точно аппроксимируются даже LR-числами с функциями принадлежности треугольного вида, однако ошибка полученная в результате применения операции пересечения Заде дает разницу в согласованном решении 10-15%. То есть, аппроксимация треугольными функциями в этом случае дает уже существенное смещение оценки точки максимума результирующей функции. Поэтому при использовании операций с LR-числами необходимо применять более сложные аппроксимирующие функции.

Таким образом, применение теории нечетких множеств для оценивания технологических параметров при наличии в уравнениях неточно заданных величин дает возможность получить количественную характеристику неопределенности оцениваемых параметров и создает основу для принятия обоснованных решений при существовании у исследователя нескольких моделей.

На основе всех предложенных авторами алгоритмов совместно с группой программистов КИВЦ Главтюменгазпрома был разработан и внедрен в промышленную эксплуатацию комплекс программ по расчету и корректировке запасов газа в условиях неопределенности. Результаты расчетов были использованы при составлении "Корректировки к проекту разработки месторождения Медвежье".

[К предыдущей главе].....[К содержанию] ......[К следующей главе]