7.3. Особенности оценки технологических и геолого-промысловых параметров при наличии неточных замеров и моделей

С первых моментов реализации проекта разработки газового (газоконденсатного) месторождения начинается анализ получаемой геолого-промысловой информации и показателей разработки. Первичный, каждодневный анализ процесса разработки месторождения осуществляется геологической службой управления или объединения с центральной научно-исследовательской лабораторией (ЦНИЛ) или цехом научных и производственных работ (ЦНИПР).

Задачи первичного анализа разработки следующие.

1. Обработка и анализ результатов геофизических, газогидродинамических и специальных исследований скважин и пластов.

2. Анализ данных по контролю за разработкой месторождения. Сопоставление и анализ фактических и проектных показателей разработки.

3. Анализ результатов работ по интенсификации добычи газа.

4. Корректирование отдельных положений проекта разработки или доразработки месторождения.

Анализ получаемых результатов позволяет выявить изменения я причины изменений продуктивных характеристик скважин. Анализ данных контроля за разработкой месторождения позволяет установить режим месторождения, характер продвижения воды в пределах отдельных залежей и пластов, степень дренирования месторождения по площади газоносности и мощности.

Сопоставление и анализ фактических и проектных показателей разработки позволяет установить, в частности, причины отклонений между ними. Одним из основных факторов, приводящих к отклонениям между фактическими и проектными показателями разработки, является степень достоверности определения начальных запасов газа в пласте. Поэтому в задачи первичного анализа входят построение зависимости и периодическое уточнение запасов газа. До последнего времени наибольшее распространение при определении запасов газа имеют объемный метод и метод падения пластового давления. В следующих разделах приводится описание указанных методов и их применение для расчетов с нечетко заданными величинами.

При проведении расчетов, оценивании параметров, составлении балансовых отчетов и т. д. Очень часто возникает необходимость работы с неточно заданными величинами. Искусственное введение детерминированных (четких) величин приводит к необходимости проведения многовариантных просчетов с итерационным подбором нечетко или интервально заданных величин. Чаще всего это связано с возможностью проверки конечного результата (небаланс, косвенный замер, субъективное требование к результату – “x должно быть равно приблизительно c” и т. д.). Поэтому точный выбор варьируемых величин сильно затрудняет процесс принятия решения. К тому же, специалиста часто интересуют оценки погрешности полученного результата и точности выполнения установленных планов и заданий.

Многие параметры технологических процессов трудно (а иногда и невозможно) получить путем проведения замеров. Поэтому приходится оценивать их по косвенным измерениям с использованием различных уравнений. Однако, как показывает практика, при проведении расчетов специалисты пользуются в основном детерминированными методами. При этом не учитываются погрешности замеров величин, ошибки, получаемые за счет усреднения, взвешивание некоторых параметров, а для ряда уравнений – и неточность, вносимая при экспертной оценке отдельных величин, то есть априорная информация об этих параметрах может быть недетерминированной (не точечной), а стохастической, лингвистической, нечеткой или интервальной.

Однако получение необходимой стохастической информации о плотностях распределения вероятностей для технологических параметров, особенно в осложненных условиях эксплуатации, на начальных стадиях разработки газовых месторождений не представляется возможным (число точек и замеров параметров недостаточно для статистически обоснованных выводов). Чаще всего для параметров бывают известны лишь интервальные ограничения (то есть заданы минимальное и максимальное значение для каждого параметра), наиболее правдоподобное (среднее, средневзвешенное и т.д.) точечное значение , а иногда – погрешность замера (дисперсия, абсолютная и относительная ошибки и т.д.). Если заданы ,,, то такие величины можно характеризовать треугольной плотностью распределения вероятности, если же задана и величина , то применение операций теории расчетов применяют в основном лишь крайне трудоемкие численные методы (например, метод Монте-Карло). Некоторые параметры могут оцениваться и на основе экспертных оценок. Поэтому наиболее целесообразно в качестве характеристик неточно заданных параметров функций принадлежности использовать значения этих параметров в подмножестве допустимых. В частном случае как функции принадлежности могут выступать и нормализованная плотность распределения вероятности, и функция предпочтения, полеченная на основе экспертного опроса. Операции с нечеткими переменными гораздо проще соответствующих вероятностных операций. В зависимости от способа получения этой информации соответствующие параметры носят объективный или субъективный характер. Нечеткое моделирование является в настоящее время одним из наиболее удачных путей адекватного представления наших объективных и субъективных знаний об объекте, особенно при наличии в уравнении параметров с различными видами неопределенности. В этом случае в уравнении, описывающем объект,

наряду с вектором точечных параметров x имеется и вектор нечетких величин , каждая из которых представляется своим нечетким множеством . Соответственно и вектор оцениваемых параметров в этом случае будет нечетким множеством Y. Тогда функцию принадлежности для при условии независимости нечетких величин можно записать не основе использования обобщенного понятия функции:

(7.6)

где , а – функции принадлежности для параметров . Алгебраические операции над нечеткими величинами проводятся с использованием методов, описанных ранее. Покажем особенности работы с нечеткими величинами на конкретных примерах.

Оценка параметров по прямым измерениям. Рассмотрим вначале влияние погрешности замеров на оценку контролируемой величины. Ошибка измерения считается нечеткой и задается с помощью функции принадлежности, вид которой получают на основе характеристик измерительных приборов.

Наиболее простой случай построения функции принадлежности для допустимых значений оцениваемого параметра - когда выполняется непосредственное его измерение (например, устьевое давление, пластовая температура). При этом для скалярного показания прибора и нечеткой величины погрешности измерения производится алгебраическая операция сложения или умножения в зависимости от того, является ли помеха аддитивной или мультипликативной. Для нахождения результатов алгебраических операций используется прямой аналитический метод.

Пусть, например, температура газа в пласте измеряется с погрешностью 5° С. При этом ошибки измерений считаются аддитивными. На практике можно использовать для погрешности измерений функцию принадлежности треугольного вида, зная лишь интервал допустимых ошибок:

Множество допустимых значений пластовой температуры находится по правилам сложения нечеткой величины со скаляром:

Оценка параметров по косвенным измерениям. Более сложный случай представляет косвенное измерение, когда контролируемая величина рассчитывается с помощью определенных формул. Например, дебит газовой скважины определяется специальным прибором по устьевому давлению и рассчитывается по формуле

где с - постоянная прибора;

P - давление на приборе;

T - абсолютная температура газа на устье;

r- относительная плотность газа по воздуху;

z - коэффициент сжимаемости газа при P и T.

В этой ситуации применение прямого аналитического метода часто приводит к довольно громоздким выражениям, поэтому более удобно для нахождения искомой функции принадлежности использовать обратный численный метод.

Нечеткие функциональные зависимости. ТНМ может быть успешно применена для оценивания погрешности расчета по функциям произвольного вида

Для оценки предельной величины погрешности таких функций обычно применяется формула теории ошибок измерений

. (7.7)

Однако при этом предполагается, что функция имеет непрерывные частные производные по переменным x_iи в случае влияние ошибки Dx_i не учитывается. Использование указанной формулы на практике иногда дает слишком сложные выражения для ошибки Dy. К тому же вычисленная по линеаризованному выражению (7.7), величина Dy является доволно грубой оценкой погрешности функцииf, особенно при наличии больших ошибок замеров параметров x _i.

Авторами совместно с группой сотрудников КИВЦ Главтюменгазпрома разработаны методики и проведены расчеты целого ряда технологических и геолого-промысловых параметров для газовых месторождений севера Тюменской области с использованием теории нечетких множеств и интервального анализа: обработка результатов исследований на стационарных режимах фильтрации - построение нечеткой и интервальной индикаторной кривой с оцениванием соответствующих коэффициентов А и В [39], оценивание нечеткого коэффициента газоотдачи [28], оценивание нечетких запасов газа для газовых месторождений [37, 39, 124], идентификация дебитов газовых скважин [39, 134].

7.4. Обработка индикаторных кривых при неточных измерениях

Одним из распространенных гидродинамических методов изучения газовых скважин является исследование на стационарных режимах фильтрации. Обработка индикаторной кривой традиционными способами сводится к нахождению коэффициентов А и В по графику прямой линии [85]:

, (7.8)

где Q - дебит газовой скважины;

- пластовое и забойное давления;

А, В - коэффициенты фильтрационного сопротивления.

Известно, что в основе метода наименьших квадратов, используемого для оценки параметров, лежат следующие предположения [234]:

1. Независимая переменная не является случайной величиной.

2. Измерения зависимой переменной статистически независимы.

3. Условное распределение у при заданном является нормальным.

4. Дисперсия ошибки измерения равна дисперсии зависимой переменной .

На практике нарушения этих условий обычно заключаются в следующем:

1. независимая переменная является случайной величиной и замеряется с некоторой погрешностью;

2. ошибки измерения не являются статистически независимыми;

3. интервал изменений переменной слишком мал, а ошибки измерения у слишком большие, так что вариация зависимой переменной соизмерима с ошибкой ее измерения;

4. дисперсии переменных

и у могут зависеть от их абсолютной величины.

В общем случае, когда зависимая и независимая переменные - случайные величины, проблема оценивания параметров регрессии практически не разрешима [234], так как получающаяся система уравнений является нелинейной, что затрудняет ее решение в явном виде даже для экспоненциальных функций распределения.

Рассмотрим один из методов оценивания нечетких параметров уравнения (7.8), имея в виду, что могут быть найдены и другие способы оценивания, дающие, например, более узкие допустимые области параметров.

Допустим, исходные величины измеряются с погрешностями 5% для расхода газа и 0,2% - для давления. Используя интервальные операции для вычисления величины у [247], получим, что погрешность ее определения для реальных значений давлений и расходов газа составляет 6,5%. Тогда допустимые множества значений, которые могут принимать параметры и при известных замерах и , можно задать экспоненциальными функциями принадлежности

,

,

где и - максимально допустимые погрешности измерений.

Рассмотрим функцию принадлежности для совместного распределения А и В как отображение результатов n измерений, когда в качестве пересечения берется операция умножения

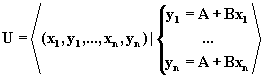
Принимая во внимание взаимную однозначность рассматриваемого отображения и вид исходных функций принадлежности, получаем

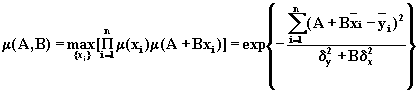(7.9)

Исследовать функцию довольно трудно. Однако можно указать такую функцию , что в области реально допустимых значений коэффициента В выполняется неравенство

.

Для этого достаточно взять значение в знаменателе экспоненты (7.9) заведомо больше максимально допустимого.

Чтобы определить функции принадлежности отдельно для каждого коэффициента, необходимо спроектировать совместную функцию на соответствующие оси:

; (7.10)

,

где ;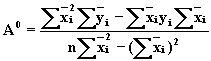

;

;

;

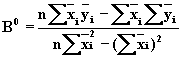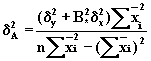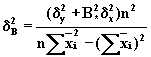С - константа, равная максимальному значению функции .

Из анализа выражений (7.10) следует, что при увеличении числа замеров сокращается допустимый интервал для значений коэффициентов А и В при фиксированном r-уровне.

Таким образом, используя различное число экспериментальных точек, можно вычислить коэффициенты фильтрационного сопротивления с различной степенью точности. Аналогом доверительных интервалов в этом случае являются r-уровневые множества и . Графически такие интервалы для r-уровневых множеств имеют прямолинейные границы.

Для исследования точности расчета коэффициентов А и В рассмотрим обработку индикаторных кривых для одной из скважин месторождения Медвежье. Результаты вычислений приведены в табл.7.1.

Таблица 7.1.

Оценка нечеткости при обработке индикаторных кривых для одной

из скважин месторождения Медвежье

Полученные зависимости (рис.7.2) показывают, что для более надежного определения коэффициентов фильтрационного сопротивления необходимы 6-8 замеров и более широкий диапазон изменений расхода.

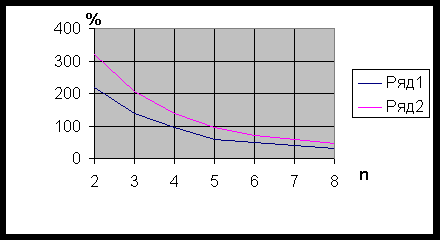
Рис.7.2. График изменения относительной погрешности вычисления коэффициентов А и В ( - ряд 1, - ряд 2).

[К предыдущей главе].....[К содержанию] ......[К следующей главе]