8.7. Расчет и оптимизация режимов работы межпромысловых коллекторов, УКПГ и ДКС с учетом неопределенности

Разработанный комплексный алгоритм расчета и оптимизации системы газодобычи учитывает целый ряд очень важных для практики особенностей:

- возможность расчета отдельных подсистем (коллектора, газосборных сетей УКПГ и т.д.) как элементов иерархической системы управления добычей газа с учетом координирующих нечетких параметров со стороны процесса разработки месторождения, технологического оборудования УКПГ и магистрального транспорта газа;

- возможность проведения расчетов при наличии неопределенности информации;

- создание и возможность расширения базы знаний в экспертной системе для технологов и диспетчерского персонала;

- учет зависимости давлений на выходах УКПГ и выходах МК от расхода газа;

- проведение расчета и оптимизации МК с учетом ДКС с использованием блока расчета КС;

- возможность проведения параметрической (по параметру Е) и структурной идентификации фактического состояния газосборной сети, коллектора и призабойной зоны пласта;

- проведение оптимизационных расчетов при наличии нескольких выходов из коллектора в магистральные газопроводы;

- возможность анализа узких мест и доминирующих ограничений в системе, оценки эффективности проведения ремонтных работ, переключений и изменения режима работы системы газодобычи в том числе и с позиций обеспечения устойчивости функционирования в условиях неопределенности.

Алгоритм оптимизации

С учетом декомпозиции общей задачи управления алгоритм принятия решений в иерархической системе газодобычи (рис. 8.1) запишется следующим образом:

1. С заданной периодичностью (месяц, квартал, год) решается задача прогнозирования пластового давления и построения функций для момента времени на основе алгоритмов, приведенных в главе 7.

2. Для момента времени принимается нечеткое решение на уровне 2 для каждой j-ой УКПГ

; (8.92)

при и с учетом наличия ограничений (8.1) - (8.7) и нечетких ограничений и критериев работы технологического оборудования УКПГ (вопросы построения этих функций подробно рассматривались в работе [127]). В состав УКПГ может входить и ДКС, для моделирования которой используются алгоритмы, описанные в работе [134].

3. Решается задача нечеткой оптимизации 3-го уровня для месторождения в целом

; (8.93)

при , для k МГ с учетом наличия ограничений (8.52) - (8.54) и нечетких координирующих решений со стороны процесса магистрального транспорта газа для каждого r-го МГ. Эти функции используются на региональном уровне для решения задачи распределения отборов газа по группе газовых месторождений.

4. Для получения конкретного четкого управляющего воздействия фиксируется значение отбора газа по месторождению и давления входа в ГКС, при котором выполняются определенные вышестоящим уровнем управления поставки газа и обеспечивается функционирование системы при максимальных значениях функций принадлежности (8.56).

5. С учетом полученных решений аналогично определяются и () и режимы работы межпромыслового коллектора.

6. На основе этих четких решений определяются дебиты газовых скважин и режимы работы газосборных сетей и технологического оборудования УКПГ.

Одним из численных методов реализации этого алгоритма могут быть использованы процедуры главы 5 настоящей работы, главы 5 [134] или главы 4 [30]. В качестве примера в таблицах 8.3, 8.4 приведены результаты расчета режимов, максимизирующих функцию принадлежности для системы газодобычи гипотетического месторождения, аналогичному по большинству параметров месторождению Медвежье.

Таблица 8.3.

Эффективные четкие отборы газа по УКПГ при плановом отборе 236,848 млн.м³/сут.

Таблица 8.4.

Оптимальные отборы газа по скважинам УКПГ2 при входном давлении 7.38 МПа.

201 8.94 1.050 1.100 7.57 0.9857

202 8.97 1.100 0.954 7.52 0.8935

203 9.03 1.050 1.106 7.57 0.9818

204 8.97 0.600 0.735 7.46 0.7228

205 9.04 1.100 0.882 7.50 0.7792

206 8.93 0.650 0.866 7.50 0.4946

207 8.98 0.700 0.749 7.47 0.9692

208 9.00 1.000 1.198 7.60 0.7796

209 8.97 0.750 0.891 7.48 0.2291

210 8.92 0.900 0.989 7.53 0.9400

211 8.76 0.800 0.806 7.48 0.9997

212 8.90 0.550 0.809 7.48 0.2439

213 8.89 0.700 0.694 7.45 0.9995

214 8.94 0.600 0.834 7.49 0.3785

215 8.94 0.400 0.806 7.48 0.1014

216 9.05 0.950 1.127 7.58 0.8013

217 8.91 0.450 0.581 7.43 0.5809

218 8.91 0.700 0.839 7.49 0.7777

219 9.02 1.000 1.322 7.65 0.5165

220 8.81 0.500 0.886 7.50 0.0224

221 8.99 0.700 0.908 7.51 0.5691

222 9.05 0.350 0.379 7.40 0.9569

223 9.12 0.900 1.455 7.71 0.0886

224 9.08 0.726 0.784 7.48 0.9606

Разработанный численный алгоритм оптимизации реализует особенность иерархической структуры, согласно которой решение на нижестоящем уровне не определяется в окончательном виде до тех пор пока не решена проблема на вышестоящем уровне. При этом концепция нечетких множеств позволяет учесть оптимальность работы каждой подсистемы.

Нечеткость принимаемых решений на каждом уровне управления вплоть до самого верхнего уровня, где принимается окончательное решение, позволяет осуществить оптимальное управление иерархической системой газодобычи. На основе предложенного алгоритма созданы соответствующие комплексы программ. Проводимые с помощью этих комплексов расчеты показали высокую устойчивость, хорошую скорость сходимости и хорошую точность предложенных алгоритмов.

8.8. Нечеткое автоматическое регулирование

В случае, когда процесс принятия решений по управлению технологическим объектом осуществляется оператором, возникает необходимость моделирования этого решения и оценки его точности и эффективности. Моделирование может быть осуществлено с использованием теории нечетких множеств [288, 289].

В этом случае нечеткая логика используется для исследования и формализации эвристических правил управления, которыми пользуется оператор для регулирования сложных технологических процессов добычи, подготовки и транспорта природного газа. И нечеткий логический регулятор является лингвистической моделью стратегии человека-оператора и может, таким образом, служить моделью решающего блока.

Регуляторы с нечеткой логикой обеспечивают повышенную надежность систем, позволяют учитывать ограничения по устойчивости, полученные с помощью теории Ляпунова в применении к дискретным системам [300]. Этот подход не требует наличия математических моделей объекта управления.

Покажем, каким образом можно описать стратегию управления оператора, используя нечеткие и плохо определенные понятия естественного языка [134, 262].

Лингвистическая информация может быть получена при изучении реакции оператора в различных ситуациях, а стратегии управления выражены в виде лингвистических решающих правил в форме:

Если "увеличение давления большое", то "частично уменьшить расход", иначе, если "увеличение давления небольшое", то "незначительно уменьшить расход", и т.д.

Таким образом, базовыми понятиями являются нечеткие понятия "увеличение давления" и "уменьшение расхода", а взаимосвязь между ними представляется в виде композиционного правила вывода

(8.94)

где - нечеткие понятия, являющиеся суждениями о выходе и входе объекта соответственно. Функция принадлежности соответствует нечеткому условному оператору S, где нечеткое подмножество А определено на области суждений Х, а нечеткое подмножество В на Y:

. (8.95)

Сложная система поведения описывается совокупностью таких нечетких инструкций с использованием операций "ИЛИ"

(8.96)

с функцией принадлежности

(8.97)

В таком виде стратегия поведения человека может быть введена в ЭВМ. Основой для принятия решения при известном входе и заданном отношении между нечеткими множествами (4) является композиционное правило вывода Заде [98]:

. (8.98)

При управлении конкретным процессом вход может быть и точечным (четким) . В этом случае композиционное правило вывода упрощается, так как вход можно интерпретировать как нечеткий вход с функцией принадлежности , везде равной нулю, за исключением точки измерения , где она равна единице

. (8.99)

Для принятия четкого решения необходимо выбрать такое управление , которое максимизирует результирующую функцию принадлежности

. (8.100)

Дадим описание принципов построения и работы нечеткого алгоритма для простейшего процесса (один вход - один выход), в котором каждая инструкция i связывает нечеткое понятие давления p с нечетким понятием расхода q через их функции принадлежности

. (8.101)

Для более сложных случаев (несколько входов - один выход), например, при наличии еще и нечетких понятий температуры, точки росы и т.д., используется более сложные формы нечетких инструкций

(8.102)

с функциями принадлежности

. (8.103)

Для случая (8.101) четкое значение расхода может быть найдено по следующему алгоритму при измеренном значении давления :

1. Для каждой инструкции i определяются степени принадлежности давления

. (8.104)

2. Находятся функции принадлежности, определяющие нечеткое понятие расхода для каждой инструкции

, (8.105)

а затем полное нечеткое понятие расхода:

. (8.106)

3. Вычисляется четкое управляющее воздействие , обеспечивающее максимум функции принадлежности :

. (8.107)

Начальное построение функций принадлежности может быть выполнено с использованием экспоненциальных функций с дальнейшей их адаптацией по критерию качества управления с помощью полученной модели. Данная модель может быть использована при создании системы автоматического управления функционированием технологического объекта. Это обусловлено тем, что существующие системы автоматического управления не учитывают сложные нелинейности, погрешность замера параметров и транспортные запаздывания реальных объектов.

Для управления возможно построение нескольких типов алгоритмов, которые различаются по виду используемой информации: измеряется только отклонение от заданного значения, отклонение и значение его первой производной и т.д. Конкретный тип алгоритма выбирается для каждого случая, исходя из анализа различных стратегий.

Возможные подходы к построению нечетких алгоритмов, сравнительный их анализ и сопоставление с классическими регуляторами приведены в работе [289]. Там же отмечаются преимущества нечетких алгоритмов: высокая скорость отклика в сочетании с такой же точностью, как у промышленных регуляторов, существенно нелинейный характер нечеткого управления.

Сравнение результатов прямого цифрового управления и нечеткого управления, проведенные во многих работах по применению теории нечетких множеств показали, что нечеткое управление проще и эффективнее обычно применяемых классических методов [225, 290]. В качестве примера можно привести наиболее характерный результат сравнительного анализа прямого цифрового (1) и нечеткого (2) управления для экспериментальной установки при управлении давлением на ее выходе (рис.8.6.) [225].

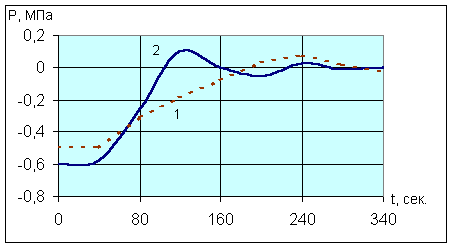
Рис. 8.6. Прямое цифровое управление (гафик 1) и нечеткое управление (график 2).

В работе [348] описывается самоорганизующийся нечеткий регулятор (СНР), имеющий иерархическую структуру и состоящий из двух алгоритмов: в нижней цепи имеется регулятор с алгоритмом, построенным на нечеткой логике; в верхней цепи имеется самообучающийся регулятор, с алгоритмом обучения, приспосабливающим изменение качества системы к изменению внешних условий. СНР функционально разделяется на 6 блоков: квантователь, регулятор, интерпретатор, матрица модели, критерий качества, модификатор [348].

Описываются назначение каждого блока и алгоритмы с указанием нечетких множеств и их функций принадлежности. Приводится закон установки оптимальных параметров регулятора. Показывается, что чувствительность СНР к изменению параметров объекта аналогична пропорционально-интегральному регулятору.

Описанные алгоритмы могут быть широко применены в газовой промышленности для регулирования и управления различными технологическими процессами при непосредственном цифровом управлении с применением микро ЭВМ или при выдаче рекомендаций оператору в режиме диалога.

Нечеткие алгоритмы могут использоваться при управлении нестационарным процессом добычи и транспорта газа, а также для управления процессом подготовки природного газа. Для управления этим процессом применение нечетких алгоритмов особенно эффективно, так как отсутствие датчиков для замеров ряда параметров, по значению которых и принимаются решения (например, о расходе диэтиленгликоля), приводит к тому, что входные величины оцениваются с помощью аналитических датчиков приближенно и по сути являются нечеткими.

В связи с необходимостью реализации этого класса нечетких алгоритмов на микропроцессорной технике большое значение приобретают проблемы выбора формы представления в памяти микропроцессорной системы лингвистических алгоритмов и семантики терм-значений [51].

Анализ двух видов интерпретаций: реляционной, основанной на композиционном правиле вывода Заде [98], и ситуационной, базирующейся на вычислении степени близости анализируемой ситуации с эталонными и определении решения, соответствующего наиболее близкой эталонной ситуации, показало, что при суммарном числе входных и выходных переменных менее четырех наиболее эффективна реляционная интерпретация. Если суммарное число переменных больше четырех, должна использоваться ситуационная интерпретация [51].

Подобная концепция построения решающих правил использована системе комплексной автоматизации производства фирмы Hitachi (Япония) [347]. Для этой системы разработан специальный пакет программного обеспечения SCD, в котором заложен метод управления в соответствии с набором правил. Благодаря этому пакету удается формировать управляющую программу не на языках программирования ЭВМ (например, Паскаль или Бейсик), а в виде набора правил "если - то", отражающих ограничения на производственный процесс. Опыт и знания операторов и мастеров преобразуются в правила интерактивным редактором. Накопленные правила хранятся в памяти контроллера в виде базы знаний. Блок формирования управляющих воздействий принимает решение о том, какое действие нужно предпринять в процессе выполнения процедуры сравнения состояний, описание которых имеется в виде сигналов о событиях в производственном процессе.

В целом данный подход обеспечивает [347]:

1. Сокращение трудозатрат на разработку прикладного программного обеспечения в среднем в 3 раза.

2. Принципы построения управляющих программ позволяют легко работать с ним операторам, не знающим программирования.

[К предыдущей главе].....[К содержанию] ......[К следующей главе]