8.5. Алгоритм расчета сетевого коллектора, имеющего древовидную подструктуру
Пусть газосборная сеть задается в виде связного ориентированного графа без петель. Входами сети являются K установок комплексной подготовки газа, а выходами - M головных компрессорных станций. Под узлами (вершинами) графа понимаются начальные и конечные точки линейных участков, все точки разветвления или объединения потоков газа, точки поступления и отбора газа. Под ребром графа понимается линейный участок, соединяющий две вершины графа. Предположим, что полученный граф имеет N узлов и L ребер.
Стационарное движение газа по газосборной сети описывается системой нелинейных алгебраических уравнений (8.7)-(8.8). В некоторых реальных случаях такая система содержит 200-300 и более неизвестных. Это приводит к необходимости решения задач большой размерности и предъявляет определенные требования к быстродействию и объему оперативной памяти.
Рассматриваемый итерационный метод расчета максимально учитывает специфику реальных структур коллектора. Как правило, в них выделяются такие элементы, как технологические нитки и перемычки. Основная роль в межпромысловом транспорте газа принадлежит технологическим ниткам, в то время как перемычки играют вспомогательную роль. Обычно технологические нитки образуют существенно более простую структуру, приводимую (путем удаления перемычек) к древовидному подграфу.
Итерационная процедура включает в себя расчет дерева - учет перемычек. Для расчета дерева нет необходимости использовать общие методы решения систем, а можно воспользоваться приемами типа прогонки. При этом, требования к конфигурации вычислительных средств оказываются минимальными, а число операций линейно зависит от количества узлов дерева. Удаленные ребра исходного графа (перемычки) заменяются граничными (концевыми) условиями в виде линейной комбинации расхода газа по перемычке и давления в узле.
Предполагается, что исходные концевые условия задаются в таком же виде. Последнее обстоятельство является естественным в реальных задачах: обычно на выходе установки комплексной подготовки газа, подающей газ в коллектор, технологически имеет место зависимость между расходом и давлением газа, которая может быть линеаризована, Условия постоянства расхода или давления также могут рассматриваться как частные случаи линейной зависимости.
После расчета дерева граничные условия пересчитываются из условий обеспечения минимальной невязки для каждой перемычки. Соответствующий алгоритм пересчета обеспечивает сходимость итерационного процесса, в том числе и для процессов транспортировки, описываемых нелинейными соотношениями. Более того, при несущественных изменениях алгоритм может использоваться и для расчета нестационарных процессов.
Для протяженных систем межпромыслового транспорта газа нестационарность процессов может оказывать существенное влияние. Она обусловлена в основном неравномерным характером газопотребления, переключениями на установках комплексной подготовки газа, ремонтными работами и другими переключениями в схеме межпромыслового коллектора. Отсутствие возможности точного прогнозирования процессов газопотребления, большая погрешность технологической информации приводит к высокой неопределенности обстановки при принятии оперативных решений. Применение в процессе принятия решений лишь стационарных моделей приводит к значительным ошибкам, ухудшает эффективность применяемых решений и охватывает лишь в малой степени круг задач, решаемых диспетчерской службой. Поэтому возникает потребность создания имитационных и оптимизационных моделей для принятия решений по контролю и управлению нестационарным процессом межпромыслового транспорта газа.
В случае, когда колебания во времени давления, расхода и температуры достаточно малы, нестационарность режима может быть представлена как нечеткость состояния процесса и задана соответствующими функциями принадлежности [26]. Если степень нестационарности процесса велика, то возникает необходимость использования в качестве модели линейного участка формулы нестационарного режима транспорта газа. Чаще всего для расчетов неустановившегося режима делается допущение об его изотермичности, что позволяет описать его нелинейной системой дифференциальных уравнений в частных производных [26]. В качестве модели могут использоваться и другие, например, более упрощенные формулы расчета нестационарного режима.
В целом алгоритм координации режимов работы установок комплексной подготовки газа и линейных участков остается таким же, как и при стационарном режиме. Например, при нестационарном газопотреблении при необходимости минимизации отклонений от заданного режима в определенных точках (на входе в головную компрессорную станцию, на выходах установок комплексной подготовки газа и т.д.) задается допустимый интервал колебаний давления, расхода газа и задачей системы управления является соблюдение этих ограничений. Процедура корректировки режимов в случае нарушения ограничений или выхода за трубку допустимых для коллектора траекторий аналогична корректировке для стационарного режима, однако более длительна ввиду сложности модели линейного участка.
При необходимости расчета переходного режима в межпромысловом коллекторе при отключении установок комплексной подготовки газа, линейных участков, аварии, проведении ремонтных работ сначала рассчитывается пределный стационарный режим, к которому придет система. Затем определяется сам процесс перевода коллектора из начального состояния в предельное стационарное состояние с учетом имеющихся ограничений в системе.
Некоторое усложнение алгоритма расчета позволяет получать матрицы взаимозависимостей между давлениями и расходами на концах дерева, а значит и сети. Для этого оказывается необходимой лишь соответствующая линеаризация соотношений, описывающих процесс транспортировки газа по линейному участку. Использованы могут быть линейная интерполяция и аппроксимация на базисе заданных режимов или разложения в ряды Тейлора.
Аналогичные возможности имеются и для расчета коэффициентов влияния параметров линейных участков (например, их гидравлических сопротивлений) на получаемые решения. Это дает возможность разработки алгоритмов идентификации газосборной сети, что является весьма важным при функционировании системы управления технологическими процессами промысла.
Анализ численных экспериментов показывает удовлетворительную сходимость итерационного процесса, что позволяет использовать данный метод для моделирования стационарных изотермических, неизотермических и нестационарных процессов межпромыслового транспорта газа, а также для принятия оперативных диспетчерских решений и выбора оптимальных режимов работы межпромыслового коллектора.
Рассмотренные методы расчета и оптимизации позволяют диспетчерским службам промысла оперативно рассчитывать необходимые технологические показатели и выбирать оптимальный режим работы межпромыслового коллектора в аварийных ситуациях, при проведении ремонтных работ и планировании развития систем газодобычи.
Оптимизационные задачи для приведенных выше критериев максимизации добычи газа и давлений газа на выходах МК могут быть решены на основе метода линейной аппроксимации с применением теории чувствительности. Анализ многолетней эксплуатации программ оптимизации и расчетов межпромысловых коллекторов месторождений Медвежье и Уренгойское в Тюменском КИВЦ концерна "Газпром" показал хорошую сходимость и приемлемую для практики точность расчетов. Однако все эти детерминированные методы слабо приспособлены для принятия решений в иерархических системах управления и в условиях неопределенности.
Таким образом, необходимость рассмотрения системы газодобычи как многоуровневой, многоцелевой, а также наличие в системе различных видов неопределенности обусловили создание нового алгоритма на базе теории многоуровневых иерархических систем и теории нечетких множеств.
8.6. Построение допустимых областей функционирования технологических комплексов
Рассмотрим подробно проблему нечеткой координации в многоуровневых иерархических системах. Особое значение приобретает для этих систем вопрос об агрегировании моделей нижестоящих подсистем при формировании модели вышестоящей подсистемы. Иногда вопросы агрегирования решаются излишне примитивно. Например, модель КС строится укрупненно (через мощность агрегатов КС и т.д.), при этом допустимыми становятся режимы, неприемлемые с точки зрения отдельных ГПА. Таким образом, нельзя не учитывать ограничения и технологически предпочтительные режимы, которые даются более детальными моделями. Если эти ограничения учитываются в агрегированной модели вышестоящего уровня, то такое укрупнение можно считать объективным.
Любой элемент
системы транспорта газа будем
описывать шестью переменными,
полностью определяющими его
состояние – расход газа ![]() ,
температура Т и давление
,
температура Т и давление ![]() на входе
и выходе элемента:
на входе
и выходе элемента:
![]() (8.60)
(8.60)
При стационарном
течении газа, отсутствии
потребления газа и попутных
отборов внутри элемента ![]() .
Элементами нашей системы являются
ГПА и линейные участки (ЛУ), из
которых могут образовываться более
сложные системы (например, группы
последовательно и параллельно
соединенные ГПА, КС, КС с
прилегающим к ней ЛУ, МГ в целом).
Однако эти более сложные системы
также будут однозначно
характеризоваться вектором
состояния (8.60).
.
Элементами нашей системы являются
ГПА и линейные участки (ЛУ), из
которых могут образовываться более
сложные системы (например, группы
последовательно и параллельно
соединенные ГПА, КС, КС с
прилегающим к ней ЛУ, МГ в целом).
Однако эти более сложные системы
также будут однозначно
характеризоваться вектором
состояния (8.60).
Один и тот же
вектор состояния для любого
элемента может быть реализован с
помощью различных управляющих
воздействий (частота вращения вала
нагнетателя, перепуск и
дросселирование газа, схемы
включения ГПА и т. д.), поэтому
возникает задача оптимизации
режима работы элемента в рамках
заданного вектора состояния. Такая
задача будет решена далее, а пока
нас интересует лишь допустимость
решений и просто существование
управления, реализующего этот
режим, то есть ![]() при допустимости с
технологических позиций режима
при допустимости с
технологических позиций режима ![]() для
элемента, в противном случае
для
элемента, в противном случае ![]() .
.
Вектор состояния
элемента включает в себя вектор
входных ![]() и вектор выходных
и вектор выходных ![]() параметров,
то есть
параметров,
то есть ![]() .
.
Обозначим – ![]() и
и ![]() множества
выходных и входных параметров
элемента, а
множества
выходных и входных параметров
элемента, а ![]() - множество состояний
элемента.
- множество состояний
элемента.
При проведении расчетов возникает необходимость временной фиксации некоторых входных и промежуточных переменных и соответствующих выходных величин. Это временно фиксированные в теории сжатых множеств носят название параметров и через них осуществляются связь и координация решений подсистем.
Пользуясь леммой
с параметрической декомпозиции
теории сжатых множеств, построим
сжатое множество допустимых
режимов ![]()
![]() ;
;
![]() .
(8.61)
.
(8.61)
Тогда
![]() ,
(8.62)
,
(8.62)
где ![]() -
однозначная скалярная функция,
отображающая z на
линейно-упорядоченное множество П.
-
однозначная скалярная функция,
отображающая z на
линейно-упорядоченное множество П.
В случае иного
задания функции ![]() сжатое множество
сжатое множество ![]() может
содержать только состояния
может
содержать только состояния ![]() ,
доставляющее максимальные
значения функции
,
доставляющее максимальные
значения функции ![]() , или за счет введения
оценки состояния при различных
управлениях позволяет выбирать
вектор управления, доставляющий
максимум оценочной функции при
любом допустимом векторе
состояния.
, или за счет введения
оценки состояния при различных
управлениях позволяет выбирать
вектор управления, доставляющий
максимум оценочной функции при
любом допустимом векторе
состояния.
Для удобства записи основных операций соединения элементов транспорта газа введем следующие обозначения:
![]() (8.63)
(8.63)
Соответственно ![]() -
множество входных давлений и
температур элемента;
-
множество входных давлений и
температур элемента; ![]() -
множество входных расходов газа;
-
множество входных расходов газа; ![]() -
множество выходных давлений и
температур;
-
множество выходных давлений и
температур; ![]() - множество выходных
расходов газа. Тогда
соответствующие сжатые множества
входных
- множество выходных
расходов газа. Тогда
соответствующие сжатые множества
входных ![]() и выходных
и выходных ![]() параметров состояний
элемента будут выглядеть следующим
образом:
параметров состояний
элемента будут выглядеть следующим
образом:
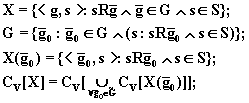 (8.64)
(8.64)
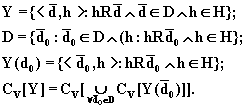 (8.65)
(8.65)
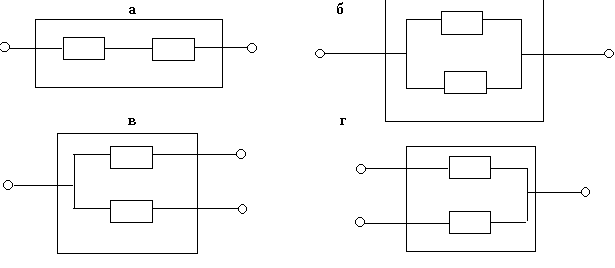 Рис. 8.5.
Возможные соединения подсистем в
систему:
Рис. 8.5.
Возможные соединения подсистем в
систему:
а – последовательное; б – параллельное; в – при разделении материальных потоков; г – соединение при слиянии материальных потоков
Теперь на основе этих процедур получения сжатых множеств состояния элементов можно ввести все операции соединения элементов, необходимых для расчета и оптимизации режимов работы МГ: 1) последовательное соединение элементов; 2) параллельное соединение элементов; 3) разделение потоков газа для элементов; 4) слияние потоков газа для элементов.
Описание этих операций проведем в терминах сжатых множеств. Случай соединения двух элементов легко распространяется на n элементов путем последовательного применения элементарных операций.
Последовательное соединение элементов характеризуется тем, что вход последующего элемента является выходом предыдущего. Это накладывает дополнительные ограничения на режимы работы обоих элементов при согласовании допустимых областей для входных и выходных параметров.
Рассмотрим два последовательно соединенных элемента (рис.8.5, а). Как мы видим, для последовательного соединения
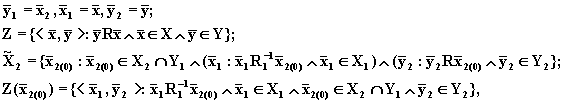 (8.66)
(8.66)
где ![]() - точное
значение
- точное
значение ![]() . Тогда
. Тогда
![]() (8.67)
(8.67)
Очевидно, что сжатые множества входных X и выходных Y параметров последовательного соединения определяются следующим образом:
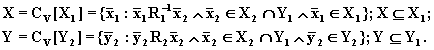 (8.68)
(8.68)
С учетом ограничений последовательного соединения сжатые множества элементов, участвующих в соединении, примут вид:
![]() (8.69)
(8.69)
Параллельное
соединение элементов
характеризуется наличием
одинаковых значений для входных ![]() и
выходных
и
выходных ![]() параметров для обоих
элементов:
параметров для обоих
элементов: ![]()
Расход газа через
систему из двух элементов равен
сумме расходов через два элемента
(рис.8.5, б) ![]() , а температура выхода
системы есть функция от температур
выхода двух элементов. Для
упрощения выкладок без снижения
общности результатов предположим,
что
, а температура выхода
системы есть функция от температур
выхода двух элементов. Для
упрощения выкладок без снижения
общности результатов предположим,
что ![]() и
и ![]() . Тогда
. Тогда
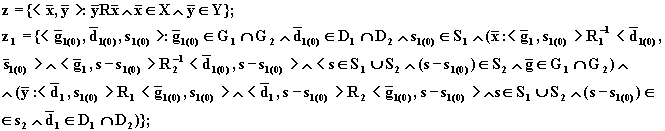 (8.70)
(8.70)
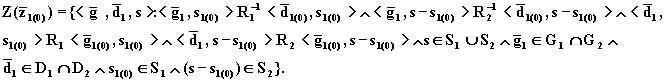 Отсюда
Отсюда
![]() (8.71)
(8.71)
Для параллельного соединения сжатые множества для входных и выходных параметров примут вид:
![]() (8.72)
(8.72)
Сжатые множества для элементов с учетом ограничений параллельного соединения будут определяться следующими выражениями:
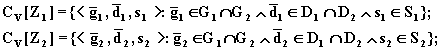 (8.73)
(8.73)
Разделение потоков газа для элементов. При операции разделения согласуют элементы по входным параметрам (рис.7, в):
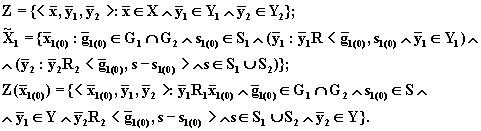 (8.74)
(8.74)
Отсюда, учитывая лемму параметрической декомпозиции,
![]() (8.75)
(8.75)
Сжатые множества входных X и выходных Y параметров для этого вида соединения запишутся следующим образом:
 (8.76)
(8.76)
Тогда сжатые множества элементов примут вид:
![]() (8.77)
(8.77)
При слиянии потоков газа для элементов, при котором происходит согласование для выходных параметров(рис.8.5, г):
 (8.78)
(8.78)
С учетом леммы параметрической декомпозиции сжатое множество для системы запишется в виде
![]() (8.79)
(8.79)
Для входных X и выходных Y параметров сжатые множества запишутся так:
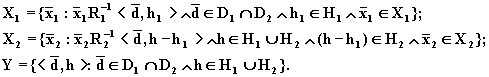 (8.80)
(8.80)
Сжатые множества элементов примут вид:
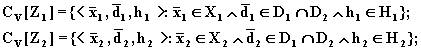 (8.81)
(8.81)
В связи с тем, что для системы газоснабжения сжатыми множествами практически являются допустимые интервалы изменения параметров, для численной реализации предложенных операций и нахождения носителей нечетких множеств применяются операции интервального анализа.
Если на интервалах изменения параметров заданы функции принадлежности, то для построения функций принадлежности всей системы в целом, анализа и принятия решений могут быть использованы операции теории нечетких множеств.
Используя введенное с помощью теории сжатых множеств понятие трубки допустимых режимов и трактуя интервалы допустимых режимов как носителей нечетких множеств, можно с помощью теории нечеткости решать более сложные оптимизационные задачи.
Для композиционных операций большое значение приобретает необходимость построения обобщенных характеристик подсистем, сохраняющих наиболее существенные их свойства, которые требуются учесть при принятии решений на наиболее высоких уровнях управления. При строгом введении такой операции необходимо допущение, что определение задачи является неполным, то есть, что сжатое множество является нечетким. Сжатое множество может быть нечетким в результате того, что на множестве X заданы нечеткие ограничения, цели или сама модель подсистемы является нечеткой.
Покажем, как можно формировать нечеткие модели элементарных звеньев системы и строить агрегированные нечеткие модели при различных схемах включения подсистем с использованием композиционного правила вывода Заде [98].
Нечеткие модели элементарных звеньев системы.
Используя обозначение для элементов системы и учитывая активный характер некоторых звеньев, для стационарного режима при принятии решений в момент t модель любого звена А системы газоснабжения можно описать уравнением вида
![]() (8.82)
(8.82)
где для нашего
случая ![]() и
и ![]() - нечеткие векторы
разрешенных состояний элемента на
выходе и входе соответственно;
- нечеткие векторы
разрешенных состояний элемента на
выходе и входе соответственно; ![]() -
управляющие воздействия в момент t (степень сжатия, число
оборотов ГПА, диаметр штуцера
-
управляющие воздействия в момент t (степень сжатия, число
оборотов ГПА, диаметр штуцера ![]() и т.п.).
Функциональная связь для
элементарных подсистем
и т.п.).
Функциональная связь для
элементарных подсистем ![]() принимается четкой. Подсистеме А в
каждый момент t можно
поставить в соответствие нечеткое
множество с функцией
принадлежности к подмножеству
допустимых режимов
принимается четкой. Подсистеме А в
каждый момент t можно
поставить в соответствие нечеткое
множество с функцией
принадлежности к подмножеству
допустимых режимов ![]() . При
фиксированных значениях
. При
фиксированных значениях ![]() и
и ![]() согласно принципу оптимальности
естественно выбирать такое
управление
согласно принципу оптимальности
естественно выбирать такое
управление ![]() , для которого функция
принадлежности принимает
максимальное значение, то есть
, для которого функция
принадлежности принимает
максимальное значение, то есть
![]() .
(8.83)
.
(8.83)
Таким образом,
дискретизируя множество входных и
выходных параметров, можно
построить нечеткое дискретное
множество для элемента, причем
каждому возможному состоянию
элемента ставится в соответствие
степень его принадлежности к
подмножеству допустимых (по
состоянию) и эффективных (по
управлению) режимов работы ![]() . Такую нечеткую
оптимизацию можно проводить при
наличии целевой функции у элемента
(например, в результате
предварительной декомпозиции)
независимо от решений на
вышестоящих уровнях.
. Такую нечеткую
оптимизацию можно проводить при
наличии целевой функции у элемента
(например, в результате
предварительной декомпозиции)
независимо от решений на
вышестоящих уровнях.
В нашем случае
таким критерием служит минимум
затрат на обеспечение требуемого
выхода ![]() при заданном
при заданном ![]() . Запишем
соотношения для различных видов
соединения двух элементарных
подсистем (для n
подсистем данная процедура
принимается последовательно (n-1
раз):
. Запишем
соотношения для различных видов
соединения двух элементарных
подсистем (для n
подсистем данная процедура
принимается последовательно (n-1
раз):
Последовательное соединение двух подсистем А и В в систему С может быть записано следующим образом:
![]() (8.84)
(8.84)
или, так как ![]()
![]() (8.85)
(8.85)
При отсутствии отбора газа непосредственно от элементов А и В
![]() (8.86)
(8.86)
т.е. значение
вектора промежуточных параметров ![]() должны
быть выбраны такими, чтобы при
фиксированных значениях входа и
выхода для системы С
обеспечивалось максимально
возможное значение системы
принадлежности для этого режима.
должны
быть выбраны такими, чтобы при
фиксированных значениях входа и
выхода для системы С
обеспечивалось максимально
возможное значение системы
принадлежности для этого режима.
Так как режимы работы элементов выбраны оптимальным образом, то и системный режим будет иметь максимальную функцию принадлежности на всей области возможных режимов.
Параллельное соединение двух подсистем А и В в систему С может быть записано как
![]() (8.87)
(8.87)
или, так как ![]() ,
, ![]() ;
; ![]()
![]()
![]() и режимы (особенно для
однотипных элементов) будут
различаться незначительно по
температурному режиму, можно
принять
и режимы (особенно для
однотипных элементов) будут
различаться незначительно по
температурному режиму, можно
принять ![]() и
и
![]() (8.88)
(8.88)
Максимизация по ![]() записана чисто формально, так как
записана чисто формально, так как ![]() рассчитывается через
рассчитывается через ![]() . При
отсутствии потребления газа
элементами
. При
отсутствии потребления газа
элементами ![]() Тогда
Тогда
![]() (8.89)
(8.89)
Это означает, что
распределение потоков газа между
элементами А и В должно быть
выбрано таким образом, чтобы
обеспечивалось максимально
возможное значение степени
принадлежности этого режима.
Предположение о незначительных
различиях температурных режимов
сделано только для упрощения
абстрактных записей. В комплексе
программ имеется специальный блок
расчета ![]() и коррекции функций
принадлежности.
и коррекции функций
принадлежности.
Процедура разделения потоков газа для элементов будет выглядеть следующим образом:
![]() (8.90)
(8.90)
Процедура слияния потоков газа для элементов в некотором смысле похожа на параллельное соединение и запишется в виде:
![]() (8.91)
(8.91)
С помощью введенных операций может быть описана любая газотранспортная и газодобывающая система (лучевая, кольцевая, сетевая и древовидная). В таком обобщенном виде могут задаваться как активные (ГПА, КС), так и пассивные (ЛУ) элементы и подсистемы.
В общем случае функции принадлежности для нестационарных режимов могут зависеть от времени как от параметра. Необходимость использования понятия нечеткого решения обусловлена не только наличием неопределенности, но и невозможностью принятия четкого решения на любом участке до полного согласования режимов его работы с режимами других ЛУ и КС и режимами работы потребителей. В виде функций принадлежности могут быть заданы и учтены в процессе принятия решений нечеткие ограничения и граничные условия.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]