КОНТРОЛЬНЫЕ ЗАДАНИЯ

1. Случайная величина X равномерно распределена в интервале от 1 до 7, а плотность распределения вероятности случайной величины Y равна f(y)=ay² в интервале от 0 до 5. При этом случайные величины X и Y являются независимыми. Вычислить математическое ожидание и дисперсию суммы этих случайных величин Z = X + Y.
2. Плотность распределения вероятности случайной величины X равна f(x)=ax в интервале от 1 до 5, а случайная величина Y равномерно распределена в интервале от 0 до 5. При этом случайные величины X и Y являются независимыми. Вычислить математическое ожидание и дисперсию разности этих случайных величин Z = X - Y.
3. Случайные величины X и Y являются независимыми. Требуется доказать, что дисперсия суммы этих случайных величин равна сумме их дисперсий.
4. Случайная величина X имеет плотность распределения вероятности 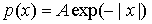. Найти коэффициент A, математическое ожидание и построить функцию распределения случайной величины X.
5. Случайная величина X имеет плотность распределения вероятности f(x)=ax в интервале от 0 до 2. Построить функцию распределения случайной величины X, а также вычислить математическое ожидание и дисперсию.
6. Случайная величина X имеет плотность распределения вероятности следующего вида:
   f(х)=сx, при x в интервале от 0 до 2;
   f(х)=с, при других х , где 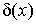- дельта-функция.
   Вычислить математическое ожидание случайной величины X, дисперсию и функцию распределения вероятности.
7. Случайная величина X имеет плотность распределения вероятности следующего вида:
   f(х)=0.1x, при x в интервале от 0 до 1;
   f(х)=, при других х , где 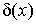- дельта-функция.
   Вычислить математическое ожидание случайной величины X, дисперсию и функцию распределения вероятности.