8. ЗАДАНИЯ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ

1. Написать программный датчик случайной величины с равномерной плотностью распределения вероятности в интервале от -2 до 7. Затем написать вызывающую функцию, которая выводит на график две экспериментальные зависимости плотности распределения вероятности. Отличием этих двух зависимостей является различное число экспериментов (для построения одной зависимости используется значительно большее число экспериментов).

2. Необходимо смоделировать реализацию случайной величины Х, которая может принимать 7 значений 5, 7, 17, 19, 21, 25, 55 со следующими вероятностями:
Р(Х=5)=0.01, Р(Х=7)=0.05, Р(Х=17)=0.3, Р(Х=19)=0.3,
P(X=21)=0.3, P(X=25)=0.02, P(X=55) = 0.02.

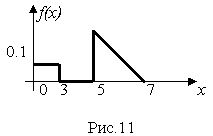
3. Построить датчик случайной величины с плотностью распределения вероятности, показанной на рис.11. Путем проведения статистического моделирования построить график плотности распределения вероятности величины, формируемой датчиком.

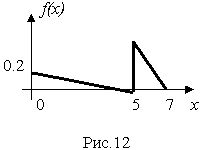
4. Построить датчик случайной величины с плотностью распределения вероятности, показанной на рис.12. Путем проведения статистического моделирования построить график плотности распределения вероятности величины, формируемой датчиком.

5. Построить экспериментальную кривую плотности распределения вероятности случайной величины Y, которая определяется суммой двух случайных величин:

при этом Х имеет плотность распределения вероятности f(x)=ax в интервале , а Z имеет плотность распределения вероятности f(z)=bz² в интервале .

6. Построить экспериментальную кривую плотности распределения вероятности случайной величины Y, которая выражается разностью двух случайных величин:

при этом Х имеет плотность распределения вероятности f(x)=ax в интервале , а Z имеет плотность распределения вероятности f(z)=bz² в интервале .

7. Построить экспериментальную кривую плотности распределения вероятности случайной величины Y, которая задается суммой двух случайных величин:

при этом Х имеет гауссовскую плотность распределения вероятности с математическим ожиданием 3 и дисперсией 2, а Z имеет равномерную плотность распределения вероятности в интервале от 5 до 7.

8. Построить экспериментальную кривую плотности распределения вероятности случайной величины Y, которая определяется суммой трех независимых случайных величин:

при этом Х, Y, Z имеют одинаковую плотность распределения вероятности, соответствующую рис.12. Вывести на график одновременно с кривой плотности распределения вероятности график гауссовской плотности распределения. Математическое ожидание у гауссовской случайной величины равно математическому ожиданию величины Y, а дисперсия гауссовской случайной величины равна дисперсии случайной величины Y.

9. Построить экспериментальную кривую плотности распределения вероятности случайной величины Y, которая определяется суммой трех независимых случайных величин:

при этом Х, Y, Z имеют равномерную плотность распределения вероятности в интервале от 0 до 5. Вывести на график одновременно с кривой плотности распределения вероятности график гауссовской плотности распределения. Математическое ожидание у гауссовской случайной величины равно математическому ожиданию величины Y, а дисперсия гауссовской случайной величины равна дисперсии случайной величины Y.