5. МОДЕЛИРОВАНИЕ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Универсальным методом моделирования непрерывных случайных величин является метод исключения. При моделировании случайной величины Х с плотностью распределения вероятности в интервале от a до b используется следующий алгоритм:

1. Получение от датчика случайных чисел с равномерной плотностью распределения вероятности в интервале от 0 до 1 двух независимых значений случайных величин: и .
2. Расчет = а + (b - а) , = f_max,  где   f_max - максимальное значение  f(х).
3. Если , то представляет моделируемое значение случайной величины. Если данное неравенство не выполняется, то возвращаемся к пункту 1.

Программа 3 ( исходный файл lect1_3.cpp , выполняемый файл lect1_3.exe )

Разработать функцию, формирующую (моделирующую) значения случайной величины с плотностью распределения вероятности на интервале . Эта зависимость показана на следующем рисунке.

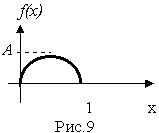
Вычислим А : 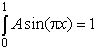- вероятность достоверного события равна 1.
Далее, вычисляя интеграл, получаем: .
Из чего следует А=.

#define N 500
#define M 30000L
#include 
#include 
#include "model.h"
float sl_vel(void);
      float f[N] ;
void main(void)
{  long i ;     int  n;
   float x  ;
         for(i = 0 ; i < M ; i++)
       {	 x = sl_vel();
	 n =  x * N ;
	 f[n] = f[n] + 1./M * N ;
       }
	 Init_graph();
	 graf_1("plotnost", f, 0, N-1);
      Close_graph();
}
float sl_vel(void)
{
  float   , ,  ,  ;
  for(; ;)
  {  = random(30000)/30000.;
      = random(30000)/30000.;
	     =   ;
	    = PI /2 *  ;
	    if ( <= ( PI/2 * sin (PI*  ))) break;
   } return  ;
 }

Программа 4 ( исходный файл lect1_4.cpp, выполняемый файл lect1_4.exe )

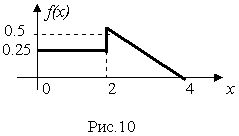
Далее приведена программа моделирования случайной величины с плотностью распределения вероятности (рис.10):

#define N 500 #define M 30000L #include #include "model.h" float sl_vel(void); float f[N]; void main(void) { long i; int n; float x, a = 0, b = 4, d; d = (b - a)/ N ; for(i = 0; i < M ; i++) { x = sl_vel(); n = (x - а) /(b-a) * N ; f[n]=f[n]+1. /M */d; } Init_graph(); graf_1(" plotnost ", f, 0, N-1); Close_graph(); } float sl_vel(void) { float a=0, b=4, , , , , z; for(;;) { = random(30000)/30000.; = random(30000)/30000.; = a + ( b-a) * ; = 0.5 * ; if( <= 2.0) z = 0.25 ; else z = 1 - 0.25 * ; if ( <= z ) break; } return ; }