6. МОДЕЛИРОВАНИЕ ГАУССОВСКИХ СЛУЧАЙНЫХ ВЕЛИЧИН

В технике и природе наиболее распространенное распределение случайных чисел - гауссовское или нормальное. Его плотность вероятности записывается следующим образом:

Здесь - дисперсия случайной величины, а M{X} - математическое ожидание случайной величины X.

Распространенный алгоритм моделирования таких величин основан на центральной предельной теореме, согласно которой, закон плотности распределения вероятности суммы независимых случайных величин стремится к нормальному при увеличении числа независимых случайных величин.

Алгоритм. Берется датчик случайной величины, которая имеет равномерную плотность распределения вероятности в интервале от 0 до 1. При этом математическое ожидание случайной величины равно 0.5, а ее дисперсия равна 1/12. Если просуммировать порядка 8-10 независимых реализаций СВ, то результатом суммирования будет случайная величина с плотностью распределения вероятности, очень близкой к гауссовскому закону. Таким образом, алгоритм получения гауссовской СВ выглядит следующим образом:

,

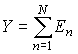где - случайные величины с равномерной плотностью распределения вероятности в интервале от 0 до 1. Математическое ожидание и дисперсия величины Y соответственно равны M{Y}=N/2, D=N/12. Далее приведена программа формирования нормальной случайной величины с нулевым математическим ожиданием и единичной дисперсией. Для получения одной реализации такой случайной величины суммируются 10 независимых случайных величин с равномерной плотностью распределения вероятности в интервале от 0 до 1.

Программа 5 ( исходный файл lect1_5.cpp , выполняемый файл lect1_5.exe )

#define N 500
#define M 50000L
#include 
#include 
#include "model.h"

float gauss_test(void);
float   f[N] ;

void main(void)
{  long m;
    int n; float x, a = -5, b = 5, d;
	            d = (b-a)/N;
       for(m =0 ; m < M; m++)
       { x = gauss_test();
n = (x - a) / (b - a) * N;
	f[n] = f[n] +1;
       }
       for (n=0; n < N ; n++)
	 f[n] = f[n] / (M * d);

    Init_graph();
    graf_1(" plotnoct  gauss", f, 0, N-1);
    Close_graph();
  }

float gauss_test (void)
{
 float x;
 int i, N_cycle =10;
 x = 0.0;
   for(i = 0 ; i < N_cycle; i++)
    x = x + random(30000)/30000.0;
    x = x -0.5* N_cycle;
    x = x/sqrt (N_cycle /12.);
    return x ;
 }