| Так, например, на рис.1, а: | e1(t)= e(mT) | при |
| на рис.1, б: | e2(t)=[e((m+1)T)+e(mT)]/2 | при |
| на рис.1, в: | e2(t)=e(mT)+[e((m+1)T)-e(mT)]y/T | при |
Большинство реальных процессов характеризуется непрерывным временем и непрерывными значениями самих процессов. В этом случае для моделирования на вычислительной технике непрерывную функцию времени необходимо преобразовать в дискретную, что называется аппроксимацией непрерывной функции. Наиболее известные виды аппроксимации показаны на рис.1, а, б, в.
| Так, например, на рис.1, а: | e1(t)= e(mT) | при |
| на рис.1, б: | e2(t)=[e((m+1)T)+e(mT)]/2 | при |
| на рис.1, в: | e2(t)=e(mT)+[e((m+1)T)-e(mT)]y/T | при |
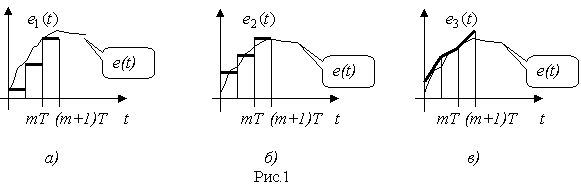
Таким образом, исходное непрерывное воздействие на систему заменяется другим (приближенным). Очевидно, что чем меньше шаг дискретизации и точнее аппроксимация, тем ближе реальный процесс на выходе системы и моделируемый процесс. Наиболее интересный вопрос здесь связан с выбором шага дискретизации. Известно, что полностью характеризовать линейную систему можно с помощью импульсной характеристики k(t), которая является реакцией системы на дельта-функцию ![]() Другой способ описания системы - это частотная характеристика, которая представляет собой зависимость комплексной амплитуды отклика системы от частоты гармонического входного воздействия.
Другой способ описания системы - это частотная характеристика, которая представляет собой зависимость комплексной амплитуды отклика системы от частоты гармонического входного воздействия.
Рассмотрим ситуацию, когда входным воздействием является случайный процесс. Это связано с тем, что случайный процесс наиболее полно характеризует различные возможные воздействия, в том числе и разнообразные детерминированные.
Здесь возможны две ситуации:
| 1) | полоса частот входного процесса (ширина спектральной плотности мощности случайного процесса) намного шире полосы частот пропускания системы; |
| 2) | полоса частот входного процесса (ширина спектральной плотности мощности случайного процесса) соизмерима с полосой пропускания частот системы. |
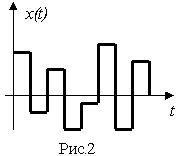
Для аналитического исследования систем, относящихся к первому пункту, широко используется модель под названием белый шум. В этом случае случайный процесс имеет равномерную спектральную плотность мощности на всем частотном интервале ![]() . Для цифрового моделирования существует другая модель - дискретный белый шум. Дадим более точное определение дискретного белого шума: это последовательность прямоугольных импульсов, при этом амплитуда каждого импульса представляет случайное число с нулевым математическим ожиданием. На рис. 2 показана реализация такой модели.
. Для цифрового моделирования существует другая модель - дискретный белый шум. Дадим более точное определение дискретного белого шума: это последовательность прямоугольных импульсов, при этом амплитуда каждого импульса представляет случайное число с нулевым математическим ожиданием. На рис. 2 показана реализация такой модели.
 |
Спектральная плотность мощности такой модели аналитически записывается следующим образом: (1) |
Рассмотрим процесс перехода от модели белого шума к дискретному белому шуму.
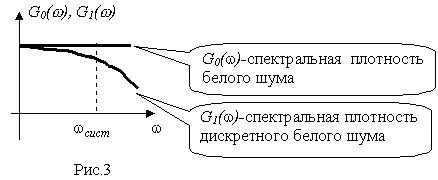
Любая система имеет ту или иную граничную частоту ![]() , которая ограничивает частоты проходящие на выход системы. Очевидно, что для того, чтобы на интервале частот от 0 до
, которая ограничивает частоты проходящие на выход системы. Очевидно, что для того, чтобы на интервале частот от 0 до ![]() можно было заменить (рис.3) равномерную спектральную плотность функцией
можно было заменить (рис.3) равномерную спектральную плотность функцией ![]() она должна незначительно отличаться от
она должна незначительно отличаться от ![]() на интервале от 0 до
на интервале от 0 до ![]() :
:
Как правило, приемлемая точность соответствует ![]() для
для ![]() . Разлагая функцию (1) в ряд, получим условие для выбора шага дискретизации:
. Разлагая функцию (1) в ряд, получим условие для выбора шага дискретизации:
| (2) |
Далее основная проблема сводится к тому, чтобы определить ![]() . Для этого рекомендуется решить [3] следующее уравнение относительно
. Для этого рекомендуется решить [3] следующее уравнение относительно ![]() при b = 0.95 - 0.99:
при b = 0.95 - 0.99:
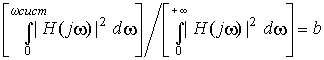 .
.Здесь ![]() - частотная характеристика.
- частотная характеристика.
Реально для большинства (даже несложных систем) нелегко выполнить формальные вычисления для получения ![]() и, в дальнейшем для получения шага дискретизации Т. Поэтому рекомендуется приблизительно определить
и, в дальнейшем для получения шага дискретизации Т. Поэтому рекомендуется приблизительно определить ![]() - максимальную частоту пропускания системы, исходя из частотной характеристики системы, и выбрать приблизительно шаг дискретизации, исходя из условия
- максимальную частоту пропускания системы, исходя из частотной характеристики системы, и выбрать приблизительно шаг дискретизации, исходя из условия
| (3) |
Рассмотрим теперь выбор шага дискретизации при моделировании коррелированных случайных процессов (а именно, вторая ситуация). Как и ранее в качестве входного воздействия рассмотрим случайный процесс. Аппроксимация (см. рис.1) приводит к искажению входного процесса и, следовательно, выходного. За меру качества дискретной модели примем величину [3]
Здесь ![]() - дисперсия случайного процесса на выходе системы при условии непрерывного воздействия на входе;
- дисперсия случайного процесса на выходе системы при условии непрерывного воздействия на входе; ![]() - дисперсия случайного процесса, при условии, что входным воздействием является разность между истинным непрерывным входным случайным процессом и аппроксимирующей функцией.
- дисперсия случайного процесса, при условии, что входным воздействием является разность между истинным непрерывным входным случайным процессом и аппроксимирующей функцией.
Условие для выбора шага дискретизации [3]
| (4) |
где
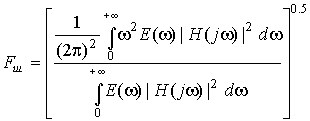
Здесь ![]() - спектральная плотность мощности входного процесса. Практически вычислить
- спектральная плотность мощности входного процесса. Практически вычислить ![]() достаточно сложно, и здесь также подходит условие (3).
достаточно сложно, и здесь также подходит условие (3).
Пример 1. На вход линейной системы с частотной характеристикой, показанной на рис.4, поступает случайный процесс - белый шум. Необходимо определить шаг дискретизации при действии белого шума на такую систему. Считаем параметр |
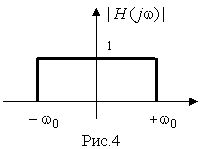 |
Пример 2. На вход линейной системы, описанной в примере 1, поступает случайный процесс с равномерной спектральной плотностью мощности в том же интервале частот. Определить шаг дискретизации при моделировании данной системы.
Считаем ![]() , и, вычисляя по формуле (4), получим
, и, вычисляя по формуле (4), получим ![]() .
.