В книге Устенко Анатолия Семеновича рассматриваются методические вопросы создания и применения математических моделей в процессе научных исследований. Формулируются основные понятия и принципы моделирования как метода научного познания. Определяются основные этапы разработки математических моделей сложных систем и процессов, методические подходы к выполнению начальных этапов моделирования: концептуального проектирования, формализации и алгоритмизации моделей.
Значительное внимание уделено изложению нового математического аппарата: теории обобщенных кодов подмножеств, многозначной математической и вероятностной логики, метода синтеза логических структур алгоритмов. Предлагается концепция объектно-классификационного моделирования сложных систем любой природы.
Книга предназначена для научных работников, преподавателей ВУЗ-ов, аспирантов и адъюнктов, занимающихся вопросами математического моделирования и алгоритмизации сложных систем и процессов.
ОТ АВТОРАI. МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ
1.1. Исходные понятия и определения.
1.2. Роль моделирования в процессе научного исследования
1.3. Понятие о подобии объектов
1.4. Математическое подобие объектов. Обзор способов определения коэффициентов подобия
1.5. Понятие о научном эксперименте, принцип максимального правдоподобия математических моделей
1.6. Понятие о методе максимального правдоподобия
1.7. Методика вычисления коэффициентов уравнения регрессии с помощью матричной алгебры
1.8. Моделирование объектов и систем, не допускающих активных экспериментов
1.9. Проблема оценки правдоподобия моделей не существующих (проектируемых) систем
II МАТЕМАТИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ И АЛГОРИТМИЗАЦИИ СЛОЖНЫХ СИСТЕМ
2.2. Представление множеств и подмножеств обобщенными кодами.
2.3. Исчисление обобщенных кодов подмножеств универсума
2.4. Элементы теории отношений. Общее понятие и свойства отношений
2.5. Понятие об исчислении высказываний
Метод дедуктивного логического вывода2.7. Методика индуктивного логического вывода
2.8. Представление высказываний и отношений обобщенными кодами
Логические функции2.9.1. Определения и формы представления логических функций
2.9.2. Формальные представления логических функций класса P
o2.9.3. Принципы минимизации кодовых форм представления логических функций
2.10. Вероятностные логические функции общего класса
2.10.1. Формальное представление вероятностных логических функций
2.10.2. Вычисление вероятностей значений вероятностных логических функций
2.11. Алгоритмы и алгоритмические процессы
2.11.1. Основные понятия и определения
2.11.2. Математические модели алгоритмических процессов
2.11.3. Пример синтеза структуры типового алгоритмического процесса
2.11.4. Показатели качества алгоритмов и алгоритмических процессов
2.11.4.1. Обобщенные и частные показатели2.11.4.2. Показатель сложности решаемой задачи X®
Y
III. МЕТОДЫ РАЗРАБОТКИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ФУНКЦИОНИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
3.1. Системный подход и математическое моделирование, как научная методология решения проблем
3.2. Концептуальное проектирование математических моделей
3.2.1. Общие методические положения
3.2.2. Проектирование математической модели для уточнения параметров орбиты космического аппарата
3.2.3. Проектирование модели для оценки надежности сложной информационно-вычислительной системы
IV. ОБЬЕКТНО-КЛАССИФИКАЦИОННОЕ МОДЕЛИРОВАНИЕ СЛОЖНЫХ СИСТЕМ
4.2. Определение понятия “объект”
4.3. Введение в формальное моделирование атрибутов объектов
4.4. Классификация объектов. Пространство идентификаторов объектов.
5. Состояние объекта. Пространство состояний объекта.4.6. Моделирование отношений между объектами и классами объектов
Классификационный подход к определению отношений4.6.3. Моделирование отношений между параметрами объектов
. Моделирование отношений между различными объектами
Разработка специального программного обеспечения АСУ войсками представляет собой реализацию математических методов, моделей и алгоритмов, применяемых для решения задач управления войсками с помощью современных информационных технологий. Поэтому обобщение и дальнейшее развитие методических основ моделирования и алгоритмизации сложных процессов является актуальной научно-исследовательской проблемой, решение которой обеспечивает необходимый теоретический уровень и качество создаваемого программного обеспечения.
В настоящей работе излагаются результаты исследований в этой области, выполненных автором в течение ряда лет. Работа состоит из четырех разделов. В первом разделе изложены теоретические основы математического моделирования процессов функционирования сложных систем. Даны определения исходных понятий, основанные на принципах теории отражения и теории подобия. В общем виде рассматривается методология математического моделирования сложных процессов.
Во втором разделе изложены результаты теоретического обобщения формальных математических систем (исчисления множеств, исчисления высказываний и логических функций). Изложены результаты разработанных автором теории исчисления обобщенных кодов подмножеств и теории многозначных логических функций общего класса. Изложены методы проектирования логических схем алгоритмов на основе предложенной автором типовой структуры алгоритма и новых методов анализа и синтеза многозначных логических функций.
Предложен подход к оценке сложности логических задач и алгоритмов, основанный на понятии энтропии принятия решения.
В третьем разделе на примерах излагается методика концептуального проектирования математических моделей процессов функционирования различных систем.
В четвертом разделе излагается предлагаемая автором концепция обьектно-классификационного моделирования сложных систем любой природы и делается попытка формализации этой концепции.
Продолжение исследований в данном направлении может оказаться весьма результативным, особенно при приложении вышеуказанных формальных методов к проектированию логических схем диалоговых систем, баз данных и при создании формальных методов объектного программирования.
Метод оценки сложности логических задач и алгоритмов может быть использован при оценке трудозатрат на проектирование и разработку СПО.
I. МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ
1.1. Исходные понятия и определения.
Научное исследование есть процесс познания определенной предметной области, объекта или явления с определенной целью.
Процесс исследования осуществляется субъектом и заключается в наблюдении свойств объектов и выполнении действий с целью выявления и оценки важных с точки зрения субъекта-исследователя закономерных отношений между показателями данных свойств.
Моделирование является одним из наиболее эффективных методов исследования. Оно заключается в построении и изучении специальных объектов (моделей), свойства которых подобны наиболее важным, с точки зрения исследователя, свойствам исследуемых объектов (оригиналов). В широком смысле моделирование представляет собой научную дисциплину, в которой изучаются методы построения и использования моделей для познания реального мира.
Всякая научная дисциплина, как правило, основывается на исходных понятиях и определениях, позволяющих однозначно понимать язык, применяемый для изложения этой дисциплины. Моделирование, как научная дисциплина, также содержит ряд специальных понятий, которые составляют начало методологических основ этой науки. (Концептуальная часть науки).
Философскую концепцию моделирования составляют теория отражения и теория познания, а формально-методическую основу моделирования составляют теория подобия, теория эксперимента, математическая статистика, математическая логика и научные дисциплины, изучающие те предметные области, которые подлежат исследованию методами моделирования.
В данном разделе рассмотрим основные положения науки о моделировании реально существующих объектов и объектов, подлежащих созданию в будущем. Моделирование этих объектов имеет общую философскую основу, но существенно отличается в части прикладных методов исследования.
Изучение методологических основ моделирования целесообразно начать с рассмотрения философских понятий теории отражения реальной действительности в сознании некоторого субъекта. Это должно обеспечить нам однозначное понимание положений излагаемых далее прикладных теорий. Приведем определения наиболее существенных для моделирования философских понятий. Некоторыми из них мы уже пользовались без определения.
Предметная область - это мысленно ограниченная область реальной действительности или область идеальных представлений, подлежащая описанию (моделированию) и исследованию. Предметная область состоит из объектов, различаемых по каким-либо признакам (свойствам) и находящихся в определенных отношениях между собой, или взаимодействующих каким-либо образом.
В нашем представлении объект - это все что мы различаем как нечто целое, реально существующее, или возникающее в нашем сознании и обладающее свойствами, значения которых позволяют нам однозначно распознавать это нечто. Объект, на котором сосредоточивается внимание субъекта с целью исследования, называется объектом исследования
.Объекты воспринимаются и различаются субъектами лишь постольку, поскольку они обладают характерными свойствами или способностями. "Свойство" и "способность" также являются весьма важными понятиями в рассуждениях человека.
Свойством называется характерная особенность объекта, которая может быть замечена и оценена субъектом, например, вес, цвет, длина, плотность и тому подобное. Для оценки исследуемого свойства объекта субъект устанавливает определенную меру называемую показателем свойства. Для каждого показателя определяется множество значений (уровней, или градаций меры свойства), которые присваиваются ему в результате оценивания свойства. Следовательно, свойство объекта является реальностью, а показатель - субъективной мерой этой реальности, если, конечно, речь идет о реальных объектах.
Показатели всеобщих свойств материальных объектов, таких как пространство и время называются основными показателями. Подавляющее большинство показателей других свойств выражаются через показатели этих основных свойств. Поэтому единицы измерения основных показателей служат основой для построения стандартной системы единиц измерения физических величин и называются основными единицами измерения.
Выражение показателя некоторого свойства через основные единицы измерения, принятые в определенной стандартной системе единиц (мер), называется размерностью данного показателя.
С точки зрения субъекта свойства делятся на внутренние (собственные) свойства объектов, показатели этих свойств называются параметрами, и внешние, представляющие собой свойства среды, связанные некоторыми отношениями с параметрами данного объекта. Показатели свойств внешней среды, влияющих на параметры исследуемого объекта, называются факторами
.Свойства объектов выявляются только при их взаимодействии, или при сопоставлении объектов друг с другом. Сопоставление (комбинация) значений показателей, наблюдаемых свойств определенных объектов называется отношением. Говорят, что отношение истинно, если оно подтверждается практическим экспериментом, или логическим выводом. Отношение считается ложным, если оно опровергается практической проверкой, или логическим выводом. Иначе отношение считается неопределенным. Понятия "истинно", "ложно", "неопределенно" являются логическими значениями любого отношения, результатами субъективной его оценки.
Отношение называется функциональным (функцией F), если оно представляет собой однозначное отображение множества X значений показателя некоторого свойства в множество Y значений показателя того же, или иного свойства. Формально это записывают как F:= X ® Y, или как F(X)=Y, или
F I X ? Y, где “? ” декартово произведение множеств.Взаимодействие объектов определяется по результатам изменения значений показателей наблюдаемых свойств этих объектов. Поэтому каждому действию, или взаимодействию, мы присваиваем определенный результат. Это может быть значение, или определенная комбинация значений, показателей свойств взаимодействующих объектов. Действия над значениями показателей свойств объектов, выполняемые по определенным правилам и приводящие к предполагаемому результату, называются операцией или процедурой
.Значения показателей свойств объектов обозначаются символами из некоторого заранее определенного множества А, называемого алфавитом
.Множество объектов, взаимосвязанных между собой определенными отношениями, и выполняющих определенную общую для них целевую функцию или имеющих общее предназначение, называется системой
.Система, состоящая из алфавита А, строго определенных множеств отношений (G), операций (Q) и предназначенная для символического описания объектов и систем определенного класса, называется формальной системой. Такие системы используются в качестве языков математического моделирования.
Способность, по нашему мнению, есть готовность объекта проявлять определенные свойства в определенных условиях. И наоборот, способность объекта вести себя определенным образом квалифицируется как его свойство. Например, забегая вперед, отметим, что одним из свойств сознания человека является способность применять ранее накопленные знания для решения возникающих логических проблем. Эта способность называется интеллектом
.Энергия является одним из свойств материи, в силу которого все материальные объекты совершают движение в пространстве и времени, находясь в энергетическом взаимодействии и пространственно-временном отношении.
Пространство и время также являются всеобщими свойствами материи. Многочисленные эксперименты подтверждают, что все материальные объекты существуют не иначе как в пространстве и во времени. Как известно, значения показателей пространства и времени входят в состав основных единиц измерения всех физических свойств объектов.
Так как все свойства объектов изменяются во времени, то любой набор значений показателей этих свойств относится к определенному значению показателя времени (к моменту времени). Это отношение называется состоянием объекта.
Значения показателей свойств меняются с течением времени. В результате этого происходит смена состояний объектов. Акт смены состояний объекта, отнесенный к определенному промежутку времени, называется событием, а последовательность взаимосвязанных событий, происходящих на некотором интервале времени, называется процессом
.Важным всеобщим свойством материи является способность материальных объектов сохранять вещественные и энергетические результаты (следы) взаимодействия материальных объектов. В философии эта способность называется отражением. Высшая форма отражения проявляется в биологических системах, как способность чувственного восприятия окружающей среды, сохранения результатов восприятия и использования их для управления своим поведением.
Часть материально-энергетической системы, предназначенная для восприятия и хранения результатов отражения, с целью воспроизведения и использования их в интересах системы в целом, называется памятью. Результаты отражения объектов внешнего мира и внутренних ощущений в памяти человека называются образами
.Как правило, чувственные органы человека воспринимают не полный образ наблюдаемого объекта, а только те его свойства, которые данный человек считает наиболее существенными по каким-то причинам. Человек способен присваивать образам символические имена из некоторого языка и связывать эти имена определенными логическими (мысленными) отношениями. Сформированная в памяти человека логическая система имен (идентификаторов образов) называется понятием
.С другой стороны, понятие можно определить и как некоторую языковую конструкцию, имеющую определенный смысл, т.е. образное содержание.
Система понятий и логических отношений между ними, отражающая какую-нибудь сторону реальной действительности, называется знаниями. Каждый субъект обладает памятью и механизмом целенаправленной манипуляции понятиями и знаниями. В целом эта система называется сознанием
.Процесс целенаправленной манипуляции знаниями в сознании субъекта называется мышлением
.Сознание субъекта присваивает каждому понятию, как и образу, символическое имя, определенное на языке, которым владеет данный субъект. Из имен понятий и образов формируется текст, представляющий собой знания субъекта о некоторой предметной области, закодированные на данном языке. Наглядная схема определений, связанных с понятием предметной области, представлена на рис. 1.1.
Рис. 1.1. Схема определения понятия "знания о предметной области".
Таким образом, основным элементом любого знания является понятие, представленное на определенном языке. Понятие в процессе приобретения знаний и в процессе мышления субъекта имеет три значения:
Выражения, предложения и фразы со своими значениями образуются при помощи грамматики языка, используемого субъектом для представления знаний.
Грамматика представляет собой систему правил, определяющих логические отношения между понятиями с учетом их семантических, синтаксических и символических значений.
Следовательно, приобретение знаний о предметной области есть процесс формирования в сознании субъекта понятий о существенных свойствах объектов предметной области и отношений между понятиями в виде текста, состоящего из выражений, предложений и фраз, обладающих соответствующими семантическими, синтаксическими, и символическими значениями.
Анализ данного процесса позволяет выяснить механизм мышления субъекта и факторы, влияющие на правдоподобие (достоверность) знаний субъекта о предметной области, а также найти способы построения правдоподобных моделей предметных областей.
Сущность процесса исследования заключается в отыскании достоверных ответов на поставленные вопросы. Общеизвестно, что какой вопрос, такой и ответ. Научные исследования предполагают отыскание ответов на корректно поставленные вопросы. В таких вопросах, как правило, требуется выбрать одно из возможных (альтернативных) решений некоторой проблемы (задачи) по определенным условиям.
Условие, по которому осуществляется выбор искомого решения, называется критерием. Как правило, критерий формулируется в виде некоторого отношения на множестве значений определенного показателя, который будем называть аргументом критерия.
Роль моделирования в процессе научного исследованияЦелью исследования обычно является определение значений параметров исследуемого объекта удовлетворяющих определенному критерию. Это означает, что в процессе исследования необходимо изменять значения параметров исследуемого объекта и таким образом измерять значения показателя, служащего аргументом критерия.
Процесс исследования заканчивается, когда исследователь находит совокупность значений параметров объекта, удовлетворяющую заданному критерию с заданной достоверностью. Проведение таких исследований называется экспериментом
.На практике такое экспериментирование с реальными объектами, как правило, обходится очень дорого, либо вообще не представляется возможным из-за нежелательных последствий эксперимента. Поэтому обычно в таких случаях для проведения научных экспериментов реальные объекты заменяются соответствующими им более простыми, безопасными и доступными объектами, свойства которых подобны свойствам исследуемых реальных объектов в определенной существенной части.
Объект, с целью изучения которого проводятся исследования, называется оригиналом, а объект, исследуемый вместо оригинала для изучения определенных свойств, называется моделью. В качестве моделей могут выбираться естественные объекты, обладающие свойствами, подобными соответствующим свойствам оригинала, или же создаваться специальные искусственные объекты с нужными свойствами.
Моделирование есть метод (или процесс) изучения свойств объектов-оригиналов посредством исследования соответствующих свойств их моделей.
Модели, представляющие собой материальные объекты, называются натурными или материальными.
При исследовании сложных систем, как правило, создать адекватную физическую модель не представляется возможным. В этих случаях ограничиваются созданием и исследованием математических описаний закономерных отношений между значениями параметров оригиналов. Такие описания называются математическими моделями.
Математическая модель - это образ исследуемого объекта, создаваемый в уме субъекта-исследователя с помощью определенных формальных (математических) систем с целью изучения (оценки) определенных свойств данного объекта.
Пусть некоторый объект Q обладает некоторым интересующим нас свойством C
0. Для получения математической модели, описывающей данное свойство необходимо:1. Определить показатель данного свойства (т.е. определить меру свойства в некоторой системе измерения).
2. Установить перечень свойств С
1,...,Сm,, с которыми свойство С0 связано некоторыми отношениями (это могут быть внутренние свойства объекта и свойства внешней среды, влияющие на объект).3. Описать в избранной форматной системе свойства внешней среды, как внешние факторы х
1,...,хn, влияющие на искомый показатель Y, внутренние свойства объекта, как параметры z1,...,zr, а неучтенные свойства отнести к группе неучитываемых факторов (w1,...,ws).4. Выяснить, если это возможно, закономерные отношения между Y и всеми учитываемыми факторами и параметрами, и составить математическое описание (модель).
В обобщенном виде схема такого описания (моделирования) показана на рис. 1.2.
Рис. 1.2. Моделирование, как субъективное отражение
объективной реальности.
Как показано на этом рисунке реальный объект характеризуется следующим функциональным отношением между показателями его свойств:
Однако в модели отображаются только те факторы и параметры оригинального объекта, которые имеют существенное значение для решения исследуемой проблемы. Кроме того, измерения существенных факторов и параметров практически всегда содержат ошибки, вызываемые неточностью измерительных приборов и незнанием некоторых факторов. В силу этого математическая модель является только приближенным описанием свойств изучаемого объекта. А математическую модель можно определить еще и как абстракцию изучаемой реальной сущности
.Модели обычно отличаются от оригиналов по природе своих внутренних параметров. Подобие заключается в адекватности реакции Y модели и оригинала на изменение внешних факторов x
1,...xn. Поэтому в общем случае математическая модель представляет собой функциюгде p
1,...,pm внутренние параметры модели, адекватные параметрам оригинала.В зависимости от применяемых методов математического описания изучаемых объектов (процессов) математические модели бывают аналитические, имитационные, логические, графические, автоматные и т.д.
Главным вопросом математического моделирования является вопрос о том, как точно составленная математическая модель отражает отношения между учитываемыми факторами, параметрами и показателем Y оцениваемого свойства реального объекта, т.е. на сколько точно уравнение (1.2) соответствует уравнению (1.1).
Иногда уравнение (1.2) может быть получено сразу в явном виде, например, в виде системы дифференциальных уравнений, или в виде иных явных математических соотношений.
В более сложных случаях вид уравнения (1.2) неизвестен и задача исследователя состоит, прежде всего, в том, чтобы найти это уравнение. При этом к числу варьируемых параметров х'
1,...,х'n, относят все учитываемые внешние факторы и параметры исследуемого объекта, а к числу искомых параметров относят внутренние параметры модели p1,...,pm, связывающие факторы х'1,...,х'n, с показателем Y' наиболее правдоподобным отношением. Решением этой проблемы занимается теория эксперимента. Суть этой теории состоит в том, чтобы, основываясь на выборочных измерениях значений параметров х'1,...,х'n, и показателя Y', найти параметры p1,...,pm, при которых функция (1.2) наиболее точно отражает реальную закономерность (1.1). Понятие о подобии объектовПодобие есть определенное отношение между значениями показателей свойств различных объектов, наблюдаемое и измеряемое исследователем в процессе познания. Под подобием понимается такое взаимно однозначное соответствие (отношение) между свойствами объектов, при котором существует функция или правило приведения значений показателей данных свойств одного объекта к значениям тех же показателей другого объекта.
Математические (формальные) описания подобных объектов допускают приведение их к тождественному виду.
Другими словами, подобие есть отношение взаимно однозначного соответствия между значениями показателей однородных свойств различных объектов. Однородными называются свойства, имеющие одинаковую размерность показателей.
Вообще говоря, объекты с различной физической природой, например механические и электрические процессы, могут иметь однородные свойства, например свойство изменения во времени определенных параметров.
Известно несколько видов подобия объектов
[3].1. В зависимости от полноты учета параметров различают:
абсолютное (теоретическое) подобие, которое предполагает пропорциональное соответствие значений всех параметров данных объектов,
т. е. pj(t) / rj(t) = mj(t), где j=1,n;
практическое подобие - определенное функциональное взаимно однозначное соответствие параметров и показателей определенного подмножества свойств, существенных для данного исследования;
практическое полное подобие - соответствие показателей и параметров выделенных свойств во времени и пространстве;
практически не полное подобие - соответствие параметров и выделенных свойств показателей только во времени, или только в пространстве;
практическое приближенное подобие - соответствие выделенных параметров и показателей с определенными допущениями и приближениями.
2. По адекватности природы объектов различают:
физическое подобие, предполагающее адекватность физической природы объектов (частными случаями физического подобия являются механическое, электрическое и химическое подобия объектов);
математическое подобие, предполагающее адекватность формального описания свойств объектов (частными случаями математического подобия являются статистическое, алгоритмическое, структурное и графическое подобие показателей свойств объектов).
Проблема определения подобных объектов состоит в выборе научно обоснованных критериев подобия и в разработке методов расчета этих критериев.
Изучению проблемы подобия объектов посвящена теория подобия. В рамках этой теории установлены три основных теоремы о подобии объектов, определяющие необходимые и достаточные условия подобия (критерии подобия).
Приведем краткое изложение содержания этих теорем
[3].
Теорема I. Подобные объекты имеют числено равные коэффициенты подобия (в теории подобия они называются критериями подобия), образованные из определенных сочетаний размерностей соответствующих параметров.
Чаще всего коэффициенты подобия представляют собой степенные комплексы размерностей, полученных из отношений (размерностей) параметров, учитываемых при описании объектов.
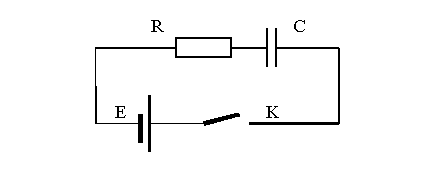
Например. Переходный процесс в электрическом контуре рис. 1.3.
может быть описан следующим дифференциальным уравнением:
duс /dt + uc - E = 0.
Рис. 1.3. Электрический контур с параметрами R, C, E, t, uс
.
Параметрами этого процесса являются: R, C, E, uс, t.. Из данного уравнения путем определенных преобразований получают следующие коэффициенты подобия:
p 1 = RC/ t= R1 C1 t-1 uc0 E0,
p 2 = E/uc = E1 uc-1 R0 C0 t0.
Коэффициенты подобия являются безразмерными величинами. Их значения одинаковы для любых наборов значений параметров электрического контура данного вида, т.е. для всех подобных электрических контуров с заданной схемой и номенклатурой параметров, взаимосвязанных приведенным выше дифференциальным уравнением.
Данная теорема носит имя Ньютона, или Ньютона-Бертрана.
Теорема II. Всякое уравнение физического процесса F(p
1,...,pn)= 0, записанное в определенной системе единиц измерений, может быть представлено в виде соответствующего уравнения F`(p 1, ... , p m) = 0 между коэффициентами подобия p 1, ... , p m, полученными из параметров p1 ,...,pn , задействованных в исходном уравнении F(p1, ...,pn--k)= 0.Для примера, показанного на pис.1.3., это уравнение имеет вид:
1+ p 1 - p 2 = 0.Данная теорема называется p-теоремой. Она говорит о том, что множество описаний подобных объектов можно привести к единому уравнению соответствующих коэффициентов подобия. Все подобные объекты имеют единый математический образ.
Теорема III. Необходимыми и достаточными условиями подобия объектов (оригинала и модели), описываемых однородными уравнениями F(P
1,...,Pm)= 0 и F(R1, ...,Rm)= 0 , являются:Известны также дополнительные условия подобия для сложных объектов [
3]. Смысл этих дополнительных условий в следующем. Два сложных объекта подобны, если подобны все соответствующие элементы этих объектов и подобны функции (или отношения) связывающие данные элементы.По мере развития науки о моделировании, подобие приобретает все более широкое содержание. Возникли особые виды подобия:
квазиподобие, основанное на использовании переменных масштабных коэффициентов;
эквивалентное подобие, основанное на сравнении эквивалентных в том или ином смысле описаний, например на взаимно однозначном соответствии функций на некотором интервале;
алгоритмическое подобие, основанное на сопоставлении выполняемых алгоритмов;
кибернетическое подобие, основанное на подобии функций управления, реализуемых различными объектами.
Далее мы будем говорить только о математическом подобии сложных процессов.
Математическое подобие объектов. Обзор способов определения коэффициентов подобияНапомним, что математическое подобие есть подобие математических выражений (описаний), характеризующих одинаковые свойства объектов, необязательно адекватных по своей материальной природе.
Например, процесс изменения напряжения u
c в контуре электрической цепи, состоящей из активного сопротивления R, емкости C, индуктивности L, источника напряжения E и выключателя K, описывается такими же дифференциальными уравнениями, как и процесс колебания груза, подвешенного на пружине, под воздействием силы тяжести и некоторого импульса. Однако, параметры уравнений, описывающих эти два процесса, будут иметь различную размерность. Но коэффициенты подобия безразмерны и будут иметь одинаковые численные значения. Это математическое подобие позволяет изучать механические колебания на электрических моделях и наоборот.Известны и другие примеры формального математического подобия объектов, имеющих различный физический или семантический смысл.
Например, формулы вычисления вероятностей сложных событий по заданным значениям вероятностей простых событий, входящих в их состав, имеют формальное подобие формулам вычисления истинности сложных высказываний по значениям истинности составляющих их простых высказываний и т.д.
Таким образом, говоря о математическом подобии двух объектов, мы всегда имеем в виду подобие, вернее тождественность, математических описаний однородных свойств данных объектов.
В таких случаях доказательство адекватности оригинала и модели сводится к доказательству вышеизложенных теорем о подобии объектов.
Если исследуемый процесс может быть описан однородным дифференциальным уравнением вида:
![]()
или интегральным уравнением вида:
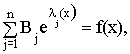
где х - параметр процесса, то коэффициенты подобия получают непосредственно из этих уравнений. Для этого данное уравнение приводят к безразмерному виду путем деления всех членов уравнения на один из этих членов и избавляются от знаков дифференцирования (интегрирования), считая, что отношения бесконечно малых величин равно отношению обычных значений параметров. Затем, члены уравнения преобразуют к виду
где j = 1,..., (n-1), C
j, a j,...,w j - безразмерные числа. Полученное при этом уравнение исследуемого процесса, представленное через коэффициенты подобия имеют вид:![]()
где n - число функций (членов) в исходном уравнении, m - число параметров исследуемого процесса.
В том случае, когда невозможно составить дифференциальное (интегральное) уравнение процесса, коэффициенты подобия можно определить из анализа любой функциональной зависимости, представляющей собой описание исследуемого процесса.
Пусть процесс описывается функцией F(p
1,...,pm) = 0, где - pj - размерные физические величины, характеризующие исследуемый процесс.Известно [
3], что любая такая функция может быть представлена в видеFp (p 1, p 2,..., p m-k) = 0,
где p
1,..., p m-k - коэффициенты подобия, k - число независимых параметров pj в множестве p1,...,pm.Если же математическое (функциональное) описание процесса в явном виде не известно, то коэффициенты подобия можно получить из словесного описания данного процесса методом анализа размерностей. Суть этого метода заключается в следующем.
1. Всякий процесс, объект или явление при моделировании или математическом описании представляется как уравнение или система уравнений.
2. Каждое уравнение отражает взаимосвязь параметров p
1,...,pm. (Параметр pi есть показатель определенного свойства Si).3. Каждый параметр имеет условную меру - единицу измерения [P
i]. Единицы измерения бывают основными {a,b,...,q} и производными. В общем случае [Pi] = f (a,b,...,q), обычногде
a, b,...,z - целые числа. Выражение (1.3) называется формулой размерности параметра (физической величины) или просто размерностью.Показатели свойств (параметры или физические величины) бывают однородными (характеризующими одно и то же свойство и имеющими одинаковую размерность), одноименными (имеющими одинаковую размерность, но характеризующими различные свойства, т.е. имеющими различный физический смысл), и безразмерными.
4. Группа параметров (показателей свойств) называется группой независимых параметров, если размерность ни одного из параметров не может быть образована из размерностей других параметров из той же группы. Например, группа (l,m,v) есть группа независимых параметров, так как размерность пути [l] определяется как [L], размерность массы [m] определяется как [M] и размерность скорости [v]
- как [V]=[L1T-1] и [V] не равно f([l],[m]).5. Признаком независимости параметров p
1,...,pm является существование хотя бы одного отличного от нуля определителя (D? 0) порядка k, образованного из элементов матрицы, составленной из показателей степеней при основных единицах измерения в формулах размерностей этих параметров.Пример. Даны параметры p
1,p2,p3 с размерностями [P1]=[Ll1Mm1Tt1], [P2]=[Ll2Mm2Tt2], [P3]=[Ll3Mm3Tt3]. Эти параметры независимы, если система уравнений:имеет единственное решение, а именно, когда
6. Для физического процесса, полностью характеризуемого m параметрами p
1,...,pm, среди которых k параметров p1,...,pk являются независимыми, существует m-k критериев подобия p 1, ... , p m-k. Число k равно рангу матрицы, образованной показателями степеней при основных единицах измерения параметров p1, ...., pm .7. В общем виде формулы для определения коэффициентов подобия имеют вид:
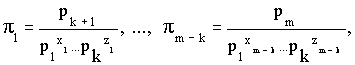
где x
i ,..., zi - показатели степеней, получаемые из системы уравнений:решением которой является выражение:
xi = D1 / D, ... , zi = Dk/ D,
где D - определитель системы (
1.4), D1,...,Dk - определители, составленные из D заменой соответствующего столбца 1,...,k столбцом свободных членов.Таким образом, коэффициенты подобия для параметров исследуемого процесса могут быть получены и при отсутствии уравнений, описывающих данный процесс в явном виде. Достаточно иметь набор всех параметров и их размерности.
Подробнее методику отыскания коэффициентов критерия подобия различных систем и явлений смотрите в
[3].1.5. Понятие о научном эксперименте, принцип максимального правдоподобия математических моделей
Выше было показано, что всякая математическая модель является только приближенным описанием некоторых свойств соответствующего реального объекта.
Единственным способом проверки степени соответствия модели и моделируемого объекта является научный эксперимент. Под экспериментом понимают целенаправленно организованный опыт, состоящий из воспроизведения и наблюдения исследуемого явления с необходимой точностью.
Математическое моделирование также представляет собой эксперимент, цель которого состоит в том, чтобы опытным путем, или путем логического вывода, найти неизвестные параметры
q1, ..., qm математической модели изучаемого процесса или объекта и построить соотношение Y* = F*( x1, ..., xn, z1, ..., zr, q1, ... qm) в явном виде так, чтобы в области варьирования факторов x1, ..., xn, z1, ..., zr функция Y* наилучшим образом приближалась бы к функции Y.Достижение этой цели основано на использовании принципа максимального правдоподобия математической модели (функции F
*) экспериментально полученным данным об исследуемом объекте.Принцип максимального правдоподобия основан на следующих известных положениях теории вероятностей.
1. Случайная величина Y полностью определяется (задается) функцией плотности распределения f(y,
h) ее значений, где h - параметр плотности распределения.2. Математическое ожидание случайной величины Y есть наиболее вероятное (правдоподобное) ее значение. Оно вычисляется по формуле:
E{y} соответствует максимальному значению этой функции.
Другими словами, наиболее вероятное значение E{y} случайной величины Y соответствует значению параметра h функции f(y, h), удовлетворяющему условию:
где
h - среднее значение величины y.Рис. 1.4. График функции плотности распределения вероятностей
Уравнение (1.5) называется уравнением правдоподобия , а решение h^ этого уравнения называется оценкой максимального правдоподобия случайной величины Y по параметру h. Оценка h^ параметра h осуществляется экспериментально по выборке значений y1, . . . , yn случайной величины Y из генеральной совокупности ее значений. При этом исходят из того, что вероятность получить выборку значений y1, ..., yn определяется по формуле:
где
в генеральной совокупности значений случайной величины Y.
Из данного выражения следует, что наибольшему значению вероятности (1.6) соответствует максимальное значение функции
вычисленное по параметру h.
Функция (1.7) называется функцией правдоподобия
h (среднего значения случайной величины Y) и записывается в виде l{h / y1, . . ., yn}. Часто применяется также логарифмическая функция правдоподобия, которая позволяет упростить вычисление оценки h^ параметра h по выборке y1, . . . , yn.1.6. Понятие о методе максимального правдоподобия
Метод максимального правдоподобия позволяет получать математические модели, характеризующие существенные свойства изучаемых процессов в виде функции правдоподобия (1.8) с оценкой параметра
h по результатам экспериментальных измерений показателя Y.Для этого необходимо:
1, . . . , yn значений случайной величины Y.* Априори установить характер закона распределения значений величины Y.
* Спланировать эксперимент и провести n опытов, в результате которых должна быть получена выборка y
* Определить функцию правдоподобия l{
h/ y1, . . . , yn } и оценить параметр h (в общем случае может быть множество параметров q1, ..., qm).* На основании полученной оценки
h^, или (q1^, . . . , qm^) сделать выводы относительно исследуемого показателя Y.Пример 1
. Предположим, что каждый из m стрелявших из пистолета произвел n выстрелов, стреляя по отдельной мишени. Затем наугад выбрана одна из мишеней. При этом в ней было обнаружено r попаданий. О каждом стрелке нам известно, что он способен попасть в мишень при одном выстреле с вероятностьюpj , jО {1, ...,m}.
Необходимо сделать правдоподобное предположение о том, кому из стрелявших вероятнее всего принадлежит выбранная мишень. Очевидно в качестве показателя Y, характеризующего процесс попадания в мишень одним стрелявшим с номером j при n выстрелах, может быть вероятность Pj(rn) попасть r раз в мишень для j-го стрелка при n выстрелах. Эта вероятность, как известно, распределена по закону Бернулли:
Параметр p^
j, максимизирующий вероятность P(r, n, pj), позволяет сделать вывод о том, что выбранная мишень с r пробоинами с наибольшей вероятностью принадлежит стрелявшему под номером j, который имеет способность (вероятность) pj попадать в мишень при одном выстреле наиболее близкую к оценке p^j. Для оценки p^j составляем функцию правдоподобияl{pj, r, n}=prj(1-pj)n-r. Данная функция достигает максимума при p^j = r/n [15]. Следовательно, наиболее вероятно, что выбранная мишень принадлежит стрелявшему под номером j, соответствующему оценке p^j=r/n.
Пример 2. Предположим, что задача состоит в том, чтобы оценить вес некоторого предмета посредством взвешивания его на n различных весах приблизительно одинаковой точности. В результате получается выборка у
1, y2, . . ., yn значений оцениваемого показателя Y, характеризующего вес данного предмета. Y является случайной величиной, распределенной по нормальному закону:где h - математическое ожидание величины Y, а s2 - дисперсия этой величины. Так как по определению s2 характеризует разброс значений yi относительно математического ожидания h, то величина s2 не влияет на положение максимума параметра h. Поэтому для упрощения вычислений можно положить s2 = 1. Тогда выражение (1.10) приобретает вид:
![]()
Отсюда формула правдоподобия параметра
h имеет вид:(При определении функции правдоподобия постоянные коэффициенты можно опустить) Функция (1.11) достигает максимума при таком значении h, для которого сумма
![]() принимает
минимальное значение. Этот факт был использован
для разработки широко известного метода оценки
параметров математической модели изучаемого
процесса, называемого “методом наименьших
квадратов”.
принимает
минимальное значение. Этот факт был использован
для разработки широко известного метода оценки
параметров математической модели изучаемого
процесса, называемого “методом наименьших
квадратов”.
При исследовании сложных систем показатель Y изучаемого свойства может быть функцией от многих факторов x1, ..., xn и представлять собой случайную функцию Y = f(x1, ..., xn, q1, ..., qm). Задача исследователя состоит в том, чтобы с помощью эксперимента определить такую функцию h(X, Q) c параметрами q1, ..., qm, которая с наибольшей вероятностью соответствует реальной функции Y. Согласно принципу максимального правдоподобия полагают, что функция h(X,Q) должна представлять собой множество значений {E(yi)}, где E(yi) - математическое ожидание случайной величины Y в точке Xi (Xi - набор значений факторов x1, ..., xn в точке i ).
Функция
h(X,Q) обычно представляется в виде линейного относительно параметров q1, ... qm полиномакоторый называется уравнением регрессии
случайной величины Y. В случае однофакторной функции Y ее уравнение регрессии может быть представлено в виде разложения в ряд Фурье:h ( x, Q) = q 0 1/2 + q 1 Sin (x) + q 2 Cos (x) + ... ,
или в виде разложение в ряд Тейлора:
h (x,Q ) = q 0 + q 1x + q 2x2 + ... .
В данном случае функция h ( х, Q ) называется линией регрессии. Когда функция U является многофакторной, применяется разложение в форме полинома (1.12) , где fi(x) представляет собой комбинацию из n по r факторов xiI {x1, ..., xn}. В этом случае число членов в разложении полинома определяется величиной
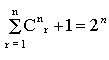 , а уравнение
регрессии, представленное таким полиномом имеет
следующий вид:
, а уравнение
регрессии, представленное таким полиномом имеет
следующий вид:
h ( C , Q ) = q 0(x01 x02 ... x0n) + q 1(x11 x02 ... x0n) + . . . + q 2n-1(x11 ... x1n). (1.13)
Поэтому проблема состоит еще и в том, как выбирать полином (1.12) так, чтобы трудоемкость вычислений была бы по возможности наименьшей. Эта проблема называется планированием эксперимента
. Для того чтобы полиномиальное представление функции h ( C , Q ) было хорошо обозримым и удобным для вычислений, введем следующие обозначения:XKj = (x1a 1,..., xna n)j,
где a
eI {0, 1}=Ae, e = 1,...,n, (a 1,...,a n)j= KjI {A1? ...? An}. Другими словами, Kj - есть двоичное число от (01, 02, ... , 0n) до (11,12, ..., 1n) . В силу данных обозначений XKj представляет (обозначает) вполне определенную комбинацию переменных x1, ..., xn, например, при Kj = (11, 02, ..., 0n) XKj= x1, при Kj = (11, 12, 03, ..., 0n) XKj = x1 x2 , и так далее. При этом полином (1.13) может быть записан в следующем виде: 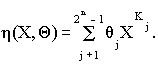 Данное
представление позволяет включать в полином
только некоторое ограниченное количество
членов, обеспечивающее заданную точность. Это
может быть использовано для построения
эффективных алгоритмов планирования
экспериментов и вычисления параметров q 0,...,q n.
Если случайная величина Y
распределена по нормальному
закону, то имеет место следующее уравнение:
Данное
представление позволяет включать в полином
только некоторое ограниченное количество
членов, обеспечивающее заданную точность. Это
может быть использовано для построения
эффективных алгоритмов планирования
экспериментов и вычисления параметров q 0,...,q n.
Если случайная величина Y
распределена по нормальному
закону, то имеет место следующее уравнение:
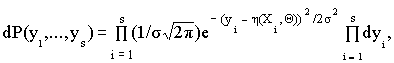 из которого
логарифмическая функция правдоподобия выборки y1,
..., ys случайной величины Y
получается в виде:
из которого
логарифмическая функция правдоподобия выборки y1,
..., ys случайной величины Y
получается в виде:
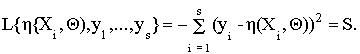
Чтобы найти значения функции h ( C i, Q ) , максимизирующие данную функцию правдоподобия в точках Xi , необходимо решить систему следующих дифференциальных уравнений:
¶ L{h ( C 1, Q ) , y1, ..., ys} / ¶ q j = 0, j = 1,...,m.
В общем случае эта система имеет следующий вид:
В результате решения данной системы линейных уравнений получают множество оценок q ^0, q ^1, ..., q ^m параметров q 0, q 1, ..., q m искомой функции h ( C i, Q ) . Для решения этой системы обычно применяют матричную алгебру. Система уравнений (1.14) может быть получена и другим способом. Данный способ основан на предположении, что каждое значение yi получается из опыта с некоторой погрешностью x i. При этом имеет место система уравнений
x i = yi - h ( C i, Q ) , i = 1,...,s.
Степень приближения функции h ( C
i, Q ) к экспериментальным даннымоценивается величиной дисперсии
Таким образом, приходят к соотношению
|S| = z , показывающему, что оценки параметров q j логарифмической функции правдоподобия S и дисперсии z имеют одинаковые значения в точке экстремума. Заметим, что данный способ не предполагает никаких ограничений на вид распределения случайной величины Y. Поэтому можно считать, что функция S (z ) годится для оценки параметров функции регрессии h ( C i,Q ) случайной величины Y при любом законе ее распределения.1.7. Методика вычисления коэффициентов уравнения регрессии с помощью матричной алгебры
Для решения системы дифференциальных уравнений, приведенной в предыдущем параграфе, с помощью матричной алгебры необходимо:
- представить полученные в результате опыта данные в следующем виде:
x i = yi - [q 0f0(xi) + q 1f1(xi) + ... + q mfm(xi)], i = 1, ... , s, (1.15)
где
s - число опытов в эксперименте;- ввести и определить конструктивную (структурную) матрицу:
- ввести и определить транспонированную матрицу параметров:
q' = (q 0, q 1, ..., q m);
- ввести и определить матрицу-столбец значений yi, i=1,...,s:
- представить систему (1.15) и функцию z в матричной форме:
(последнее уравнение получено с учетом того, что
- продифференцировать последнее выражение функции z по каждому параметру q i , в результате чего будет получена следующая система уравнений:
- решить данную систему, выполняя следующие действия:
Для получения решения q
^ необходимо, чтобы строки матрицы A' были линейно зависимы. Если при решении данной задачи использовать для представления уравнения регрессии формулу 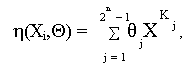 то вместо выражения fj(xi)
можно использовать выражение XKj
, при этом вычисления могут
быть существенно упрощены.
то вместо выражения fj(xi)
можно использовать выражение XKj
, при этом вычисления могут
быть существенно упрощены.
Пример. Пусть некоторый показатель исследуемого процесса представляет собой
случайную величину Y = F(x1, x2, x3). Тогда функция регрессии h ( C i,Q ) , представляющая собой математическое ожидание E{yi}, i = 1,...,s, можно представить в вид полиномаh ( C i,Q ) = q 0 + q 1x1 + q 2x2 + q 3x3 + q 4x1x2 + q 5x1x3 + q 6x2x3 + q 7x1x2x3 .
При этом заглавная строка структурной матрицы
A будет иметь следующий вид:x0 , x1, x2, x3, x1x2, x1x3 x2x3 x1x2x3,
а сама матрица
A, представляющая собой план проведения эксперимента, приобретает следующий вид: Таблица 1.1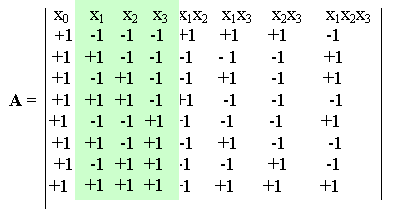
Данная таблица обладает следующими свойствами:
- добавлена фиктивная переменная x0 для приведения свободного коэффициента q 0 к общему виду;
- значения переменных xj, jI {0, 1, 2, 3} определены на множестве {-1, +1}, где -1 замещает наименьшее, а +1 - наибольшее значение переменной xj из области допустимых ее значений;
- комбинации значений независимых переменных x1, x2, x3 в данном случае представлены всеми возможными элементами декартового произведения {-1, +1} ? {-1, +1} ? {-1, +1}, которое называется полным или насыщенным планом эксперимента;
- значения таблицы, представляющие нелинейные члены полинома h (C i,Q ), получаются в результате перемножения значений переменных x1, x2, x3 в соответствующих столбцах таблицы;
- число строк s матрицы А соответствует наименьшему количеству опытов, необходимому для вычисления коэффициентов q (в данном примере s = 23, что соответствует количеству искомых параметров q j);
- матрица А должна обладать следующими свойствами:
симметричности
-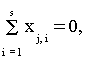 j = 1,2,...,7,
j = 1,2,...,7,
нормализованности
-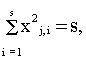
ортогональности
-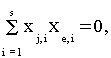 eО{1,...,7}, e№j, xj,i - функция из заглавной строки таблицы
1.1, представляющая собой комбинацию переменных x1,x2,x3.
При наличии перечисленных
свойств матрицы А коэффициенты q
j определяются по
формуле
eО{1,...,7}, e№j, xj,i - функция из заглавной строки таблицы
1.1, представляющая собой комбинацию переменных x1,x2,x3.
При наличии перечисленных
свойств матрицы А коэффициенты q
j определяются по
формуле 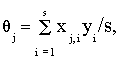 а дисперсия этих
параметров - по формуле s 2 {q j} = s 2 {yi} / s. Приведенная методика годится для
оценки параметров любой многофакторной функции h ( C i,Q ) .
Классическим примером применения метода
максимального правдоподобия является задача
определения (уточнения) параметров орбиты
космического аппарата [8] .
а дисперсия этих
параметров - по формуле s 2 {q j} = s 2 {yi} / s. Приведенная методика годится для
оценки параметров любой многофакторной функции h ( C i,Q ) .
Классическим примером применения метода
максимального правдоподобия является задача
определения (уточнения) параметров орбиты
космического аппарата [8] .
Примечание. Использование вычислительной процедуры, реализующей метод наименьших квадратов с целью получения оценок коэффициентов модели, которые удовлетворяли бы условиям несмещенности, состоятельности и эффективности, предполагает выполнение следующих условий
[9]:1.8. Моделирование объектов и систем, не допускающих активных экспериментов.* независимые переменные представляют собой неслучайный набор чисел таких, что их среднее значение и дисперсия конечны,
* случайные ошибки x
i имеют нулевую среднюю и конечную дисперсию
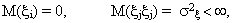
* между независимыми переменными отсутствует корреляция и автокорреляция,
* случайная ошибка не коррелированна с независимыми переменными,
* случайная ошибка подчинена нормальному закону распределения,
* зависимость между входными (независимыми) переменными и выходными (зависимыми) линейна.
Все, что было сказано ранее, относилось к моделям объектов и процессов, допускающих активное экспериментирование с факторами. Однако в природе существует много объектов и систем, не допускающих активный эксперимент. Проведение такого эксперимента либо не возможно из за отсутствия средств воздействия на объект (систему), либо может повредить объект или разрушить его.
В этом случае исследователь должен ограничиваться только пассивным наблюдением и измерением доступных ему свойств и параметров изучаемого объекта. При внимательном наблюдении за объектом всегда можно определить и измерить влияющие на объект природные факторы и зависящие от них показатели интересующих нас свойств объекта. При этом число измеряемых параметров может быть слишком большим. Проблема состоит в том, чтобы из всего множества измеряемых параметров отобрать необходимое минимально возможное количество наиболее существенных для данного исследования параметров.
Для решения данной проблемы используются методы математической статистики. К ним относятся методы корреляционного и факторного анализа.
Проблема оценки правдоподобия моделей не существующих (проектируемых) систем.Если система (процесс) вообще не существует
, а только предполагается (проектируется), то экспериментальное построение ее (его) математической модели в принципе не возможно. Однако априорная оценка свойств проектируемого процесса или системы необходима всегда. Создатель системы или процесса всегда должен предвидеть и оценивать последствия своей деятельности. За эти последствия он несет не только моральную, но и социальную ответственность.Математическое моделирование на ЭВМ позволяет решить эту проблему с достоверностью, которая определяется компетентностью самого создателя в своем деле и от эффективности применяемых им методов моделирования. Применение
“хороших” методов математического моделирования позволяет разработчикам сложных систем получать правдоподобные оценки проектируемых систем и прогнозировать возможные эффекты от применения этих систем.В нашем представлении хороший метод моделирования должен вытекать из общих законов теории познания и основываясь на законах логики, теории вероятностей, математической статистики и других строгих научных дисциплин, давать исследователю набор принципов, правил и алгоритмов, выполнение которых неизбежно приведет к построению модели, правдоподобной заданному процессу. При этом гарантируется вполне определенная степень правдоподобия.
главная об авторе содержание часть2 часть3 часть4 литература