II МАТЕМАТИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ И АЛГОРИТМИЗАЦИИ СЛОЖНЫХ СИСТЕМ
Элементы теории множествТеория множеств является формальной системой, позволяющей простым универсальным языком описывать сложные системы. Теория и практика математического моделирования сложных систем не может обойтись без этого эффективного математического аппарата. Поэтому прежде чем приступить к изложению основ теории моделирования напомним важные понятия теории множеств, которые будут использованы в дальнейшем.
Множество
- исходное понятие теории, обозначающее определенную совокупность некоторых объектов. Основными свойствами множества являются: дискретность, различимость элементов, целостность и идемпотентность({а, а,...,а} = {a}). Множества обозначаются буквами А, B, .. , Z и выражениями
{a1, ..., an}, где аi - символ элемента множества, i = 1,...,n. Основными отношениями абстрактных множеств являются:
Основными операциями над абстрактными множествами и подмножествами являются: проверка истинности заданного отношения,
Важное значение в построении формальной теории множеств имеют так называемые особые множества и подмножества
. К ним относятся:
В алгебре множеств ( точнее подмножеств универсума) понятия пустое множество и универсум играют роль аналогичную той, которую играют понятия нуль и единица в арифметике. Свойства перечисленных отношений и операций над множествами определяются системой аксиом, образующих абстрактную алгебру множеств. Аксиомы абстрактной алгебры множеств приведены в таблице 2.1.
Таблица 2.1. Основные свойства операций над множествами
Отметим, что данная алгебра абстрактных множеств не связана с какими-либо методами выполнения вышеупомянутых операций и проверки истинности отношений между множествами. Поэтому при работе с конкретными множествами указанные операции в общем случае выполняются посредством полного перебора элементов заданных множеств, а сами множества задаются в виде списков имен принадлежащих им элементов. Проблема компактного представления множеств и перебор их элементов является одной из основных проблем математического моделирования сложных систем. Для ее решения применительно к конечным перечислимым множествам предложена теория исчисления обобщенных кодов подмножеств [14].
Представление множеств и подмножеств обобщенными кодами.
Пусть U - множество универсум, содержащее в себе все элементы с определенными свойствами, например множество всех людей, множество всех космических аппаратов, множество всех вещей, находящихся в вашей комнате и так далее. Для описания свойств всех элементов универсума вводится база переменных X
1, X2, ..., Xn, характеризующих показатели соответствующих свойств Si элементов из U и принимающих значения из множеств Ai = {a0, a1, ..., as}i, i = 1,...,n. При этих обозначениях элемент из U представляется кортежем (кодом)kj = (ае1, аg2, ..., аsn)О(A1ґ A2ґ ... ґ An). Пусть символ a i обозначает любое, в том числе и пустое, подмножество из Аi, тогда кортеж Кj= (a 1, a 2, ..., a n) будем называть обобщенным кодом подмножества
Mj = (a 1ґ a 2ґ ...ґa n)Н(A1ґ A2ґ ... ґ An) = U. Другими словами, Kj есть код подмножества Mj из универсума U. Обобщенный код Kj, в котором все компоненты a 1,...,a n представляют собой конкретные значения ае1,..., аsn переменных X1,...,Xn, называется элементарным кодом, то есть - кодом отдельного элемента из U.
Пример. Пусть U есть множество людей, обладающих следующими свойствами: X
1 - имя из множества {петр, ольга, иван, фома}=A1,X2 - пол из {мужчина, женщина}=A2,
X3 - год рождения из {1950, ..., 1996}=A3,
X4 - образование из {начальное, среднее, высшее}=A4. Тогда конкретные люди из множества U обозначаются элементарными кодами, например К1=(иван, мужчина, 1960, высшее), а подмножество M2 из U всех мужчин, не имеющих высшего образования, обозначается обобщенным кодом
К2=(- 1, мужчина,щ высшее, - ), где
знак - 1 означает, что
переменная Х1 может принимать любое
значение из множества А1. Весьма важную
роль в теории множеств и в других формальных
системах играют так называемые особые
подмножества, к которым относятся:
одноэлементное множество {a}, пустое множество 
,
собственно множество А в целом, дополнение
элемента {a} к множеству А, перечисление элементов
({ae}, ..., {ag}) из А, перечисление
дополнений и дополнение перечисления. Для
построения обобщенных кодов в теории исчисления
обобщенных кодов [14] используются
специальные символы особых подмножеств базовых
множеств Ai. Вот эти символы: aei » {ae}iОAi,
` aei » (Ai
\ {ae}i) или щ aei »
(Ai \ {ae}i), - i » Ai,
q i » ,
(ае, ..., а
s)i » {{ae}, ..., {as}}iН Ai, щ (ае, ..., аs) » Ai \ {{ae}, ..., {as}}iи (
щ ае, ..., щ аs). Здесь символ “» ” используется в качестве символа метаязыка, обозначающего эквивалентность выражений. В формальных выражениях исчисления обобщенных кодов символ a i обозначает переменную с множеством значений{aei,` aei, - i, q i, (ае,...,аs),
щ (ае, ..., аs), (` ае, ...,` аs) }. Поэтому формула Кj=(a 1,...a i,...,a n) означает, что в конкретных обобщенных кодах символы a i замещаются соответствующими символами особых подмножеств из множеств Аi. Позиции переменных a i в обобщенном коде Кj называются разрядами обобщенного кода. Разряды различных обобщенных кодов, относящиеся к одной и той же переменной Хi, называются одноименными. Представление подмножеств универсума U обобщенными кодами позволяет выполнять над ними все теоретико-множественные операции по формальным правилам, посредством определенных действий над обобщенными кодами, подобно тому, как выполняются операции над числами, представленными цифровыми кодами. Термин “обобщенный код” заимствован из работ профессора Л. Т. Мавренкова (ВИА им.Ф.Э.Дзержинского), где он использовался для обозначения интервалов двоичных чисел. Исчисление обобщенных кодов подмножеств универсумаИсчислением обобщенных кодов подмножеств M
jН U называется формальная система, в которой определены:В дальнейшем, для краткости, вместо слов: “отношение (операция) над подмножествами Mj и Mk,представленными обобщенными кодами Kj и Kk”, будем говорить: “отношение (операция) над кодами Kj и Kk”, имея в виду, что речь идет о действиях над соответствующими подмножествами элементарных кодов, представленными в обобщенных кодах Kj и Kk.
Пусть K
j= (a 1,..., a i, ..., a n)j и Kk= (a 1,..., a i, ..., a n)k,где a
ij, a ikО {- i, aei, ` aei, q i, (аe,...,аs), щ (аe, ..., аs), (` аe, ...,` аs) },iО{1,...,n}, j,kО{1,...,m}, и пусть предполагается, что отношения между символами особых подмножеств указывают на те же отношения между соответствующими этим символам подмножествами элементов aeiОAi. Тогда для определения истинности отношений между подмножествами MjНU можно применять следующие правила:
Пример 1. Дана база переменных (X12 X23 X33) с базовыми множествами А1={0, 1}, A2={0, 1, 2}, A3={0, 1, 2} и даны обобщенные коды K1=(1, 0, -) и K2=(1, ` 2, -). Номера разрядов обобщенных кодов строго соответствуют номерам позиций базовых переменных Xi, поэтому индексы разрядов в обобщенных кода можно опускать. Согласно правилу 3 данные обобщенные коды находятся в отношении K1МK2, так как (02)1М(` 22)2, а также (11)1=(11)2 и (- 3)1=(- 3)2. Действительно по определению K1={(1, 0,1), (1, 0, 0)}
и K2={(1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 0, 0), (1, 0, 1), (1, 0, 2)}.
Легко заметить, что подмножество элементарных кодов, представленное обобщенным кодом K
1, целиком содержится в подмножестве элементарных кодов, представленных обобщенным кодом K2 (смотри коды, выделенные жирным шрифтом).Определение. Обобщенные коды называются ортогональными, если они представляют непересекающиеся подмножества элементарных кодов. Отношение ортогональности обобщенных кодов будем обозначать символом ^ . Для проверки истинности отношения ортогональности обобщенных кодов установлено следующее правило: Kj ^ Kk (читается: Kj и Kk ортогональны), если хотя бы в одном одноименном разряде данных кодов имеется отношение a ij З a ik=q i, т. е. подмножества значений, представленные переменными a ij и a ik не пересекаются.
Пример 2. Коды (-
, ` 1, 2)1 и (- , 1, 2)2 ортогональны, так как подмножества {0, 2}21 и {1}22, представленные соответственно символами ` 1 и 1, не пересекаются.Определение
. Операция “@” над обобщенными кодами Kj и Kk, соответственно представляющими собой подмножества Mj и Mk из U, есть последовательность действий, приводящих к получению кода Kr или объединения кодов Kr,...,Kt, представляющих подмножество M*НU такое, что M* = Mj@Mk. Формальная запись операции над обобщенными кодами имеет вид Kj@Kk = {Kr,...,Kt,}. Для выполнения операций над обобщенными кодами подмножеств MНU были установлены следующие формальные правила. , если хотя бы в
одном разряде имеет место соотношение a
ijЗa ik=q
ir.
Пример 3. Для кодов K
1=(1,0,-) и K2=(1,`2,-) примера 1 в результате поразрядных операций находим: (11)1З(11)2=(11)3,(02)1З(`22)2=(02)3, (-3)1З(-3)2=(-3)3. Поэтому код пересечения будет следующим K3=(1,0,-). В данном случае K3=K1, так как K1МK2.
Пример 4. Двоичные обобщенные коды (-
,1,0,0)1, (-,1,0,1)2, (-,1,1,0)3, (-,1,1,1)4 можно объединить по третьему и четвертому разрядам, так как из значений этих разрядов можно составить декартово произведение А3ґА4={0,1}ґ{0,1}={(0,0),(0,1),(1,0),(1,1)}»(-3,-4), а остальные разряды имеют поразрядно одинаковые значения. Поэтому код данного объединения имеет вид (-,1,-,-).Пример 5. Коды K
1=(0,1,1), K2=(0,0,1), K3=(1,1,1), K4=(1,0,1) с базой A1={0,1}, A2={0,1,2}, A3={0,1,2} можно объединить в один обобщенный код Kr= (-,`2,1). Это следует из того, что {(0,0),(0,1),(1,0),(1,1)}=({0,1}ґ{0,1})=((-1)ґ(`22))=(-1,2), и при этом третьи разряды всех заданных кодов содержат одинаковые значения - “1”.Пример 6. Коды K
1=(0,`2,1), K2=(1,`2,1), K3=(0,2,1), K4=(1,2,1) с базой, указанной в предыдущем примере, можно объединить по двум первым разрядам. Это объединение выполняется так: (0,`2)1И(1,`2)2И(0,2)3И(1,2)4={0,1}ґ{0,1,2}=(-1)ґ(-2) = (-1, -2). В результате получим: K1ИK2ИK3ИK4=(-1, -2,1).Пример 7. Коды K
1=(1,2,1), K2=(1,2,0) с неизвестной базой можно объединить так K1ИK2=K3=(1,2,(1,0)). При этом, если затем окажется, что A3={0,1}, то можно преобразовать результат объединения к виду K3=(1,2,-), если A3={0,1,2}, то результат можно представить как K3=(1,2,`2).Из приведенных примеров видно, что объединение элементарных кодов в обобщенные открывает широкие возможности для экономного представления множеств конкретных объектов и анализа свойств этих множеств без полного перебора всех содержащихся в них элементов. Однако следует заметить, что одно и то же множество элементарных кодов может быть представлено различными обобщенными кодами. Поэтому важной проблемой теории исчисления обобщенных кодов является проблема поиска методов представления множеств элементарных кодов (подмножеств универсума U) объединением обобщенных кодов с минимальным числом обобщенных кодов или с минимальным количеством символов (a ei) значений переменных Xi в объединении обобщенных кодов. Ряд методов частичного решения данной проблемы известен в современной математической логике, где они используются для минимизации форм представления логических функций [4,14].
Определение
. Разностью Kj \ Kk называется объединение всех элементарных кодов из Kj, не принадлежащих пересечению KjЗKk, то есть R = Kj \ (KjЗKk). R= Kj, если KjЗKk=и R= K1ИK2И ... ИKs, если KjЗKk№и Kj№Kk.
, если Kj
= Kk;Пример 8. Найти разность R = (0,-
,`2,1)1 \ (0,0,0,-)2 обобщенных кодов с базой (X21,X32,X33,X24). Здесь верхний индекс указывает на значность переменной Xi, то есть на мощность базового множества Ai. Решение:
1) (-2)1 \ (02)2 = (` 02)r, поэтому K1r =(0,`0,`2,1),
2) (`23)1 \ (03)2 = (13)r, поэтому K2r =(0,-,1,1),
R = (0,`0,`2,1)И(0,-,1,1).
Читателю предлагается проверить, что R представляет собой все элементарные коды из кода (0,-
,`2,1)1, кроме кода (0,0,0,1), который является пересечением исходных обобщенных кодов K1 и K2. Операция вычитания обобщенных кодов является весьма полезной при решении многих практических задач с конкретными конечными множествами, представленными обобщенными кодами. Одной из таких задач является задача ортогонализации обобщенных кодов.
так как K
j ^ (Kk \ Kj) и Kk ^ (Kj \ Kk) по определению разности (Kj\Kk).
Пример 9. Представить объединение двух обобщенных кодов (0,`0,2,1)1И(0,-,1,1)2 из предыдущего примера объединением ортогональных кодов. Решение:
1) (0,`0,`2,1)1 \ (0,-,1,1)2 = (0,`0,0,1)3, поэтому
(0,`0,`2,1)1И (0,-,1,1)2= (0,-,1,1)2И(0,`0,0,1)3;
2) (0,-,1,1)2 \ (0,`0,`2,1)1= (0,0,1,1)4, поэтому
(0,`0,`2,1)1И(0,-,1,1)2=(0,`0,`2,1)1И(0,0,1,1)4.
Легко проверить, что полученные результаты представляют собой одно и тоже подмножество элементарных кодов, а именно:
Е={(0,0,1,1), (0,1,1,1), (0,2,1,1), (0,1,0,1) (0,2,0,1)}.
Элементы теории отношений. Общее понятие и свойства отношенийПример 10. Пусть дано K
1=(-,`2,0,0)1 с базой (X21, X32, X33, X24)1 и K2=(-,1,0)2 с базой (X25, X36, X37)2. Тогда K1ґ K2= (-1,`22,03,04,05,16,07). Свойства данной операции, в отличие от всех предыдущих, еще мало изучены и область ее применимости не исследована.
Подобно понятию “множество” понятие отношение является фундаментальным понятием математики. В математическом моделировании оно используется как исходное понятие для построения основных теоретических положений. Поэтому нам следует отдельно рассмотреть свойства отношений, методы их формализации и операции с отношениями.
Определяющими атрибутами любого отношения являются:
Всеобщими свойствами отношений являются:
Формальное определение понятия отношения обычно дается в терминах теории множеств. При этом, в общем случае, отношением называется подмножество R декартового произведения (A
1ґ A2ґ ...ґAn), где Ai - базовое множество значений некоторого свойства Xi.Отметим четыре важных частных случая:
Общий вид формулы любого отношения может быть следующим:
где аргументы представляют собой значения свойств объектов некоторого универсума, например БОЛЬШЕ(
x, y), ЛЮБИТЬ(Иван, Марья), СЛОЖИТЬ(10, 2, 4), И(дождь, ветер, звезд_ночной_полет). Заметим, что слова БОЛЬШЕ и И не являются глаголами, но при употреблении их в качестве имен отношений они соответственно имеют смысл (по умолчанию) “Быть больше” и “Одновременно иметь место”. В классической математике отношения R с однородной базой (AґA) называются бинарными [11]. Если (x,y)ОRН(AґA), то говорят, что элементы x и y находятся в бинарном отношении R. Формальная запись бинарных отношений имеет вид: (x,y)ОR, xRy, R(x,y) или x*y, где x и y любые элементы, взятые их множества А. Другими словами, x и y - переменные, принимающие значения из множества А, а R или * - имя отношения. В связи с тем, что по определению отношения R являются подмножествами некоторого универсума U, к ним применимы все известные нам теоретико-множественные операции. С другой стороны, все теоретико-множественные операции - суть отношения между объектами, определенными как множества. Кроме уже упоминавшихся теоретико-множественных операций для бинарных отношений дополнительно были установлены еще следующие операции: обращения R-1={ (x,y)| (y,x)ОR}, умножения R1° R2 = {(x,y)| ($ zОA) (xR1z и zR2y)} (последнее выражение читается: (x,y) есть результат умножения R1° R2, если существует элемент z из A такой, что xR1z и zR2y); а также отношение равенства D ={(a, a)| aОА}, представляющее собой диагональ множества (AґA), и отношение следствия R1ЮR2, означающее, что из истинности R1 всегда следует истинность R2. В общем случае отношения описывают на некотором формализованном языке определенные связи между естественными или абстрактными объектами. В то же время сами отношения по определению являются формализованными символьными объектами (формулами), обладающими вполне определенными логическими свойствами. Суть этих свойств для бинарных отношений показана в таблице 2.2, где x, y, z - символы переменных, характеризующих свойства каких-нибудь объектов из универсума U, * и · - символы переменных, обозначающих имена отношений, а Щ, Ъ, Ю, щ, є - формальные символы, соответствующие словам: И, ИЛИ, СЛЕДУЕТ, НЕ, ТОЖДЕСТВЕННО в их обычном смысле.Таблица 2.2. Основные свойства отношений
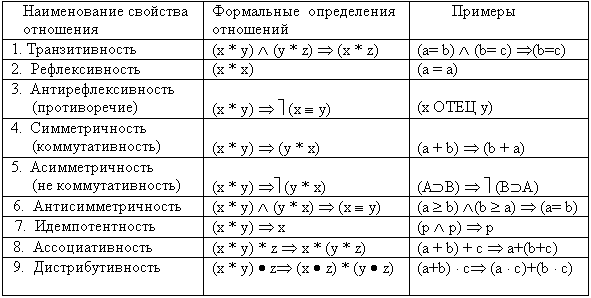
Изложенные определения и свойства отношений используются практически во всех разделах математики и математического моделирования, в частности, в ряде дедуктивных систем, моделирующих логику суждений. Одной из этих систем является исчисление высказываний, которое рассматривается в следующем параграфе.
Понятие об исчислении высказыванийПри моделировании проектов сложных систем единственным способом доказательства адекватности математической модели и будущей реальной системы является логический вывод правдоподобных суждений о свойствах будущей системы и об отношениях между ними. Формализация методов логического вывода суждений дается в теориях исчисления высказываний, логических функций и предикатов. Мы будем рассматривать высказывание как определенное отношение PНU, представленное на некотором формализованном или естественном языке. При этом будем полагать, что всякое высказывание Pi обладает свойством истинности (Xi) с областью значений Ei = {истинно, ложно}. Другими словами, Pi есть функциональное отношение, определенное в универсуме V= UґE, как функция fi(X1, ...,Xn), принимающая значения из множества истинности E. Значения “истинно”, “ложно” часто для краткости обозначают цифрами “1”, “0”. В этом случае их не следует воспринимать как какие-то количественные оценки, кроме как вероятности соответствующих логических значений “истинно”, “ложно”. Под исчислением высказываний понимают формальную систему операций и отношений, определенных в универсуме V. Всякая формальная система Ф определяется как четверка множеств (A, F, G, R), где A - алфавит символов языка данной системы, F - множество всех формальных выражений (формул), G - подмножество формул из F, называемых аксиомами, R - множество правил, служащих для вывода любой формулы из F из заданного множества аксиом. Пишут Ф = (A, F, G, R). В зависимости от смыслового определения множеств A, F, G, R возможны различные варианты исчисления высказываний. Известными частными случаями исчисления высказываний являются: булева алгебра, алгебра логики, логические функции и исчисление предикатов. Далее рассмотрим один из возможных обобщенных вариантов исчисления высказываний.
A = {p1,...,pn, 0, 1, ..., a, ...,z, E, истинно, ложно, ( , ) , щ , ® , » , є , Щ, Ъ , Ы , Ю }, где “A”, “=”, “{“, “}”, “,” - символы метаязыка, с помощью которого определяется исчисление, pi - элементарные высказывания о свойствах объектов из U, рассматриваемые как элементарные функции f(Xi) = a, aОE, 0,1,... - цифровые символы, которые используются как числа или как символы логических значений “ложно”, “истинно”, a, ..., z - буквы латинского алфавита, употребляемые в качестве значений свойств, о которых идет речь в высказываниях; E - множество {истинно, ложно}; щ , ® , » , є , Щ, Ъ , Ы , Ю - символы отношений между высказываниями и формулами, имеющие следующий смысл:
“pi” – любое высказывание, принимающее значение “истинно” или “ложно” при определенных условиях;
“щ pi“ - отрицание высказывания pi, представляет собой высказывание истинное, когда pi ложно, и ложное, когда pi истинно, другими словами, щ pi = (E \ { e }), если pi= e, eОE; такой же смысл имеет и запрись ` pi;
“pi ® pj” - импликация высказывания pj высказыванием pi, представляющая собой высказывание pk, ложное, когда pi истинно, а pj ложно, то есть pi ® pj= pk - (ложно) только если (pi, pj) = (истинно, ложно), где истинноО E и ложно ОE;
“pi » pj” - эквивалентность высказываний, представляющая собой истинное высказывание pk, тогда и только тогда, когда оба высказывания pi и pj имеют одинаковые значения истинности, то есть, когда (pi, pj) =(е, е), для всех (е,е)ОEґE;
“pi є pi” - тождество высказываний является всегда истинным высказыванием pk, независимо от значений входящих в него переменных pi, например щ щ pi;
“piЩ pj” - конъюнкция высказываний pi и pj есть отношение, соединяющее данные высказывания союзом “И”, высказывание pk = (piЩ pj) истинно только тогда, когда оба высказывания pi и pj истины;
“piЪ pj” - дизъюнкция высказываний pi и pj есть отношение, соединяющее данные высказывания союзом “ИЛИ”, высказывание pk = (piЪpj) ложно только тогда, когда оба высказывания pi и pj ложны;
“fiЫ fj” – равносильность есть отношение, указывающее на эквивалентность формул f, состоящих из высказываний и отношений между ними, fi равносильно fj, если они имеют одинаковые значения истинности на одинаковых наборах значений истинности высказываний и отношений, из которых они составлены;
“fiЮ fj” – следствие это высказывание, обозначающее тождественно истинную импликацию, говорят, что формула fj следует из формулы fi, если fj истинно на всех наборах значений переменных, на которых истинно fi.
1. Всякое высказывание, связанное со значением истинности из Е и обозначаемое символом pi, есть формула f.
2. Если выражение f - формула, то выражение
3. Если выражения fi и fj - формулы, то выражения (fi * fj), где *
О{® , » , є , Щ, Ъ , Ы , Ю } - тоже формулы.4. Других формул нет.
Аксиомы обычно определяются как бинарные функциональные отношения (элементарные функции f (p
i, pj)=e, eОE), из которых затем с помощью правил вывода составляются все остальные формулы данной системы. Истинность высказывания pk = fk (pi, pj) определяется в зависимости от истинности входящих в него высказываний pi, pj. Один из вариантов множества аксиом, которые мы будем использовать в дальнейшем, приведены в таблице 2.3, где для изображения формул применяются символы вышеперечисленного алгоритма и используются следующие обозначения: fk= fk (pi, pj), k=1, 2, ... 10, “1” » “истинно”, “0” » “ложно”.
4. Определение правил вывода.
Главной задачей формальной теории вывода является образование тождественно истинных формул (тавтологий) из заданного подмножества исходных тождественно истинных формул (исходных тавтологий).
Формула называется тавтологией, если она остается истинной при любых значениях входящих в нее высказываний. Например, формула f
1® f2 єщf1Ъ f2 является тавтологией, так как она истина при любых значениях ее компонентов f1 и f2, что легко проверить простой подстановкой этих значений в данную формулу.Вообще существует бесконечное множество тавтологий. Однако на практике задача вывода решается с использованием определенного ограниченного подмножества простых очевидных тавтологий и нескольких формальных правил вывода.
Простейшие тавтологии рассматриваемой версии исчисления высказываний образуются из аксиом, приведенных в таблице 2.3, с учетом свойств отношений, которые используются для их образования. Часть наиболее известных часто применяемых тавтологий представлена в таблице 2.4.
Таблица 2.4. Система основных тавтологий (законов) исчисления высказываний
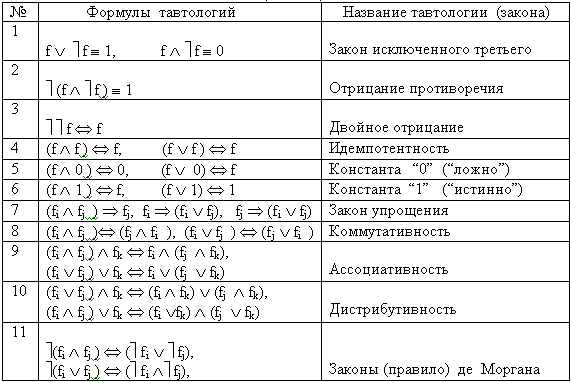
Для логического вывода обычно используют следующие два правила:
Формула
F (тавтология) называется выводимой в исчислении, если она может быть получена из конечного подмножества исходных формул (тавтологий) путем конечного числа операций по применению правил вывода. Вообще говоря, не все тождественно истинные формулы (тавтологии) могут быть выведены из произвольно взятого набора тавтологий. Однако, строго доказано, что в исчислении высказываний существуют такие конечные подмножества тавтологий (функционально полные системы аксиом исчисления), из которых может быть выведена любая тождественно истинная формула. Это означает, что задача об определении функционально полной системы аксиом исчисления высказываний является разрешимой. На практике обычно ищут и используют наиболее простые и удобные для практического применения функционально полные системы аксиом. Одной из таких систем является, например, система тавтологий представленная в таблице 2.4. Следует заметить, что процесс вывода формул связан с перебором множества возможных подстановок и с выбором вариантов, удовлетворяющих условиям тождества. Поэтому на практике задачи логического вывода связаны с большим объемом логических операций и часто из-за этого оказываются практически неразрешимыми. Метод дедуктивного логического выводаВ математической логике теория логического вывода предназначена в основном для формализации доказательства теорем
[5]. Доказательство теорем, как правило, ведется методом дедукции (от общего к частному), согласно которому истинное заключение выводится в результате конечного числа тождественных преобразований исходных формул в искомую заключительную формулу. Формальная схема этого метода преобразования имеет следующий вид:На практике этот метод логического вывода обычно используется для определения истинности конкретных отношений по заданным исходным отношениям (фактам), которые априори считаются истинными, и по определенным формулам (правилам вывода) следующего вида:
Вывод осуществляется по правилам подстановки заданных фактов в левую часть выражения 2.2 вместо содержащихся там символов переменных. Данная методика называется конкретизацией высказываний. В наших обозначениях конкретизация высказываний или отношений означает подстановку в его формулу конкретных значений
aeОA вместо входящих в нее предметных переменных X. Формальная постановка задачи конкретизации высказываний состоит в следующем. Дано:Требуется путем конкретизации заданных правил найти конкретные отношения
Fj, истинность которых по определению следует из истинности заданных исходных фактов и правил вывода.Пример. Пусть заданы следующие факты:
ЕСТЬ (Петр
, мужчина),РОДИТЕЛЬ (Петр
, Иван), и определено следующее правило вывода:ЕСТЬ(
X, мужчина) Щ РОДИТЕЛЬ(X, Y) ® ОТЕЦ(X, Y).Выполняя конкретизацию данного правила путем подстановки значений переменных
X и Y, которые они имеют в заданных фактах, получим конкретное отношение ОТЕЦ (Петр, Иван). Формализация и автоматизация данной методики вывода широко известна под именем системы ПРОЛОГ, включающей в себя специализированный язык логического программирования (Пролог) и реализующее его программное обеспечение [1,12]. Обратим внимание, что в классическом исчислении высказываний фактор времени рассматриваемых отношений в явном виде не указывается. Время действия отношения обычно определяется по форме глагола, употребляемого в качестве имени, или из контекста. Проблема формализованного представления (моделирования) высказываний и отношений с учетом времени и пространства сегодня еще не решена, несмотря на наличие значительного количества работ в этой области. Не менее интересной является и обратная задача, состоящая в том, чтобы по заданным конкретным фактам найти обобщенные формулы, представляющие собой правила вывода. По сути, это задача индуктивного вывода (вывода от частного к общему). Формальная постановка данной задачи состоит в следующем. Дано множество D факторов, отражающих определенные отношения в некоторой предметной области. Найти обобщенное правило, связывающее некоторые факты в тождественно истинные формулы с предметными переменными, характеризующими данную предметную область.Пример. Пусть заданы следующие факты:
ЕСТЬ (Петр
, мужчина),РОДИТЕЛЬ (Петр
, Иван),ОТЕЦ (Петр
, Иван),ЕСТЬ (Фома
, мужчина),ЕСТЬ (отец
, мужчина). Из этих фактов необходимо вывести формулуЕСТЬ(
X, мужчина) Щ РОДИТЕЛЬ(X, Y) ® ОТЕЦ(X,Y).В настоящее время формальная методика решения таких задач пока не существует, но она была бы полезной для решения многих практических и теоретических задач, связанных с поиском обобщенных выводов.
Методика индуктивного логического выводаДля построения методики индуктивного вывода мы разделим все возможные высказывания на три принципиально различных класса. К первому классу отнесем высказывания, определяющие свойства объектов. Формально эти высказывания представляют собой двухместные отношения вида
S(x, y), где S - имя отношения (свойства), xОX, yОY, X - переменная, определенная на множестве объектов, а Y - переменная, определенная на множестве значений свойства S, x и y - конкретные значения переменных X и Y соответственно.Пример. ЛЮБИТ (человек
, пиво), ЕСТЬ (Петр, мужчина).Ко второму классу высказываний отнесем высказывания, определяющие объекты. Формальные выражения для таких высказываний имеют следующий вид:
Q(S1ЩS2Щ...ЩSn), или Q(S1,S2,...,Sn), где Q - имя определяемого объекта, а Si - имя свойства, или его значения. В последнем случае наименование свойства должно быть определено заранее. Пример.ЧЕЛОВЕК (ИМЯ, РОСТ, ДАТА_РОЖДЕНИЯ, ОБРАЗОВАНИЕ),
ТРАНСПОРТНОЕ_СРЕДСТВО (автомобиль, СКОРОСТЬ_ ДВИЖЕНИЯ, ГРУЗОПОДЪЕМНОСТЬ).
Слово, состоящее из заглавных букв, означает переменную, вместо которой может быть подставлено значение из области ее определения. К третьему классу высказываний отнесем все высказывания, представляющие собой логические формулы, составленные из высказываний первого, второго и третьего класса.
Пример. ЕСТЬ(Петр
, человек) Щ ЛЮБИТ(человек, пиво) ® ЛЮБИТ(Петр, пиво).Заметим, что данная формула является истинной только тогда, когда отношение ЕСТЬ(Петр
, человек) обладает свойствами коммутативности и рефлексивности.
Первым условием индуктивного вывода является наличие
достаточного количества фактов, на базе
которых можно было бы сделать какие-то обобщения.
Вот пример простейшей базы данных (фактов), на
основании которой можно сделать некоторые
индуктивные выводы: Первым шагом
индуктивного вывода может быть объединение
объектов, обладающих одинаковыми значениями
одноименных свойств. При этом существует два
способа объединения объектов: дизъюнктивное
объединение с помощью связки ИЛИ и конъюнктивное
объединение с помощью связки И. Для получения
этих объединений в пределах заданной базы
достаточно выполнить, например, следующие
формальные преобразования:
По существу эти преобразования представляют собой вынесение за скобки значения “мужчина”, как свойства, которым обладают некоторые из перечисленных объектов (выражение 1), или все перечисленные объекты (выражение 2
). Пусть X1 - переменная, определенная на множестве A1={Петр, Иван, Фома}, тогда результат первого преобразования можно представить высказыванием СУЩЕСТВУЕТ(Х1, мужчина), а второго - КАЖДЫЙ(Х1, мужчина). Так мы приходим к известным классическим формам исчисления предикатов: $ xО A1 ЕСТЬ(x, мужчина), читается: существует x из A1 такой, что x есть мужчина, и " xО A1 ЕСТЬ(x, мужчина), читается: для всех x из A1 x есть мужчина. Так из конкретных фактов выводятся высказывания с предметными переменными, принимающими значения из определенных подмножеств. Отношение ЕСТЬ(X, Y) указывает, что аргумент X обладает свойством Y. По смыслу данного отношения объединять можно как объекты, обладающие одинаковыми свойствами, так и свойства, характеризующие одинаковые объекта. Следовательно, в заданной выше базе возможны и такие преобразования:ЕСТЬ(отец,
(мужчина Щ РОДИТЕЛЬ));Заметим, что в первом случае речь идет о свойствах одного и того же объекта, а во втором о свойствах различных объектов, имеющих одинаковое наименование. Это различие отражается соответственно символами “
Щ ” и “Ъ ”. Если предположить, что в любой формуле свойства S(x, y) первый аргумент всегда представляет собой имя (или имена) объектов, а второй аргумент представляет собой значение (или значения) свойства (или свойств) данного объекта, то будут справедливы следующие формальные соотношения:В процессе индуктивного вывода можно использовать также следующие правила обобщения отношений, содержащих переменные
X, Y и их значения x, y:Полезным является также условие эквивалентности отношений и высказываний. Оно состоит в том, что два высказывания (отношения), у которых все аргументы одинаковы, то есть имеют одинаковые наименования и значения, считаются эквивалентными. Другими словами, R1(X1,...,Xn)» R2(X1,...,Xn), если xi1=xi2 для всех i=1,...,n, xiО Xi. Xi - формула, представляющая собой свойство, объект или любое тождественно истинное высказывание. Пример.
ЕСТЬ(отец, мужчина)Щ РОДИТЕЛЬ(отец, X) ® отец ЕСТЬ (мужчина) Щ отец РОДИТЕЛЬ(X) ® отец (ЕСТЬ (мужчина) Щ РОДИТЕЛЬ(X));
ЕСТЬ(Петр, мужчина) Щ РОДИТЕЛЬ(Петр, Иван) ® Петр ЕСТЬ(мужчина) Щ Петр РОДИТЕЛЬ(Иван)® Петр( ЕСТЬ(мужчина) Щ РОДИТЕЛЬ(Иван));
РОДИТЕЛЬ(X) Щ РОДИТЕЛЬ(Иван)® РОДИТЕЛЬ(Иван);
РОДИТЕЛЬ(Иван) ® РОДИТЕЛЬ(X);
отец (ЕСТЬ(мужчина) Щ РОДИТЕЛЬ(Иван)) Щ Петр(ЕСТЬ(мужчина) Щ РОДИТЕЛЬ(Иван)) ® отец » Петр.
Таким образом, путем формальных преобразований можно доказывать эквивалентность различных наименований объектов, а также можно выводить абстрактные наименования свойств объектов и наименования самих объектов путем обобщения конкретных высказываний. Система тавтологий, пригодных для построения таких выводов, представлена в таблице 2.5. Таблица 2.5.
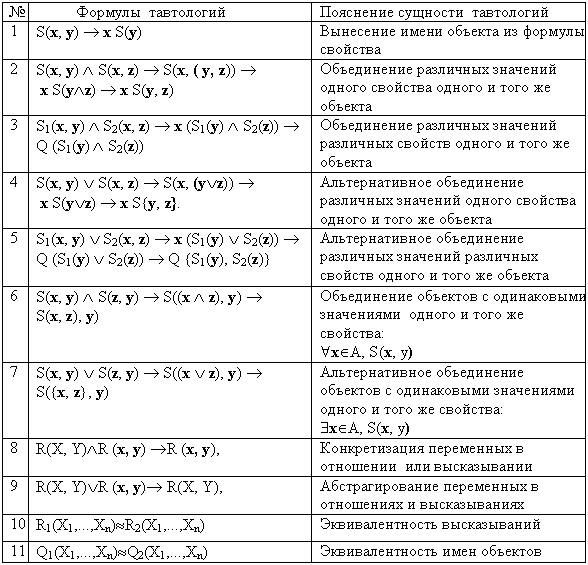
Данная таблица содержит подмножество тавтологий, позволяющих осуществлять некоторые индуктивные обобщения и выводы. При этом вопрос о функциональной полноте данного подмножества пока остается открытым. Это предмет дальнейших исследований. Я надеюсь, что плодотворные исследования в этой области позволят создать системы искусственного интеллекта, обладающие как дедуктивными, так и индуктивными способностями.
Представление высказываний и отношений обобщенными кодамиВ современной теории баз данных одна из возможных моделей базы данных представляется как отношение частичного порядка (Н) на множества типов объектов определенной предметной области [16]. Другими словами, база данных представляет собой описание системы подмножеств объектов, взаимосвязанных между собой отношением частичного порядка. Каждое подмножество включает в себя определенный тип объектов, который имеет собственное имя и характеризуется определенными свойствами, например подмножества ЧЕЛОВЕК, МАШИНА, ПОМЕЩЕНИЕ, КОСМИЧЕСКИЙ АППАРАТ являются типами. Определенная структура, заданная на множестве типов, называется схемой базы данных. В общем виде схема базы данных показана на рис. 2.1.
Рис 2.1. Общий вид схемы базы данных о предметной области
На практике связи между типами объектов в базах данных могут быть на много сложнее, чем показано на данном рисунке. В этих случаях используется специальный механизм ссылок (переходов от одного типа к другому). Пример фрагмента схемы базы данных отражающий предметную область “помещения некоторого учебного заведения” показан на рис. 2.2.
Рис 2.2. Схема фрагмента базы данных, отражающего помещения высшего учебного заведения
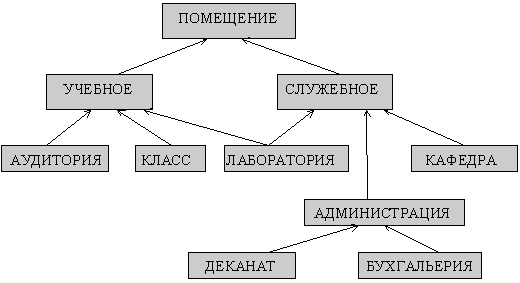
В данном примере в каждом прямоугольнике указан определенный тип объектов. Эти же типы объектов можно описать и в терминах теории отношений, изложенных в предыдущем разделе. Пример.
ЕСТЬ(помещение,
(учебное Ъ служебное)), ЕСТЬ(помещение_учебное, (аудитория Ъ класс Ъ лаборатория )) или ЕСТЬ(ЕСТЬ(помещение, учебное), (аудитория Ъ класс Ъ лаборатория )).Легко заметить, что все подчиненные типы объектов представляют собой значения определенных свойств вышестоящих типов. Поэтому для корневого (заглавного) типа можно составить базу свойств
S1, S2, ..., Sn и определить для каждого свойства Si соответствующий показатель Xi с областью значений Ai. При этом любой объект данного типа будет определяться отношение Q(x1,x2,...,xn), где xiОAi. Так в данном примере можно определить:S1 - назначение помещения, X1 - наименование специализации помещения, А1={учебное, служебное, - };
S2 - специализация учебных помещений, X2 - наименование специализации, А2={лекции, занятия, опыты, - };
S3 - специализация служебных помещений, X3 - наименование специализации, А3={администрация, делопроизводство, преподавательская, - }. Знак “- ” здесь будет указывать на то, что свойство Si не относится к данному объекту. Используя приведенные выше определения, получим таблицу 2.6, содержащую описание той же предметной области, которая была представлена на Рис. 2.2.
По существу каждая строка данной таблицы представляет собой элемент
Q(x1,x2,...,xn) универсума U= {A1ґ A2ґA3}, то есть представляет собой код (или обобщенный код) помещения определенного типа. Таким образом, мы рассмотрели способ представления баз данных в форме таблиц обобщенных кодов. Полезность такой формы представления видна из следующего маленького примера.Пример. Из таблицы 2.6 следует, что свойства S2 и S3 отнесены к различным объектам. Но эти свойства не являются независимыми. Фактически множества А2 и А3 являются подмножествами значений одного и того же свойства. Поэтому свойства S2 и S3 можно заменить одним свойством S’2 - “специализация помещения” с областью значений A’2 = {лекции, занятия, опыты, администрация, делопроизводство, преподавательская}. В результате структура базы данных существенно упрощается. При необходимости в таблицу2.6 можно легко добавить любое количество новых свойств рассматриваемых объектов, например номер помещения, площадь помещения, освещенность и так далее. Важно то, что действия над элементами базы данных, такие как поиск, сравнение, сортировка по значениям заданных свойств и т.д., можно выполнять путем формальных операций над соответствующими обобщенными кодами. Особенно широкие перспективы при этом открываются для реализации механизмов логического вывода.
Пример. Рассмотрим еще раз базу данных (фактов), приведенную в предыдущем разделе. Судя по содержащимся там фактам, можно заметить, что все они определяют свойства объектов одного тип - человек. Эти свойства определяются как: S1 - наличие имени, S2 - наличие пола и S3 - способность быть родителем. Для характеристики этих свойств используются соответствующие переменные: X1 - имя с областью значений A1 = {Петр, Иван, Фома, Ольга, Марья}, X2 - пол с областью значений A2 = {мужчина, женщина} и X3 - отношение РОЛИТЕЛЬ(X1) с областью значений A3 = {да, нет} или A3 = {РОДИТЕЛЬ(X1), НЕ_РОДИТЕЛЬ(X1)}. Частными случаями типа человек является типы: отец, мать и не_родитель. Эти типы является конкретизацией типа человек по имени (S1), полу (S2) и по наличию ребенка (S3). Согласно имеющимся в базе данных фактам объекты типа отец и мать определяются следующими высказываниями:
отец
( - , мужчина, РОДИТЕЛЬ(X1)),мать
( - , женщина, РОДИТЕЛЬ(X1)).
Эти высказывания являются обобщенными кодами по свойству
S1 – имя человека. Легко заметить, что обобщенный коды отец и мать представляют собой значения логической функции F(X1, X2,X3), определенной на множестве объектов типа человек. С учетом данных определений вышеупомянутая база фактов представляется следующей таблицей:
Применяя операцию пересечения к обобщенному коду с именем отец с остальными кодами таблицы 2.7 получим единственное решение:
отец (Петр, мужчина, РОДИТЕЛЬ(Иван)).
Таким образом, посредством операции пересечения обобщенных кодов реализован дедуктивный вывод о том, что Петр приходится отцом Ивану. Таким же способом можно реализовать и любой индуктивный вывод. Следует заметить, что представление баз данных в форме таблиц обобщенных кодов во многом сходно с формами представления реляционных баз данных. Сходство это состоит в том, что, как и реляционная база данных, таблица обобщенных кодов содержит описание определенных отношений между свойствами объектов. Однако для построения таблицы обобщенных кодов предъявляются более строгие требования к определению свойств и их областей значений. Эти требования необходимы для формализации теоретико-множественных и логических операций над отношениями, представленными в кодовой форме.
Логические функции2.9.1. Определения и формы представления логических функций
Отличительная особенность логических функций состоит в том, что области определения самих функций и их аргументов являются дискретными конечными множествами. Обычно это множества истинности определенных высказываний или отношений, представляющих собой предикаты
pe. Например, областью значений логической функции может быть множество {(x<a), (x>a), (x=a)}, где каждое выражение в круглых скобках представляет собой утверждение об истинности определенного отношения.Определения
:1. Пусть
Xi переменная, принимающая значения из множества Ai={a1(i),...,ak(i)}, тогда логическая функция F(X1,...,Xn) есть однозначное отображение {A1ґA2ґAn} ® AF, где AF - область значений функции F(X1,...,Xn). Вместо F(X1,...,Xn) будем писать также F(X).2. Если логическая функция и ее аргументы (переменные
Xi) принимают значения из одного и того же множества A, содержащего k различных значений, то эта функция называется однородной k-значной логической функцией, или логической функцией класса Pk.3. Логические функции класса
P2, с множеством значений E={ИСТИННО,ЛОЖНО}, называются двоичными или булевыми логическими функциями, если они определены на множестве аксиом, содержащихся в таблицах 2.8 и 2.9, и только на них. В этих таблицах приняты следующие обозначения: ИСТИГННО=1, ЛОЖНО=0.Таблица 2.8. Булевы функции одной переменной
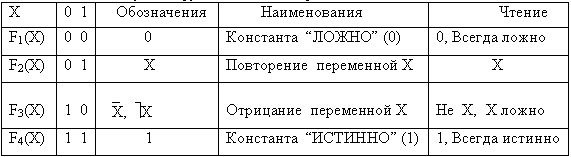
Таблица 2.9. Булевы функции двух переменных
Наиболее общей универсальной формой представления логических функций являются таблицы. Кроме того, существует много различных алгебраических форм представления логических функций, основанных на использовании функционально полных систем аксиом (элементарных функций
), специально определяемых для каждого класса логических функций. Доказано, что из перечисленных булевых функций одной и двух переменных можно составить несколько функционально полных систем, пригодных для формального представления любой n-местной булевой функции. Наиболее популярной функционально полной системой булевых функций является система, состоящая из константы 0, константа 1, отрицания ` X1, конъюнкции X1Щ X2 и дизъюнкции X1Ъ X2. Существуют две формы представления логических функций с использованием этой системы: дизъюнктивная, представляемая в видеи конъюнктивная, формула которой имеет вид
где ~Xi означает, что переменная Xi может входить в данную формулу, как со знаком отрицания, так и без него.
4. Если функция
F(X1, ..., Xn) принимает значения из множества AF = {f1, f2,...,fe,...,fk,q }F, где q - нулевое (пустое) значение, то функция F(X1, ..., Xn)fe, принимающая значение fe только на одном из наборов значений переменных X1, ..., Xn и принимающая значение q на всех остальных наборах этих переменных, называется конституентой функции F(X1,...,Xn)5. Функция F(X1, ..., Xn)fe, принимающая значение fe на нескольких наборах значений переменных X1, ..., Xn и принимающая значение q на всех остальных наборах этих переменных, называется импликантой функции F(X1, ..., Xn). По данным определениям конституента есть частный случай импликанты.
6. Логические функции, допускающие неравенство Ai№Ae, i,e
О{1, ..., n, F}, называются неоднородными логическими функциями или функциями общего класса Po.По данным определениям логические функции класса
Pk являются частным случаем функций класса Po. Разработка теории логических функций класса Po до настоящего времени еще не завершена. И все же, имеющиеся в этой области результаты уже сейчас могут быть эффективно использованы для моделирования сложных алгоритмических процессов и систем [14]. В дальнейшем мы будем рассматривать в основном формальные построения логических функций класса Po, сравнивая их, при необходимости, с аналогичными формальными построениями в классе булевых функций.2.9.2. Формальные представления логических функций класса P
oДля логических функций общего класса также существует проблема их формального представления. Чтобы решить эту проблему начнем с описания табличной формы представления этих функций. Общий вид такой формы представляет собой таблица 2.10.
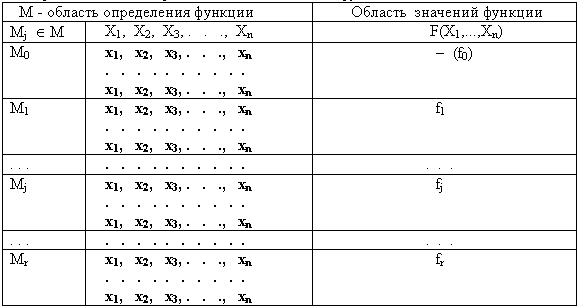
Таблица 2.10. Форма табличного представления логических функций общего класса
В
этой таблице показано, что все множество определения функции F(X1,...,Xn) в общем случае делится на r+1 подмножество Mj, j=0,1,...r, наборов значений переменных X1,...,Xn. Каждый набор представляет собой кортеж q = (x1,...,xn), где xiОAi, Mj - подмножество кортежей, на которых функция F(X1,...,Xn) принимает значение fj. На подмножестве M0 функция F(X1,...,Xn) не определена, иначе говоря, F(X1,...,Xn) принимает значение f0= - . Логические функции, для которых M0 = , называются полностью
определенными. В противном случае они называются
не полностью определенными, или не
доопределенными. Предполагается,
что каждое множество Ai
представляет собой полную группу несовместных
высказываний, то есть, предполагается, что
вероятность того, что переменная Xi одновременно примет какие-либо два
значения из множества Ai
равна нулю. Такое же предположение принимается и
для области значений функции F(Х).
Предполагается также, что множества Mj не пересекаются. Эти предположения
позволяют получить строго однозначное и
корректное определение логических функций
общего класса. При указанных условиях для любой
логической функции справедливы
соотношения:
Эти соотношения задают дизъюнктивную форму представления логической функции общего класса.
Учитывая, что любое подмножество
Mj может быть представлено соответствующим объединением обобщенных кодов
, где t номер
обобщенного кода, из числа кодов, представляющих
подмножество Mj, из
соотношений (2.6) непосредственно
получим форму представления логических функций
общего класса с помощью обобщенных кодов:
В дальнейшем будем называть ее кодовой дизъюнктивной нормальной формой
(КДНФ) представления логических функций.Табличный вид кодовой формы логической функции общего класса показан в таблице2.11.
Таблица 2.11. Форма табличного представления логических функций общего класса
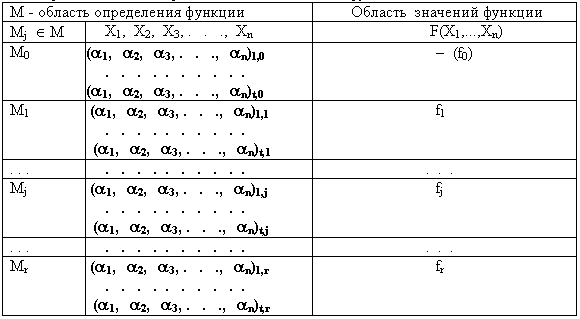
Доказательство того, что любая функция класса
Po может быть представлена в КДНФ, следует из только что изложенного вывода формулы 2.7 из табличной формы, которая, как известно, является универсальной формой представления любых функций. Кроме табличных форм представления логических функций существуют и алгебраические формы, основанные на использовании различных функционально полных систем. Наиболее распространенными алгебраическими формами являются так называемые дизъюнктивные и конъюнктивные нормальные формы (КНФ и ДНФ). Общие принципы построения ДНФ логических функций общего класса следующие:Данное выражение
называется совершенной дизъюнктивной
нормальной формой (СДНФ)
логической функции общего
класса. Это одна из возможных алгебраических
форм представления логических функций.
Фактически она, как и совершенная кодовая
дизъюнктивная нормальная форма, совпадает с
табличной формой представления этой же функции,
так как каждая дизъюнкция 
соответствует
кортежу pt. По определению таблица
2.10 и СДНФ должны содержать 
кортежей q,
где ki - значность переменной Xi. Ясно,
что такие формы представления функций с большим
числом переменных не экономичны и трудно
обозримы. Поэтому в теории и практике применения
логических функций изобретено много способов
более экономного представления этих функций. Эти
способы обычно основаны на минимизации
совершенных (полных) нормальных форм
представления логических функций.
2.9.3. Принципы минимизации кодовых форм представления логических функций
Удобство восприятия и использования форм представления логических функций, как мы уже говорили, во многом зависит от их размеров и структурной сложности. Исходная, так называемая совершенная кодовая дизъюнктивная нормальная форма (СКДНФ) фактически ничем не отличается от таблиц 2.10. Поэтому она так же неэкономична, как и эта таблица. Однако вышеизложенная теория обобщенных кодов позволяет предложить достаточно простые формализованные алгоритмы решения проблемы минимизации КДФ логических функций любого класса. Один из таких алгоритмов минимизации КДНФ логических функций общего класса рассматривается в данной книге.
Алгоритм основан на следующих теоретических принципах.
F(X1,...,Xn)fj = (Mj® fj)Ъ(Mq ® q ), (2.13)
где
j=1,...,r, Mq = M \ Mj, MjЗMq = . Поэтому
для задания импликанты F(X1,...,Xn)fj
такой функции достаточно в
какой-нибудь форме задать только одно из
указанных подмножеств. Другими слова, ее можно
представлять как
F(X1,...,Xn)fj = Mj® fj, (2.14)
или как
щF(X1,...,Xn)fj = Mq ® q . (2.15). При этом
одно и то же подмножество Mj, в общем случае, может быть
представлено различными объединениями
различных обобщенных кодов, и проблема состоит в
том, чтобы представить подмножество Mj объединением обобщенных кодов,
содержащим наименьшее число непустых значений
переменных Xi. Формальная
математическая постановка этой проблемы состоит
в следующем. Дана табличная форма импликанты F(X1,...,Xn)fj = Mj®fj,
j=1,...,r. Найти кодовую нормальную
форму этой импликанты:
соответствующую минимальному значению оценочной функции
где r(Kt,j) - число разрядов обобщенного кода Kt, не содержащих знак “- ”, то есть заполненных какими-либо значениями, кроме значения тире, s - число обобщенных кодов, входящих в КДНФ импликанты F(X1,...,Xn)fj.
При ее минимизации подмножество M0 может быть использовано для увеличения количества свободных разрядов (разрядов со знаками тире) в обобщенных кодах Kt,j за счет добавления к подмножествам Mj некоторых кортежей из подмножества M0. В связи с тем, что функция F(X1,...,Xn) не определена на подмножестве M0, предполагается, что его элементы (кортежи) можно добавлять к подмножествам Mj произвольно, то есть в любом количестве и в любом порядке. При этом для каждой импликанты F(X1,...,Xn)fj будет получена СКДНФ вида:
и может быть найдена соответствующая ей минимальная КНФ (МКДНФ)
(2.20) где K*t - обобщенный код, объединяющий некоторые элементарные коды из подмножества (MjИM*0).
Алгоритм приближенной минимизации КДФ импликанты F(X1,...,Xn)fj логической функции общего класса можно построить на следующих принципах.
При этом g(r)j = min.
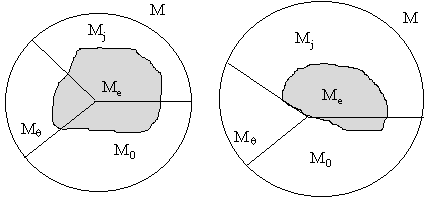
Другими словами, объединение 
является кодовым
покрытием множества Mj, обладающим минимальным количеством заполненных разрядов. Примерная схема такого покрытия показана на
Рис.2.4. Пример покрытия множества Mj обобщенными кодами K*t,j
Учитывая изложенное, поиск приближенно минимальной КДНФ предлагается осуществлять в следующем порядке:
- найти код K*1,j, покрывающий наибольшее число кортежей из Mj,
- затем таким же способом найти код K*2,j, покрывающий наибольшее число кортежей из подмножества Mj\ M*1,j,
- и так далее, пока не выполним условие
Mj\(M*1,jИ M*2,jИ ...ИM*s,j) =
При этом искомая приближенно минимальная КДНФ будет иметь вид:
K*2,j И K*2,j И ... И K*2,j.
Для оценки степени приближения произвольно взятого обобщенного кода Ke к коду K*t,j, пригодному для включения его в искомую минимизированную КДНФ, предлагается использовать следующие оценочные функции (показатели):
где x ( Ke) - показатель, характеризующий положение подмножества Me, представленного кодом Ke, относительно подмножеств Mj и Mq в области М определения функции F(X1,...,Xn)fj а r(Ke) - показатель количества заполненных разрядов в обобщенном коде Ke. Величина x ( Ke) / r(Ke) показывает какая доля оценки x ( Ke) приходится на один заполненный разряд обобщенного года Ke. Чем больше эта величина, тем предпочтительнее включение кода Ke в искомую КДНФ.
Предлагаемый алгоритм рассмотрим на примере функции
F(X12, X22, X33, X42)3, заданной таблицей обобщенных кодов (таблица 2.12). Верхние индексы у символов переменных и у закрывающейся скобки соответственно обозначают значность переменных Xi и функции F(X). Общее количество кортежей, составляющих область определения данной функции равно величине
Однако в таблице 2.12
заданы только те кортежи, которым соответствуют
определенные значения функции F(X12,
X22, X33, X42)3,
fj О {1, 2, 3}.
Кортежи, на которых функция не определена и
может иметь любое значение, в таблице
отсутствуют. Они считаются заданными “по
умолчанию”. Таким образом, достигается
сокращение исходной таблицы.
Таблица 2.12 Таблица 2.13
Суть алгоритма состоит в следующем:
И (0 0 1 - ) = (0 0 0 0) И (0 0 1 - ).2.1. Составить таблицу КДНФ импликанты F(X)fj. В нашем примере это таблица 2.14, представляющая импликанту F(X)f1. Будем называть ее исходной таблицей.
2.2. Проверить ортогональность обобщенных кодов исходной таблицы (2.14). Если все обобщенные коды заданной таблицы ортогональны, то перейти к следующему пункту, иначе выполнить ортогонализацию заданных обобщенных кодов. В таблице 2.14 не ортогональны между собой только два первых обобщенных кода: (0 0`2 0) и (0 0 1 - ). Над ними необходимо выполнить следующие действия:
(0 0`2 0) \ (0 0 1 - ) = (0 0 0 0),
(0 0`2 0)
Ортогонализация обобщенных кодов необходима для корректного подсчета значений оценочной функции x (Ke). Количество n(Mh) кортежей, соответствующих обобщенному коду в каждой строке ортогонализованной таблицы (2.15) показаны в первом столбце этой таблицы.
где n(a i) - мощность подмножества
значений переменной Xi, представленного
символом a i в коде Kh, h -
номер строки данной таблицы.
Таблица 2.14 Таблица 2.15
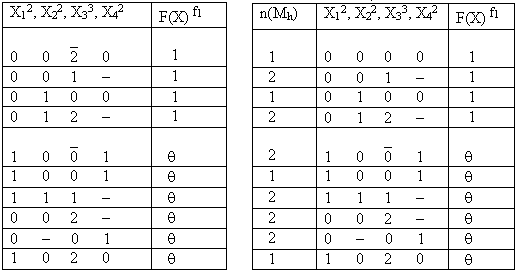
2.3. Для базы переменных (X12, X22, X33, X42) импликанты F(X)f1 составить все возможные обобщенные коды с одним заполненным разрядом - коды K(1)e. При этом для получения более глубокой минимизации целесообразно использовать не только положительные значения переменных Xi, но также и отрицания этих значений. Смотрите пример,
Tаблица 2.16. Таблица 2.17
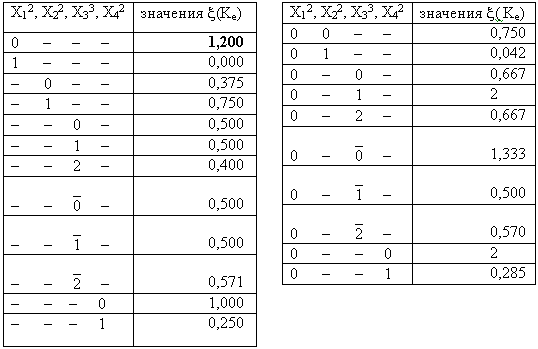
2.4. Для всех кодов K(1)e вычислить значения показателя x (Ke). Для рассматриваемого примера результаты вычислений приведены в таблице 2.16. Покажем процедуру вычислений на примере для случая, когда K(1)e= (0 - - - ). При этом
M(1)eЗM1= (0 - - - )З [(0 0 0 0)И(0 0 1 - )И(0 1 0 0)И(0 1 2 - )]=M1, n(M1)=6;
M(1)eЗMq=[(0 0 2 - )И(0 - 0 1)], n(M(1)eЗMq)=4;
x (0 - - - )=6 / 1+4= 1,200.
2.5. Найти максимальное значение показателя x (K(1)e) и соответствующий ему код K(1)e. В данном случае это код K(1)e = (0 - - - ) со значением x(K(1)e)=1,200.
2.6. Проверить, удовлетворяет ли код K(1)e условию n(MeЗMq) =
2.7. Повторить все действия указанные в пунктах 2.4, 2.5 и 2.6 с кодами K(2)e, то есть вычислить для этих кодов значения показателя x (K(2)e), найти максимальное из этих значений, определить соответствующий ему код K(2) e и проверить условие n(Me З Mq ) =
2.8. Из таблицы, задающей импликанту
F(X)f1 (таблица 2.15 рассматриваемого примера), вычесть код K*1,j (K*1,1). В результате получается исходная таблица для поиска следующего обобщенного кода подходящего для искомой КДНФ. В нашем примере это таблица 2.18.2.9. С таблицей 2.18 повторить все действия, которые выполнялись с таблицей 2.15 и найти следующий обобщенный код K*2,j (K*2,1), подходящий для искомой КДНФ. Читателю предлагается проделать эту работу самостоятельно и убедиться, что следующим будет получен код K*2,1 = (- 1 2 - ).
Таблица 2.18 Таблица 2.19
2.10. Вычесть код
K*2,j из таблицы 2.18 и составить новую исходную таблицу для поиска следующего обобщенного кода K*t,j. В данном примере это будет код K*3,j = (- - 0 0).2.11. Продолжать перечисленные выше действия до тех пор, пока при очередном вычитании кода
K*t,j из таблицы, по которой он был получен, подмножество Mj окажется пустым, то есть в результате вычитания в таблице не останется ни одного кода, представляющего кортежи из этого подмножества. Другими словами, пока не будет выполнено условие: Mj\(M*1,jИM*2,jИ... ИM*s,j)=F(X)fj = (K*1,j И K*2,j И ... И K*s,j) ® fj.
В нашем примере
F(X) f1 = (0 - 1 - )И(- 1 2 - )И(- - 0 0) ® 1.
F(X) f2 = (1 0 - 1) ® 2 и
F(X) f3 = (1 1` 0 - )И(0 - 0 1)И(- 0 2 0) ® 3.
Приведенный алгоритм легко формализуется и может быть полезен при решении многих логических задач и при моделировании сложных процессов.
Вероятностные логические функции общего класса 2.10.1. Формальное представление вероятностных логических функцийВ традиционной математической логике логические переменные X
i считаются детерминированными, то есть предполагается, что переменные Xi принимают, или не принимают определенное значение aeОAi в определенных условиях с вероятностью равной единице. В действительности же, как правило, реальные события носят случайный характер. Поэтому отражающие эти события переменные Xi следует рассматривать как вероятностные переменные, принимающие значения aeОAi с соответствующими вероятностями V(Xi = ae). По определению логической переменной Xi должно выполняться условие:вытекающее из свойства несовместности значений
aeОAi. Данная интерпретация логических переменных требует разработки соответствующего математического аппарата вероятностной логики. В качестве теоретической основы для формального представления вероятностных логических функций целесообразно взять уже знакомый нам формализм логических функций общего класса. Тогда вероятностной логической функцией общего класса будет называться логическая функция общего класса F*(X1k1, ..., Xnkn)kF, определенная на базе вероятностных логических переменных X1k1, ..., Xnkn и принимающая значения fjОAF с вероятностями V(F* = fj), которые определяются как вероятности сложных событий:где
j = 1,...,N, gj - номер конъюнкции в подмножестве конъюнкций, связанных с j-тым значением функции F*(X1k1, ..., Xnkn) kF. Из данного определения следует, что для представления вероятностных логических функций могут быть использованы все рассмотренные выше формы представления логических функций общего класса дополненные таблицами распределения вероятностей V(Xi = ae) значений переменных Xi.Пример. Вероятностная логическая функция
F*(X13, X23, X32)3 представлена двумя таблицами: 2.20 и 2.21. В таблице 2.20 задана ее сокращенная КДНФ, а в таблице 2.21 задано распределение вероятностей значений ее аргументов Xi.Таблица 2.20 Таблица 2.21
При этом вероятности значений функции
V(F* = fj) могут быть вычислены по теореме сложения вероятностей. Эффективный алгоритм решения этой задачи предложен автором [14].2.10.2. Вычисление вероятностей значений вероятностных логических функций
Если логическая функция представлена совершенной дизъюнктивной нормальной формой или совершенной кодовой нормальной формой, то формулы для вычисления вероятностей ее значений по заданным вероятностям значений ее аргументов Xi имеют следующий вид:
Они получаются из совершенных дизъюнктивных нормальных форм импликант F*(X)f(j) после замены значений aeОAi логических переменных Xi на соответствующие значения вероятностей V(Xi = ~ae,i) и замены логических символов “U ” и “U ” на соответствующие им арифметические символы умножения и сложения. Символ ~ae,i означает, что ~ae,i I { ae,i, ` ae,i}. Если же вероятностная логическая функция задана сокращенной дизъюнктивной нормальной формой или сокращенной КДНФ, то такое непосредственное преобразование возможно, только тогда, когда заданная ДНФ представлена ортогональными дизъюнктивными членами (конституентами) или ортогональными обобщенными кодами K*e,j. Для преобразования ортогонализованной КДНФ логической функции в соответствующую ей формулу для вычисления вероятностей ее значений достаточно выполнить вышеизложенную замену символов логических операций на символы арифметических операций и замену логических значений переменных на значения их вероятностей. Эту операцию будем называть правилом замены по аналогии. В общем виде ее можно представить как отношение:
Заметим, что в случае, когда переменная
Xi имеет отрицательное значение Xi = ` ae,i, то соответствующая вероятность V(Xi = ` ae,i) вычисляется по формуле:и по определению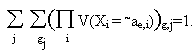 
На основе изложенных положений предлагается следующий алгоритм преобразования любой КДНФ логической функции в соответствующую ей формулу для вычисления вероятностей значений данной логической функции по заданным вероятностям значений ее аргументов.
Пример. Вычислить вероятность значений логической функции общего класса, заданной таблицами 2.20 и 2.21. Таблица 2.20 представляет собой КДНФ логической функции
F*(X13, X23, X32)3. В данной таблице имеются неортогональные обобщенные коды:(1, 2, - ) и (-, 2, 1), а также
(`0, `2, 0) и (2, -, 0).После их ортогонализации получим таблицу 2.22 эквивалентную таблице 2.21 в том смысле, что обе эти таблицы задают одну и ту же логическую функцию
F*(X13,X23,X32)3. В результате применения к таблице 2.22 правила замены по аналогии получим следующие формулы для вычисления вероятностей значений заданной логической функции:V(F*=0) = V(X13=0) + V(X13=1) * V(X23=2) + V(X13=2) * V(X23=2) * V(X32=1);
V(F*=1) = [1 - V(X13=0)] * [1 - V(X23=2)] * V(X32=1);
V(F*=2) = V(X13=1) * [1 - V(X23=2)] * V(X32=0) + V(X13=2) * V(X32=0).
После подстановки соответствующих значений вероятностей из таблицы 2.21 в эти формулы получим:
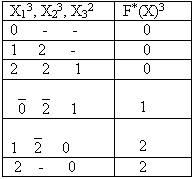
V(F*=0) = 0,238;
V(F*=1) = 0,504;
V(F*=2) = 0,258.
Заметим, что значения
логической функции, как и значения ее аргументов,
представляют собой несовместные события и их
вероятности связаны соотношением:
Согласно определению, данному в математической энциклопедии
[13] алгоритм есть точное предписание, которое задает вычислительный процесс нахождения значений вычислимой функции по заданным значениям ее аргументов. Соответственно алгоритмический процесс есть последовательность действий, выполняемых некоторым исполнителем по заданному алгоритму. Классическими примерами алгоритмических процессов являются процессы образования слов из заданного алфавита по определенным правилам. Однако, если под алфавитом понимать символы некоторых материальных или идеальных объектов, то алгоритмический процесс можно рассматривать как последовательность действий, выполняемых над объектами любой природы по точно определенной инструкции. Поэтому практическая значимость алгоритмов и алгоритмических процессов не ограничивается одними вычислительными задачами. Математическая строгость и точность алгоритмов обеспечивает возможность автоматизации задаваемых ими алгоритмических процессов в различных областях деятельности человека, в том числе и в творческом мышлении. В качестве теоретических моделей машин, имитирующих алгоритмические процессы, обычно рассматривают машины Тьюринга, фон-Неймана и конечные автоматы. Между алгоритмами и алгоритмическими процессами существует связь, показанная на рисунке 2.5.Рис. 2.5. Связь между алгоритмом и алгоритмическим процессом
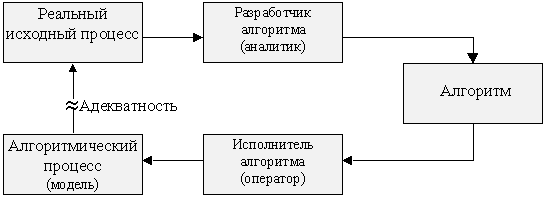
На этом рисунке показано, что любой алгоритмический процесс, полученный при реализации алгоритма, является моделью некоторого реального процесса. Степень соответствия алгоритмического процесса (модели) реальному исходному процессу называется адекватностью
. Таким образом, по определению алгоритм есть статический информационный объект (инструкция), представленная на некотором языке, понятном для потенциального исполнителя. Алгоритмический процесс есть динамический физический объект, представляющий собой упорядоченные действия некоторого исполнителя, выполняемые по заданному алгоритму. Любой алгоритмический процесс характеризуется следующими свойствами:Результативность - означает, что алгоритмический процесс реализует определенную целевую функцию
X® Y за конечное число шагов (действий) или за конечный отрезок времени, где X - множество исходных данных, а Y - множество результатов выполнения данного задания.Массовость - означает возможность существования множества исходных данных {
x1…xn} из которого могут быть взяты исходные данные xt для инициализации алгоритмического процесса. Каждому набору xi исходных данных соответствует один вполне определенный результат yj. Однако, один и тот же результат может соответствовать нескольким наборам исходных данных.Дискретность
- означает, что алгоритмический процесс состоит из отдельных действий, процедур или операций, связанных между собой определенными причинно следственными связями.Детерминированность
следует из того, что последовательность действий в алгоритмическом процессе точно определена заданным алгоритмом.Адекватностью
называется степень соответствия алгоритмического процесса (модели) реальному исходному процессу, являющемуся прообразом данного алгоритмического процесса. Характеристика всей совокупности действий и причинно следственных связей между ними в алгоритмическом процессе называется его структурой. Пусть D - множество всевозможных действий в алгоритмическом процессе. Тогда однозначно определенное отношение D® D есть структура S алгоритмического процесса. Структура S является основной характеристикой сущности алгоритмического процесса. Каждый алгоритмический процесс имеет свою структуру S.Самоуправляемость
алгоритмического процесса характеризуется наличием в алгоритмическом процессе специальных действий duОD, предназначенных для управления последовательностью функциональных действий dfОD (вычислительных, механических, информационных, и так далее), предназначенных для непосредственной реализации целевой функции X® Y. Действия du делятся на два типа: условные переходы (распознаватели истинности определяющих условий Pе ) и безусловные переходы от текущего действия к следующему. Безусловные переходы обычно обозначаются в схемах алгоритмов стрелкой (® ), или последовательной записью описателей выполняемых действий друг за другом. Запись D® D означает, что множество действий D упорядочено определенным образом так, что все действия dОD связаны между собой условными и безусловными переходами. Вообще говоря, безусловные переходы следует рассматривать как, частный случай условных переходов, du : = d(P)® , du : = ® , если условие P заключается в завершении текущего действия, или вообще отсутствует.Альтернативность - означает, что функция
X® Y может быть реализована несколькими различными алгоритмическими процессами (АП). Два АП реализующих одну и ту же функцию X® Y называют эквивалентными. Из эквивалентности АП следует эквивалентность соответствующих им структур и алгоритмов. При разработке алгоритмических процессов и алгоритмов стараются получить наиболее простой и экономичный алгоритмический процесс из всех возможных эквивалентных АП, реализующих заданную функцию X® Y.Сложность
алгоритмического процесса есть характеристика многообразия (разнообразия) действий, составляющих этот процесс, и структурных связей между ними. Более подробно это понятие будет рассмотрено в следующем разделе.Ресурсоемкость алгоритмического процесса оценивается величиной времени, необходимого на реализацию целевой функции
X® Y и количеством затрачиваемых на это ресурсов (памяти, специальных устройств, математического обеспечения и т.д.).Алгоритм, как правило, представляет собой описание множества
D действий алгоритмического процесса и его структуры S на некотором формализованном языке.Всеобщими свойствами алгоритмов являются
:Все перечисленные свойства имеют хорошо определенные показатели и могут использоваться для оценки качества разрабатываемых алгоритмов и алгоритмических процессов.
2.11.2. Математические модели алгоритмических процессов
В зависимости от целей моделирования модели алгоритмических процессов могут характеризовать любые вышеперечисленные свойства. При разработке алгоритмов обычно используют модели для оценки структурных, точностных, временных и ресурсных показателей свойств алгоритмов и алгоритмических процессов. Особо следует отметить класс структурных моделей АП. Обычно они представляют собой формализованные описания отношения
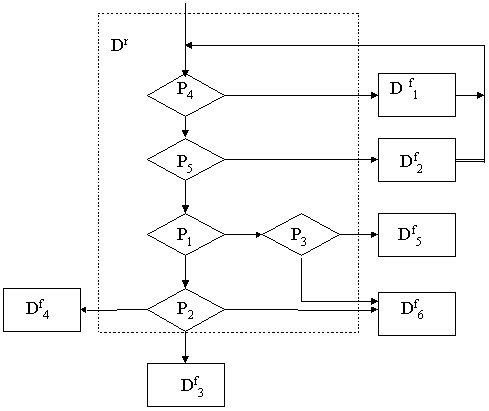
D ® D. В специальной научной литературе они известны как логические схемы алгоритмов (схемы Ляпунова), схемы программ Янова, канонические схемы алгоритмов Блохе - Неверова, схемы алгорифмов Маркова и схемы типовых алгоритмических процессов [14]. Сюда же могут быть отнесены и многочисленные математические модели конечных автоматов. Любую такую схему можно рассматривать как систему отображений множества Dr действий - распознавателей истинности условий Pe в множество Df действий - преобразователей и отображения множества Df обратно в множество Dr. Формальная запись этой системы имеет вид: Dr® Df ® Dr. Символом Pe будем обозначать набор (конъюнкцию) условий из множества P, определяющих е-тый переход в алгоритмическом процессе. При этом отношение P® Df будем называть характеристической функцией структуры алгоритмического процесса (ХФ). Действия - преобразователи Dfj из Df обычно записывают в виде определенных математических выражений. Стрелка “® ” обозначает здесь множество безусловных переходов в алгоритмическом процессе. Пусть F(p1, p2,...,pn)D(f) многозначная логическая функция общего класса, имеющая аргументы p1, p2,...,pn, область определения P и область значений Df. Аргументы p1, p2,...,pn представляют собой элементарные предикаты. Тогда математическую модель алгоритмического процесса можно изобразить в виде схемы, показанной на рис. 2.6. На схеме затемненным прямоугольником обозначено множество всех действий распознавателей условий Pi, а подмножества Dfj действий преобразователей из множества Df представлены светлыми прямоугольниками. Информационные потоки на схеме изображены удвоенными стрелками, а простыми стрелками обозначены безусловные переходы между действиями.Рис. 2.6. Схема (модель) типовой логической структуры алгоритмического процесса
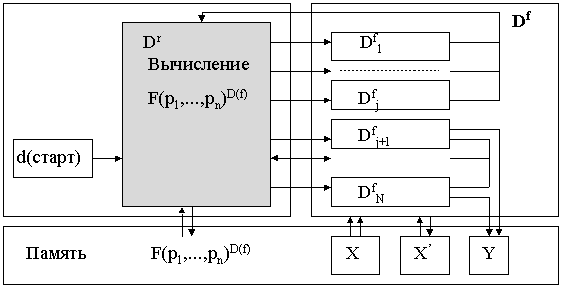
Подмножества Dfj состоят из действий непосредственно связанных друг с другом безусловными переходами в одну последовательность, или составляющих отдельный алгоритмический процесс (подпроцесс), рассматриваемый в данном случае, как одно целое. Множества действий Dfj бывают промежуточные и заключительные. В результате промежуточных действий выполняются определенные преобразования данных из множества X и преобразование значений предикатов Pi, определяющих условия перехода к следующему действию Dfj. После выполнения промежуточных действий осуществляется переход к следующим действиям распознавателям, а в результате выполнения заключительных действий получают искомое решение Y, и алгоритмический процесс останавливается. В приведенной модели структура алгоритмического процесса отличается тем, что все условные переходы определяются в результате вычисления значений одной обобщенной логической функции F(p1,...,pn)D(f), называемой характеристической функцией алгоритмического процесса. Каждый такой переход ведет к промежуточному, или к заключительному подмножеству действий Dfj. После выполнения любого промежуточного подмножества действий Dfj осуществляется переход к вычислению очередного следующего значения характеристической функции. После выполнения заключительных действий получается определенный результат и алгоритмический процесс заканчивается. Описанная структура алгоритмического процесса называется типовой [14]. Соответственно алгоритмический процесс с такой структурой называется типовым алгоритмическим процессом (ТАП). Важным достоинством типовых алгоритмических процессов является возможность формализации анализа и синтеза их структуры. Эта возможность следует из того, что характеристическая функция ТАП может быть легко представлена в кодовой ДНФ и для ее анализа и эквивалентного преобразования может быть эффективно применен аппарат теории обобщенных кодов.
2.11.3. Пример синтеза структуры типового
алгоритмического процессаПусть нам поставлена задача разработать алгоритмический процесс и алгоритм для решения на ЭВМ задачи вычисления действительных корней квадратного уравнения
ay2+by+c=0 по заданным значениям коэффициентов a, b, c. Методика решения этой задачи общеизвестна. Суть методики состоит в следующем.4. В противном случае проверить условие P3: (a = 0)Щ(b№ 0). Если оно истинно, то применить формулу:
Эта методика еще не является алгоритмом, так как в ней не определена строгая последовательность действий, не оговорены условия начала и окончания процесса и другие атрибуты алгоритма. Чтобы превратить эту методику в алгоритм типового алгоритмического процесса поступим так:
Полученную характеристическую функцию проверим на непротиворечивость (корректность) и на
полноту ее определения. Для этого введем следующие сокращенные обозначения для значений переменных: p1={0, 1}, p2={0, 1, 2}, p3={0, 1}, p4={0, 1}, и для значений функции Dfj = {1, 2, 3, 4, 5, 6}, соответствующие значениям, определенным ранее. Тогда таблица 2.23 превратится в более удобную для формального анализа таблицу 2.24, где P - переменная, принимающая значения из множества М всех возможных наборов значений переменных p1,..., p4. Каждый такой набор PeI M есть формальное выражение условия, определяющего переход к соответствующим действиям Dfj. Если Pe истинно, то выполнить переход к Dfj.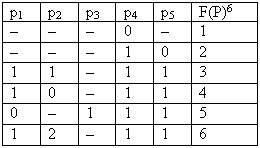
Данная таблица представляет собой корректно определенную логическую функцию общего класса
F(p21, p32, p23, p24, p25)6 и является ее минимальной кодовой ДНФ, так как каждая ее импликанта представлена только одним обобщенным кодом. Однако данная функция может быть определена не полностью. Для проверки полноты ее определения вычислим полную мощность ее области определения по формуле: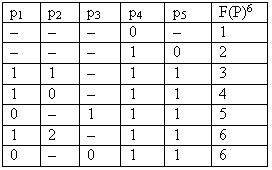
где ki - мощность области
значений переменной pi (число элементов
множества Ai). В данном примере n(M) = 2* 3* 2*
2* 2= 48. Затем
следует вычислить мощность n(M’) той части M’
области определения характеристической функции,
где она определена. Эта часть представлена таблицей 2.25. Если в данной таблице все
обобщенные коды ортогональны, как в данном
случае, то 
где m(M*e) - мощность
подмножества M*e элементарных кодов
(наборов значений переменных pi)
представленных обобщенным кодом Ке в
данной таблице. Напомним, что 
где n(a
i) - число значений, которые переменная pi
может принимать в обобщенном коде Ке.
Например, для кода К2 = ( - - - 0 1) в нашем примере m(M*e)
= 2* 3* 2* 1*
1 = 12. В целом для таблицы 2.25 n(M’) = 45.
Следовательно, в заданной таблице отсутствуют
три элементарных кода, на которых наша
характеристическая функция оказалась не
доопределенной. Найти эти коды можно путем
последовательного вычитания всех обобщенных
кодов, представляющих заданную таблицу (КДНФ), из
обобщенного кода (- -
- - - ),
представляющего собой множество М в целом. В
результате, в данном случае, получим обобщенный
код К*е = (0 - 0 1 1),
представляющий собой три отсутствующих в таблице 2.25 элементарных кода: (0 0 0 1 1), (0
1 0 1 1) и (0 2 0 1 1). Для определения логического
смысла найденного обобщенного кода достаточно
подставить в него ранее определенные смысловые
значения переменных pi. При этом получим: К*е
= (а = 0)Щ(b = 0)Щ(данные Х введены)Щ(d вычислено).
Другими словами, данный обобщенный код
характеризует ситуацию, когда квадратное
уравнение ay2 + by + c = 0 превращается в
константу c. В этой ситуации, как и в случае,
когда d< 0, можно полагать, что
y = “нет действительных корней”. Поэтому
будем считать, что обобщенный код (0 -
0 1 1) задает условия перехода к действиям Df6,
и дополним таблицу 2.5
соответствующей строкой. В результате получим
корректно и полностью определенную
характеристическую функцию проектируемого
алгоритмического процесса, представленную в
сокращенном виде таблицей 2.26.
Согласно определению функция
F(p21, p32, p23, p24, p25)6, она же F(P)6, представляет собой отображение P® Df множества условий P в множество функциональных действий Df.Рис. 2.7. Схема отображения множества действий – распознавателей (
Dr), реализующих характеристическую функцию F6, в множество действий - преобразователей (Df).
r® Df® Dr, образующих алгоритмический процесс вычисления корней квадратного уравнения ay2+by+c=0
Дальнейшее проектирование типового АП заключается в том, чтобы определить способы и построить частные алгоритмические процессы для реализации действий Dr, вычисляющих значения характеристической функции F(p21, p32, p23, p24, p25)D(f), и действий Dfj, осуществляющих непосредственные преобразования данных x в результаты y. Для построения процесса вычисления значений характеристической функции F(p21, p32, p23, p24, p25)D(f) можно предложить два алгоритма. Первый состоит из следующих простых инструкций:
Данный алгоритм вычисления характеристической функции хорош тем, что он не зависит от конкретного содержания самой функции. Поэтому его можно реализовать как универсальный алгоритм для вычисления любой характеристической функции. Второй алгоритм вычисления значений характеристической функции предписывает последовательное вычисление значений истинности только тех предикатов
pi(t), которые существенно связаны с очередными действиями Dfj. Например, для перехода к выполнению действий из подмножества Df1 в рассматриваемом примере достаточно проверить значение только одного предиката p4. Значения остальных предикатов для условий перехода к Df1 не существенны. Это следует из того, что на месте значений этих предикатов в обобщенном коде, с которым связаны действия Df1, стоят символы “-”. Иначе говоря, для определения условий перехода к действиям Dfj следует проверять значения только тех предикатов pi, которые в соответствующей строке таблицы ХФ содержат символы, отличные от знака тире.Для реализации такого алгоритма вычисления ХФ необходимо ее кодовую ДНФ превратить в эквивалентную ей логическую схему. Эта процедура может быть выполнена формально одним из способов, изложенных в докторской диссертации Устенко А. С.
[14]. Для рассматриваемого примера логическая схема алгоритма вычисления значений ХФ, полученная из таблицы 2.26, показана на рис. 2.9.Рис. 2.9 Логическая схема алгоритма вычисления значений характеристической функции проектируемого АП
2.11.4. Показатели качества алгоритмов и алгоритмических процессов
Обобщенные и частные показателиОбобщенными
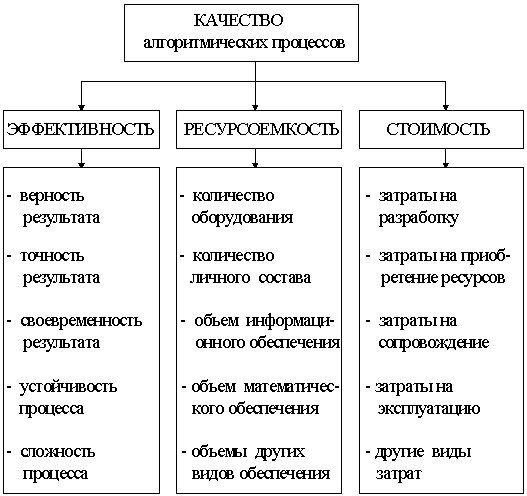
показателями качества алгоритмов и алгоритмических процессов являются характеристики их потребительских свойств:Эти характеристики (показатели) определяются по уже известным нам показателям частных свойств алгоритмов и алгоритмических процессов. Структура функциональных связей между показателями качества алгоритмических процессов и алгоритмов показаны соответственно на рис. 2.10 и рис
. 2.11Рис 2.10. Функциональная структура показателей качества алгоритма
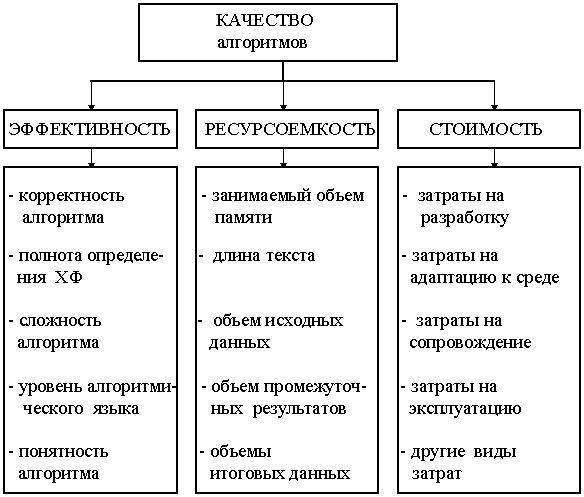
Рис. 2.11. Функциональная структура показателей качества алгоритмических процессов
Из всех перечисленных свойств алгоритмов и алгоритмических процессов наиболее фундаментальным является сложность. Именно сложность оказывает наиболее существенное влияние на ресурсоемкость, стоимость и многие другие показатели качества алгоритмов и алгоритмических процессов. Поэтому при проектировании обычно стремятся из двух алгоритмов или процессов, решающих одну и ту же задачу с одинаковым качеством, выбирать тот из них, который обладает меньшей сложностью. Другими словами, вместо оценки по показателям эффективность - стоимость или эффективность - ресурсоемкость можно использовать показатели эффективность - сложность. Из сказанного следует, что определение и оценка показателей сложности алгоритмов и алгоритмических процессов имеет важное методологическое и практическое значение. Понятие о сложности алгоритмов и алгоритмических процессов имеет несколько различных определений. Чаще всего сложность этих объектов определяется по количеству элементов или частей, из которых они состоят. При этом, например, сложность алгоритмов оценивается по суммарному числу операторов, содержащихся в тексте алгоритма, а сложность алгоритмического процесса - по числу всех действий, выполняемых с момента запуска процесса до получения результата решения задачи. Такая оценка сложности не отражает степени разнообразия множества структурных элементов данного алгоритма или алгоритмического процесса. Поэтому, исходя из определения сложности, как свойства, отражающего разнообразие структурных элементов рассматриваемого объекта, определим показатели сложности для вычисляемых функций (решаемых задач), для алгоритмов и для алгоритмических процессов с учетом специфики оцениваемых объектов.
Показатель сложности решаемой задачи X® YСложность решаемой задачи X® Y определяется степенью неопределенности Н(X® Y) выбора (вычисления) результата решения данной задачи.
Решение задачи X® Y представляет собой процесс выбора элемента
xe из множества Х, e=1,...,m, и выбора соответствующего ему элемента yj из множества Y, j=1,...,N, согласно заданному отображению X® Y. Поэтому источником неопределенности при решении задачи X® Y является разнообразие элементов в множествах X, Y и разнообразие связей в отображении X в Y.В общем случае неопределенность выбора некоторого, безразлично какого именно, элемента
y из множества Y оценивают величиной энтропии:где p(y
j) - вероятность выбора элемента yj из множества Y,N - число всех элементов множества Y,
а - основание логарифма.
Поэтому величина H(Y) может служить мерой разнообразия элементов множества Y. Другими словами, величина H(Y) есть математическое ожидание логарифма вероятности выбора некоторого элемента из Y, безразлично какого именно. Вероятность p(yj) является условной вероятностью, зависящей от вероятности p(xe) выбора элемента xe из множества исходных данных X и от заданного отображения X® Y, согласно которому один и тот же элемент yj может соответствовать нескольким различным наборам исходных данных xe из Х. Поэтому вероятность p(yj) следует вычислять по формуле:
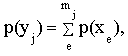где
mj - количество
элементов xe из Х,
которым отвечает элемент yj из Y. Таким образом, приходим к
выводу, что величина неопределенности
(сложность) решения задачи X® Y, с
учетом неопределенности выбора наборов xe исходных данных и заданного
(определенного) отображения X® Y,
может быть вычислена по формуле:
Если вероятности p(x
e) одинаковы для всех xe из Х, то p(xe) = 1/m, где m - количество всех элементов в множестве Х, и формула (2.35) приобретает вид:Выбор показателя 2.34 для оценки сложности функции X® Y основан на следующих соображениях:
Пример. Определим сложность задачи, которую решал известный сказочный герой, стоя на распутье перед камнем с надписью:
“Налево пойдешь - женатым будешь.
Направо пойдешь - коня потеряешь.
Прямо пойдешь - сам погибнешь”.
В данном случае множество Y возможных решений состоит из трех альтернатив: женатым будешь, коня потеряешь, сам погибнешь. Множество X исходных данных также определено тремя условиями: налево пойдешь, направо пойдешь, прямо пойдешь. Между элементами множеств X и Y установлено однозначное соответствие. Поэтому
C(X® Y) = - 3 (1 / 3) loge (1 / 3) = 1,1. Основание логарифма в данном случае принято равным величине e. При первой же попытке формального анализа этой задачи выясняется, что она определена не полностью. В области исходных данных не учтены два возможных условия: “обратно пойдешь” и “на месте останешься”. Этим условиям необходимо сопоставить какие-то следствия yj из Y. Например, по смыслу сказки безрезультатное возвращение домой нашего героя, равно как и безрезультатное сидение на одном месте, свидетельствуют о его несостоятельности. Это, очевидно, и подразумевается в данной сказке “по умолчанию”. Поэтому полностью определенная задача нашего сказочного героя фактически имеет следующую постановку:
“Налево пойдешь - женатым будешь.
Направо пойдешь - коня потеряешь.
Прямо пойдешь - сам погибнешь.
Обратно пойдешь или
на месте останешься - позором покроешься”.
Если наш герой с равной вероятностью может принять любое из пяти перечисленных решений, то сложность получения любого из четырех перечисленных результатов в среднем равна величине:
C(X® Y) = - 3 (1 / 5) loge (1 / 5) - (2 / 5) loge (2 / 5) = 1,3. Следовательно, судя по вычисленным значениям показателя C(X® Y), задача нашего героя на самом деле несколько сложнее, чем ее постановка, изложенная в известной сказке.
Показатель сложности алгоритмаПо определению алгоритм задает процесс вычисления функции X® Y. Для этого в алгоритме имеются описатели
DjОD действий DjОD и описатели (предикаты) PrОP условий PrОP. Здесь символы Dj, D, Pr, P используются для обозначения описателей, соответствующих действий Dj, D и условий Pr, P, r=1,2,...,m , PrОPjНP, j=1,2,...,mj,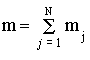
.
Другими словами, алгоритм представляет собой
описание детерминированного отображения P® D, которое по определению
является описанием характеристической функции
типового алгоритмического процесса. Поэтому
сложность алгоритма, задающего этот процесс
можно оценить, как сложность функции P® D по формуле:
В данном выражении величина mj / m есть оценка неопределенности или вероятности выбора подмножества действий Dj из множества D в предположении, что вероятности истинности предикатов Pr одинаковы для всех r=1, 2,...,m, то есть что вероятность p(Pr)=(1/m). В общем случае эти оценки различны для различных подмножеств Dj. Однако, для оценки сложности алгоритма в целом имеет смысл среднее значение (mj / m)* величины (mj/ m), которое можно вычислить следующим способом: m*j=(m/N), (mj / m)* = (m/N/m) = (1/N). При этом сложность алгоритма при условии равных вероятностей выбора действий DjОD оценивается по формуле:
или aC(P® D) = N, или eC(P® D) = N. (2.38)
Последнее уравнение позволяет объяснить смысл введенной нами оценки сложности алгоритмов. В правой части этого уравнения стоит число N описателей
Dj альтернативных действий Dj из множества D. Это прямая оценка разнообразия элементов множества D.Для содержательной интерпретации левой части уравнения 2.39 напомним, что предикаты Pr представляют собой конституенты F(p1, p2,...,pn)Dj характеристической функции F(p1, p2,...,pn)D(f), где p1, p2,...,pn - базовые переменные данной функции (элементарные предикаты, определенные на множестве Х исходных данных и на множестве Z состояний алгоритмического процесса). Число m конституент Pr в множестве P (мощность множества P) определяется по формуле: m = k1- k2- ... - kn, или m = kn, если k1=k2 =... =kn, k - число значений базовой переменной рi, i=1,...,n. Полагая, что основание а логарифма в выражении 2.39 равно числу k значений элементарных предикатов pi, и что величина C(P® D) равна числу n переменных (предикатов pi) в базе характеристической функции алгоритма, приходим к выводу, что kn=N. Это означает, что в алгоритме минимальное разнообразие условий, представленных конституентами Pr должно соответствовать разнообразию описателей действий Dj. При этом сложность алгоритма C(P® D) оценивается числом переменных (элементарных предикатов p), необходимых для корректного задания характеристической функции данного алгоритма. Величина C(P® D) зависит также от значности переменных pi. Поэтому при сравнительной оценке сложности алгоритмов по формуле 2.37 необходимо выбирать единое значение основания логарифма. Рекомендуется принимать a=e (основание натурального логарифма) или а=2 (значность двоичных переменных). В последнем случае сложность алгоритма C(P® D) можно интерпретировать, как среднее число двоичных базовых переменных рi, подлежащих проверке при определении переходов между действиями Dj и Dt, j, t О {1,2,...,N}. Соотношение C(X® Y) / C(P® D) = K (C) является показателем качества проектирования алгоритмов. Чем ближе это отношение к единице, тем проще и, следовательно, лучше спроектирован алгоритм для решения задачи X® Y. Наличие в алгоритмах избыточных описателей условий Pr, переменных pi, или действий Dj усложняет алгоритм и соответственно снижает его качество. Избыточность описателей в алгоритме оправдана только тогда, когда алгоритм реализует дополнительные функции, обеспечивающие устойчивость алгоритмического процесса или необходимые сервисные возможности при решении поставленной задачи.
11.4.4. Оценка сложности иерархических алгоритмовДо сих пор мы рассматривали типовые алгоритмы, с множеством функциональных действий, относящихся к одному уровню иерархии. Схема такого алгоритма показана на рис. 2.12.
Рис 2.12. Схема типового алгоритмического процесса с одним уровнем иерархииОднако на практике чаще всего приходится иметь дело со сложными многоуровневыми иерархическими алгоритмами, в которых подмножества D
j также представлены типовыми алгоритмами, как это показано на рис. 2.13. Оценка сложности таких алгоритмов может быть основана на следующих соображениях. Пусть сложность частного типового алгоритма, задающего подмножество действий Dj равна величине Cj. По определению Cj есть среднее число базовых переменных pi характеристической функции этого алгоритма, проверяемых при определении условных переходов между функциональными действиями в j-том частном алгоритме. Так как на каждом иерархическом уровне сложного алгоритма может быть несколько частных алгоритмов, то имеет смысл оценка Cu средней сложности частных алгоритмов на данном иерархическом уровне.Рис. 2.13. Схема типового алгоритмического процесса с двумя уровнями иерархии
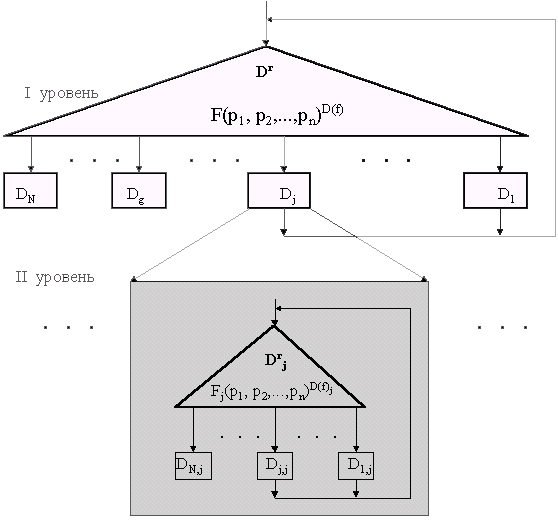
При этом сложность всего сложного иерархического алгоритма в целом оценивается величиной где u - номер иерархического уровня в сложном алгоритме, Cu,r=C(P® D)u,r - сложность r-того частного алгоритма на уровне с номером
u, Nu - количество частных алгоритмов на этом
уровне, r=1,2,...,Nu, C(P® D)
u,r определяется по формулам 2.37 или
2.39 применительно к данному частному
алгоритму. Другими словами, сложность
иерархического алгоритма в целом оценивается
средним числом элементарных условий (базовых
переменных p), проверяемых в процессе реализации
алгоритма. Последовательность проверок условий
p, изображенную на схеме алгоритма, называют
маршрутом. В данной терминологии сложность
алгоритма оценивается средней длиной маршрута
реализации алгоритма от ввода исходных данных до
получения какого-нибудь решения поставленной
задачи.
Пример 1. В разделе 2.11.3 мы рассматривали пример синтеза алгоритма для вычисления корней квадратного уравнения ay
2 + by + c = 0. Суть этого алгоритма состоит в том, что он представляет собой точную инструкцию, как по любому заданному набору xe значений действительных чисел a,b,c получить значение y, удовлетворяющее заданному уравнению. В общем случае область исходных данных X={a,b,c} и область значений корней Y={y} являются бесконечными. Однако многие значения y из Y вычисляются по одним и тем же правилам (формулам Fj(x)), если соответствующие исходные данные xe из X удовлетворяют определенным условиям Pr. Поэтому суть алгоритма состоит в том, чтобы для любого xe определить условия Pr применения соответствующей формулы или действия Fj(xe) = ye. Множества условий Pr и соответствующих им формул Fj(x) конечны и должны быть описаны в алгоритме. Поэтому алгоритм представляет собой описание метода отображения P ® F, и сложность алгоритма можно оценить величиной сложности функционального отображения P ® F. Согласно известному методу вычисления корней квадратного уравнения существует 5 условий Pr, разбивающих множество исходных данных X на 5 характерных подмножеств Xr:P1=(a№0)Щ(d>0), P2=(a№0)Щ(d=0), P3=(a=0)Щ(b№0), P4=(a№0)Щ(d<0) и P5=(a=0)Щ(b=0). В результате многообразие элементов бесконечного множества X преобразуется в многообразие подмножеств Xr, которых всего пять. Каждому подмножеству Xr соответствует определенная формула Fj. В данном случае таких формул всего четыре: F1= (- b +_Цd)/ 2a, F2= b/ 2a, F3= - c/ b и F4- сообщение “действительных корней нет”. В методике предполагается, что формула F4 соответствует условию P4 и условию P5. Поэтому оценка сложности рассматриваемого метода решения поставленной задачи выполняется по формуле:где N - количество альтернативных формул, преобразующих элементы xeОXr в элементы yjОY,
mj=1 для jО{1,2,3} и mj = 2 для j=2,
m = 5 количество условий Pr, разделяющих множество X на подмножества Xr,
а - основание натурального логарифма. При этом C(P®F)=
-(3/5)loga(1/5)-(2/5)loga(2/5)=1,3322. Однако реальный алгоритм, реализующий изложенный метод, должен содержать еще дополнительные условия и описатели функций или действий, предназначенные для организации соответствующего алгоритмического процесса на заданных технических средствах. В данном примере для этой цели были добавлены условия, обеспечивающие ввод исходных данных и вычисление значения детерминанта d. В результате количество условий Pr увеличилось до семи, а число описателей действий Df, реализующих функции Fj(x) и другие действия, увеличилось до шести. Таким образом, реальный алгоритм представляет собой описание отображения P ® Df, которое задается таблицей 2.26. Оценке сложности алгоритма при этом получается в результате следующих вычислений: C(P® Df)= -(5/7)loga(1/7)-(2/7)loga(2/7) =1,7487. Для сравнения оценки сложности математической методики решения задачи и оценки сложности соответствующего ей типового алгоритма введем коэффициент сложности: K(C) = C(P® Df) / C(P® F). (2.41)В данном примере K(C) =1,3126 показывает, что алгоритм сложнее методики, на основании которой он составлен примерно на 30%. Это усложнение происходит за счет необходимости явно описывать в алгоритме все действия, которые в методике выполняются “по умолчанию”.
Пример 2. Примером иерархических алгоритмов является так называемые диалоговые человеко-машинные системы. В них после запуска алгоритмического процесса и прихода его в определенное устойчивое состояние Sg на экране дисплея появляется сообщение в виде меню, в котором пользователю предлагается несколько вариантов дальнейшего продолжения процесса. Действия пользователя также могут состоять из нескольких допустимых вариантов, заранее предусмотренных в алгоритме. Комбинация элементов меню qОQg, значений параметров данного состояния hОHg и действий пользователя rОRg приводит к следующему состоянию St алгоритмического процесса. Каждое такое состояние соответствует определенному уровню сложного иерархического алгоритма и может быть представлено одним типовым алгоритмом. Макет отдельного состояния Sg представлен на рис. 2.14.
Рис. 2.14. Макет одного состояния диалоговогоалгоритмического процесса
Заключительным действием в каждом состоянии Sg является переход в следующее состояние St. В новом состоянии выдается новое меню и так далее. В качестве примера диалогового алгоритма рассмотрим алгоритм, реализующий процесс автоматизированного обучения иностранному языку по словарю. Алгоритм предусматривает два режима обучения. Первый режим заключается в том, что обучаемому показывают на экране N иностранных слов из заданного словаря и русское слово, являющееся переводом одного из показанных иностранных слов. Обучаемому необходимо стрелкой “мышки” указать иностранное слово, соответствующее показанному на экране русскому слову. Факт правильного ответа подтверждается сообщением “правильно” и запоминается в памяти ЭВМ, а обучаемому выдается следующее русское слово из заданного набора. При этом правильно переведенные обучаемым русские слова больше не показывается на экране. Если обучаемым допущена ошибка, то ему сообщается об этом и выдается другое русское слово для опознания, а ранее заданное слово остается для следующего предъявления. После того, как обучаемый правильно укажет перевод всех N заданных слов, первый режим обучения заканчивается сообщением: “Вы усвоили заданные слова. Переходите ко второму режиму обучения”. Второй режим обучения состоит в том, что обучаемому показывают на экране русское слово из заданного словаря, состоящего из тех же N слов, а он должен ввести с клавиатуры соответствующее иностранное слово - перевод. Реакция системы на правильный и неправильный ответ обучаемого такая же, как и в первом режиме обучения. Предварительная описательная характеристическая таблица данного алгоритма представлена в виде таблицы 2.27. В ней описаны четыре состояния алгоритмического процесса: S0, S1, S2, S3,. Каждое состояние St определено на собственной базе предикатов p1, ...,pn(t) и имеет собственную характеристическую функцию Ft, по которой можно определить логическую сложность алгоритма данного состояния. Так для состояния S0 по функции F0 находим:
С(S0) = - (1/4) loga (1/4) - (3/4) loga (3/4) = 0,562.
Для состояний
S1, S2, S3 на основании функций F1, F2, F3 соответственно подучим следующие оценки сложности этих состояний:С(S
1) = - (3/6) loga (1/6) - (3/6) loga (3/6) = 1, 242,С(S
2) = - (2/8) loga (1/8) - (2/8) loga (2/8) - (4/8) loga (4/8) = 1,213,С(S
3) = - (2/8) loga (1/8) - (2/8) loga (2/8) - (4/8) loga (4/8) = 1,213.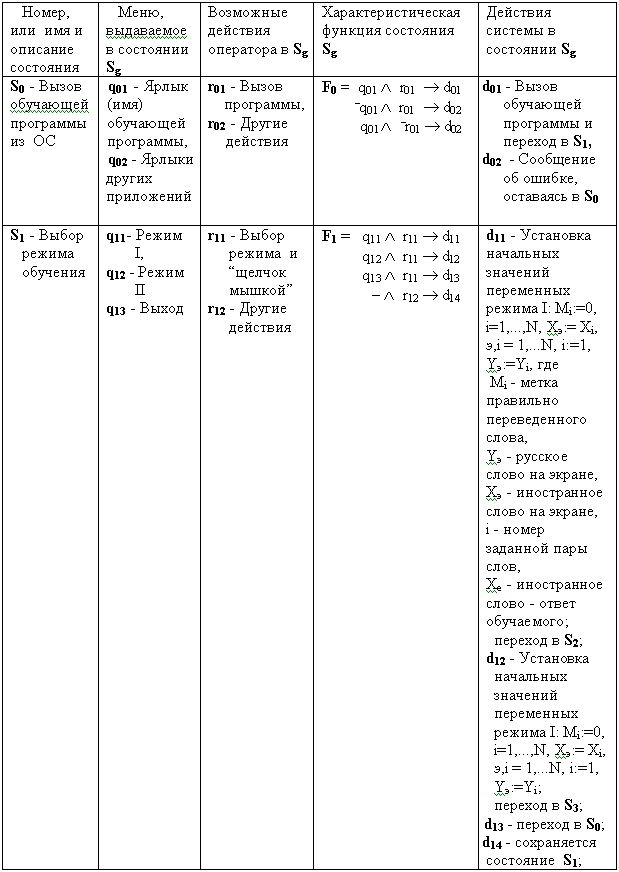
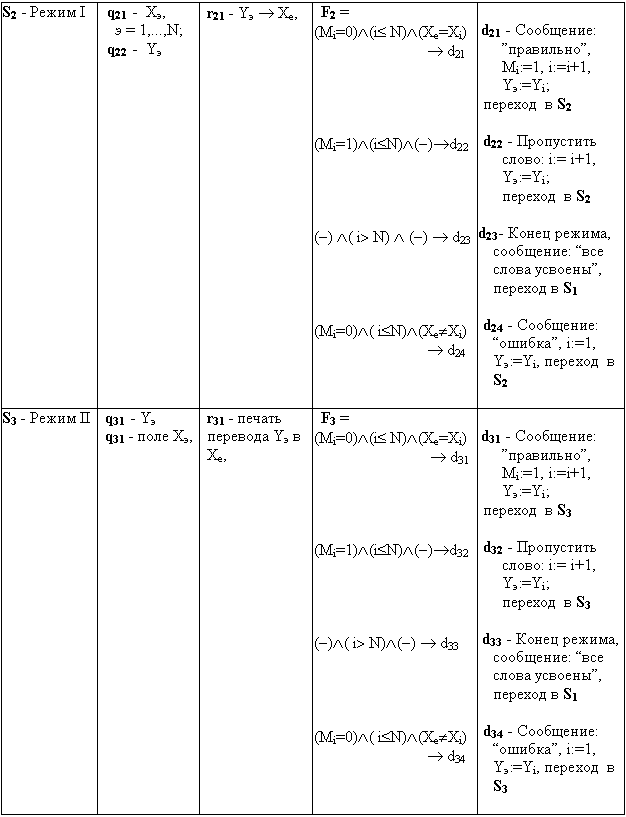
Для получения оценки сложности рассматриваемого обучающего алгоритма в целом желательно предварительно составить наглядную схему его состояний примерно такую, какая показана на рис. 2.15.
Рис. 2.15. Иерархическая схема алгоритма обучения иностранному языку
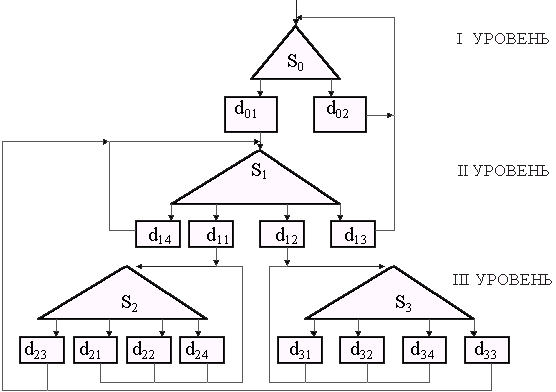
Из данного рисунка видно, что рассматриваемый алгоритм состоит из трех иерархических уровней. Первый и второй уровни алгоритма описывают по одному состоянию алгоритмического процесса, а третий уровень алгоритма описывает два состояния (S2 и S3). Поэтому согласно изложенной выше методике определения сложности типовых иерархических алгоритмов искомая оценка сложности может быть вычислена по следующей формуле: C(P® Df)= C(S0)+C(S1)+[C(S2)+C(S3)]/2 =3,017. Так как алгоритм однозначно задает соответствующий алгоритмический процесс, то сложность алгоритмического процесса можно оценивать сложностью его алгоритма с учетом сложности С(L) преобразования алгоритмического языка L , на котором представлен данный алгоритм, в соответствующую машинную программу.
где K(L) - коэффициент усложнения алгоритма при переводе его на машинный язык.
главная об авторе содержание часть1 часть3 часть4 литература
