1.5. Нечеткие отношения. Проекции
Для практических задач большое значение имеет понятия нечеткого F-отношения.
Пусть X1,X2,
..., Xn -
некоторые множества. Тогда
нечеткое n-арное отношение
Q определяется
как нечеткое подмножество их
декартового произведения X= X1*X2
*...*Xn, т.е.![]()
Например, функция
![]()
определяет
бинарное F-отношение
Q в R
2, т.е. ![]() .
.
Декартовым
произведением F-множеств ![]() ,
называется F-множество
A= A 1*A 2*...*An из F(X) = F(X1*
X2 *...*Xn
) c функцией
принадлежности вида
,
называется F-множество
A= A 1*A 2*...*An из F(X) = F(X1*
X2 *...*Xn
) c функцией
принадлежности вида
![]() . (1.8)
. (1.8)
Распространенными примерами (бинарных) нечетких отношений являются много больше чем, имеет сходство, имеет отношение и т.д. Например, функция принадлежности отношения близко к можно определить следующим образом:
![]()
Пример 1.4. Предположим для примера, что Х={брат, сестра}, Y={отец, мать}, тогда бинарное нечеткое отношение сходстваможно записать в виде:
сходство = 0,8/(б, о) + 0,6/(б, м) + 0,4/(с, о) + 0,9/(с, м).
Данное отношение можно представить также и в виде матрицы отношения:
| отец | мать | |
| брат | 0,8 |
0,6 |
| сестра | 0,4 |
0,9 |
в которой (i,j)-й элемент равен
значению функции ![]() для i-го значения х и j-го значения у.
для i-го значения х и j-го значения у.
Если множества значений переменных конечны, то матрица композиции (произведения) отношений R°S равна максиминному произведению матриц отношений R и S. В максиминном произведении матриц вместо операции сложения и умножения используются операции U и U соответственно. Например,
| 0,3 | 0,8 | 0,5 | 0,9 | 0,4 | 0,8 | ||
| 0,6 | 0,9 | ° | 0,4 | 1 | = | 0,5 | 0,9 |
Например, предположим, что А и F имеют вид:
А = 0,2/1 + 1/2 +0,3/3
F = 0,8(1,1) + 0,9(1,2) + 0,2(1,3) + 0,6(2,1) + 1(2,2) + 0,4(2,3)+ 0,5(3,1) + 0,8(3,2) + 1(3,3).
Выражая А и F с помощью матриц и образуя матричное произведение, получаем
| 0,8 | 0,9 | 0,2 | ||||||||
| 0,2 | 1 | 0,3 | ° | 0,6 | 1 | 0,4 | = | 0,6 | 1 | 0,4 |
| 0,5 | 0,8 | 1 |
Важную роль в ТНМ играет понятие проекции F-отношения. Дадим определение проекции бинарного F-отношения.
Пусть ![]() - функция
принадлежности F-отношения в X
* Y. Проекции QX и QY отношения Q на X и Y - есть множества в X и Y с функцией
принадлежности вида:
- функция
принадлежности F-отношения в X
* Y. Проекции QX и QY отношения Q на X и Y - есть множества в X и Y с функцией
принадлежности вида:
![]() , (1.9)
, (1.9)
![]() . (1.10)
. (1.10)
Пример 1.5. Пусть X=Y=R - числовая прямая и в R2= X* Y задано F-отношение:
![]() .
.
Найдем проекции QX и Qy. Так как ![]() -
дифференцируема по x и по y во всей плоскости, то
для любого фиксированного x из уравнения
-
дифференцируема по x и по y во всей плоскости, то
для любого фиксированного x из уравнения ![]() находим,
что
находим,
что ![]() доставляет
максимум функции
доставляет
максимум функции![]() и, следовательно,
и, следовательно,![]() .
.
Из соображения
симметрии ![]() .
.
Пример 1.6. Пусть на R2 задана функция:
![]() .
.
Определим F-отношение Q в R2 следующим образом:
![]()
Из уравнения ![]() имеем
имеем ![]() и,
следовательно,
и,
следовательно,![]() ,
, ![]()
Из соображения
симметрии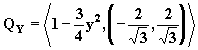 .
.
Условной
проекцией F -отношения Q на X при произвольном
фиксированном ![]() называется множество
называется множество ![]() с
функцией принадлежности вида
с
функцией принадлежности вида![]() . (1.11)
. (1.11)
Аналогично
определяется условная проекция на Y при заданном ![]() :
:
![]() . (1.12)
. (1.12)
Из данного определения видно, что проекции Q X и Qy не влияют на условные проекции P X и Py . соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
Условные проекции второго типа определяются следующим образом:
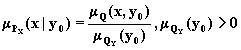 (1.13)
(1.13)
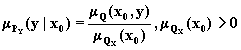 (1.14)
(1.14)
Если ![]() или
или ![]() , то
полагаем, соответственно, что
, то
полагаем, соответственно, что ![]() или
или ![]() .
.
Замечание. Поскольку для всех х и y выполняется
![]() ,
, ![]() , то в выражениях (1.13) и
(1.14)
, то в выражениях (1.13) и
(1.14) ![]() ,
, ![]() .
.
Кроме того, условные проекции первого типа содержатся в соответствующих проекциях второго типа.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]