1.6. Независимость проекций

Пусть X и Y - базовые множества, Q - нечеткое отношение в X*Y и Q_X и Q_y - его проекции на X и Y соответственно.

F-множества Q_X и Q _y называются независимыми, если

Q= Q_X*Q_y.

Следовательно, они независимы по первому типу, если

, (1.15)

и независимы по второму типу, если

(1.16)

В противном случае проекции Q_X и Q_y являются зависимыми (соответствующего типа).

Независимости второго типа можно дать следующую интерпретацию. Соотношения (1.13) и (1.14) с учетом произвольности х₀ и у₀ перепишем в виде

, (1.17)

. (1.18)

Сравнивая (1.17) и (1.18) с (1.16) получаем, что для независимости второго типа необходимо и достаточно выполнение условий:

, ,

где и - F-функции условных проекций второго типа.

Пример 1.7. Пусть X=Y=R и F-отношение в R² определяется функцией:

.

В этом случае

Следовательно, проекции Q_X и Q_y независимы как по первому так и по второму типу. F-функции условных проекций первого типа равны

, ,

а второго типа

, .

Если определить

,

то получим

В этом случае проекции Q_X и Q _y независимы по первому типу, но уже зависимы по второму.F-функции условных проекций второго типа равны

, .

Пример 1.8. Пусть в R ² определено F-отношение:

,

где с ₁, с₂ и с₃ такие, что .

Из уравнения имеем

,

откуда .

Подставляя полученное выражение в , получим

.

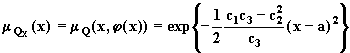По аналогии, для Q_y имеем

,

где .

Для условных проекций второго типа по (1.13) и (1.14) получаем выражения:

,

.

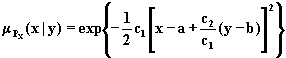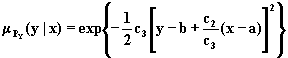Таким образом, если с₂ =0, то Q_X и Q_y независимы по второму типу, поскольку в этом случае

,

и, кроме того, имеем

, .

При с₂ = 0 множества Q _x и Q_y являются зависимы по второму типу.

Если положить, например, с ₁= с₂ =0, то

,

,

и, следовательно,

т.е. проекции Q_X и Q_y являются независимыми по первому типу. Аналогичное утверждение справедливо при с₂= с ₃=0.

Теорема 1.1.Пусть и существуют такие и , что.

Тогда, если , то A и B являются проекциями F -отношения Q.

Доказательство.

Покажем, например, что B = Q _y. Для произвольного фиксированного y₀ имеем:

Равенство A = Q_X доказывается аналогично.

Теорема 1.2. Пусть и существуют такие и , что

.

Тогда, если А и В нормальные F -множества, т.е.

,

то они являются проекциями F -отношения Q.

Доказательство.

Покажем, например, что B = Q _y. Действительно, для произвольного фиксированного y₀ имеем:

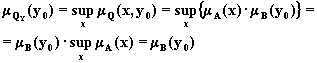
Равенство A = Q_X доказывается аналогично.

Замечание. Из (1.17) и (1.18) выводятся следующие соотношения

,

,

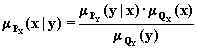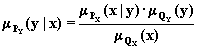аналогичные формулам Байеса в теории вероятности.

Если по аргументам F-функции ясно, на каком базовом множестве она задана и понятен ее смысл, то можно применять более простую форму записи, опуская обозначения F-множеств у соответствующих F -функций (например, ).

[К предыдущей главе].....[К содержанию] ......[К следующей главе]