1.7. Отображение F-множеств
В ТНМ считается,
что произвольное F -отношение в X * Y устанавливает
определенное F-отображение между X
и Y. Пусть в X* Y задано некоторое F-отношение с функцией
принадлежности ![]() , которое можно
толковать как нечеткий график F
-отображения,
вводимого следующим образом.
, которое можно
толковать как нечеткий график F
-отображения,
вводимого следующим образом.
Говорят, что
задано F-отображение
f: X® Y, если каждому A![]() F(X) ставится в
соответствие f(A)
F(X) ставится в
соответствие f(A)![]() F(Y) по следующему правилу
F(Y) по следующему правилу
![]() , (1.19)
, (1.19)
где функция fi определяет какую-либо из операций пересечения i-го типа.
Соотношение (1.19)
для i=1 получено
в работе Заде [98]по
аналогии геометрическому способу
построения образа элемента x![]() X по графику обычного
отображения f:R®
R.
X по графику обычного
отображения f:R®
R.
Процедура построения
множества f(A)
по (1.19) при A![]() F(X)
заключается в следующем. Пусть y
0
F(X)
заключается в следующем. Пусть y
0![]() Y - произвольный
фиксированный элемент. Тогда
Y - произвольный
фиксированный элемент. Тогда ![]() есть F-функция
есть F-функция ![]() условной
проекции первого типа P
условной
проекции первого типа P![]() F(X). Следовательно,
выражение
F(X). Следовательно,
выражение ![]() является F-функцией множества
является F-функцией множества ![]() P и величина
P и величина ![]() равна
супремуму этой функции на X.
равна
супремуму этой функции на X.
Таким образом,
функция ![]() является результатом
решения параметрической
экстремальной задачи, в
которой в качестве параметра
выступает переменная y.
является результатом
решения параметрической
экстремальной задачи, в
которой в качестве параметра
выступает переменная y.
В частности, если f есть отношение в X*Y, определяющее обычное отображение f:X®Y, т.е.
![]() и
и
![]() ,
,
то из (1.19) для i=1 ,2,4 следует, что
![]() , (1.20)
, (1.20)
а для i=3
![]() .
.
Пример 1.9. Пусть X=Y=R и f:R ® R определяется следующим F -отношением:
![]() .
.
Если
![]() ,
,
то для i=1 максимум функции ![]() по x при произвольном
фиксированном y достигается в точке
по x при произвольном
фиксированном y достигается в точке ![]() ,
определяемой из уравнения
,
определяемой из уравнения
![]() ,
,
решение которого дает
![]() .
.
Подставляя ![]() в
в ![]() или в
или в ![]() получим
получим
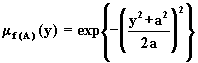
Если a=0, т.е. ![]() , то очевидно, что
, то очевидно, что ![]() определяется
из уравнения
определяется
из уравнения
![]()
т.е. ![]() и,
следовательно,
и,
следовательно,
![]() .
.
Если i=2, т.е. операция пересечения определяется по второму типу, то из уравнения
![]()
находим, что ![]() и,
следовательно,
и,
следовательно,
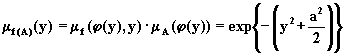
Пример 1.10. Пусть снова X=Y=R и задано отображение y=f(x)=x2. Если
![]() ,
,
то учитывая, что ![]() имеем
имеем
![]()
![]()
Следовательно, согласно (8.2)
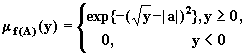
В том случае,
когда A и
f - конечные F-множества, т.е. ![]() и
и ![]() представимы
в виде вектора и матрицы, то,
например, для i=1,
т.е.
представимы
в виде вектора и матрицы, то,
например, для i=1,
т.е. ![]() ,
нахождение f(A) сводится максиминному
произведению вектора на матрицу.
В этой операции
произведение значений F-функций
заменяется взятием их минимума, а
сумма - их максимумом.
,
нахождение f(A) сводится максиминному
произведению вектора на матрицу.
В этой операции
произведение значений F-функций
заменяется взятием их минимума, а
сумма - их максимумом.
Поясним это следующим примером.
Пример 1.11.
Пусть ![]() ,
,
![]() ,
,
 .
.
Слева от
наклонной черты указывается
значение F-функций
в соответствующей точке.
Перемножая ![]() и
и ![]() по описанному правилу,
получим
по описанному правилу,
получим
![]() .
.
Этот же результат
можно получит другим путем, заметив
из (1.19) следующий факт. Если x - произвольный
фиксированный элемент из X , то F -функция ![]() определяет
в F(Y)
некоторое множество f(A(x)). Тогда
определяет
в F(Y)
некоторое множество f(A(x)). Тогда
![]() . (1.21)
. (1.21)
Для нашего примера имеем
![]() ,
,
![]() ,
,
![]() ,
,
откуда
![]() .
.
Исходя из (1.19)-(1.21), Л. Заде сформулировал так называемый принцип обобщения, который для нечетких множеств представляет собой основное равенство, позволяющее расширить область определения Хотображения или отношения F, включив в нее наряду с точками произвольные нечеткие подмножества Х. Предположим, что А - нечеткое подмножество вида
![]() .
.
Тогда принцип обобщения утверждает, что
![]() , (1.22)
, (1.22)
т.е. образ
множества А при отображении А
можно получить зная образы
элементов ![]() при этом отображении.
при этом отображении.
Во многих
приложениях принципа обобщения
возникает следующая проблема.
Имеется функция n переменных ![]() и
нечеткое множество (отношение) А в
и
нечеткое множество (отношение) А в
![]() ,
характеризующееся функцией
принадлежности
,
характеризующееся функцией
принадлежности ![]() . Однако во многих
случаях известно не само множество А,
а его проекции
. Однако во многих
случаях известно не само множество А,
а его проекции ![]() на
на ![]() соответственно. В
связи с этим возникает вопрос:
какое выражение следует
использовать для
соответственно. В
связи с этим возникает вопрос:
какое выражение следует
использовать для ![]() .
.
В таких случаях
обычно, если нет специально
оговоренных ограничений на
переменные ![]() , предполагают, что функция
принадлежности отношения А
имеет вид
, предполагают, что функция
принадлежности отношения А
имеет вид
![]() , (1.23)
, (1.23)
где ![]() , i=1,...,n-
функция
принадлежности множества Аi, что эквивалентно
предположению о том, что А -
декартово произведение своих
проекций., т.е.
, i=1,...,n-
функция
принадлежности множества Аi, что эквивалентно
предположению о том, что А -
декартово произведение своих
проекций., т.е.
![]() .
.
Пример 1.12. Пусть F- арифметическое произведение X1и X 2 , а проекции А 1 и А2 определены следующим образом:
А 1= примерно 2 = 0,6/1 + 1/2 + 0,8/3,
А 2= примерно 6 = 0,8/5 + 1/6 + 0,7/7.
Используя (1.23) и применяя принцип обобщения, имеем:
| 0,8/5 | 1/6 | 0,7/7 | |
| 0,6/1 | 0,6/5 | 0,6/6 | 0,6/7 |
| 1/2 | 0,8/10 | 1/12 | 0,7/14 |
| 0,8/3 | 0,8/15 | 0,8/18 | 0,7/21 |
Таким образом, арифметическое произведение нечетких чисел примерно 2 и примерно 6 есть нечеткое число с найденной функцией принадлежности.
Понятие отображение F-множеств играет исключительно важную роль как в практических приложениях, так и при введении алгебраических операций над нечеткими величинами.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]