называется
дискретной, если множество 
конечное
или счетное. Если мощность 
равна
континууму, то величина А
называется непрерывной.2.1. Математическая структура базового множества и свойство выпуклости
В предыдущей главе у базового множества Х не предполагалось наличие какой-либо внутренней математической структуры. Если считать, например, что Х - векторное, топологическое, метрическое или какое-либо другое пространство, то естественно возникает вопрос, каким образом определенную структуру базового множества можно распространить на класс F(X) ?
Будем полагать, X=R - множество вещественных чисел, а элементы класса F(R) будем называть нечеткими величинами. Основные задачи, решаемые в данной главе, заключаются в следующем:
1. Распространить алгебраические операции из R на класс F(R).
2. Исследовать свойства полученных операций.
3. Показать некоторые аналитические и численные методы нахождения результатов алгебраических операций над F-величинами.
Величина называется
дискретной, если множество конечное
или счетное. Если мощность равна
континууму, то величина А
называется непрерывной.
Поскольку некоторые пункты исследования тесно связаны с методами решения экстремальных задач, то основное внимание будем уделять непрерывным F-величинам. Кроме того, среди всех непрерывных F-величин целесообразно выделить следующие.
Величина А
F(R) называется выпуклой
, если для любых 
и любого g [0,1]
справедливо неравенство
(2.1)
Если в (2.1) равенство возможно только при g =0 и g =1, то величина A называется строго выпуклой.
Пример 2.1.
Пусть АF(R) и
имеет F-функцию
вида
или
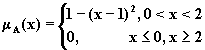
Очевидно, что в обоих случаях А - строго выпуклая F-величина.
Пример 2.2. Пусть АF(R) определяется
следующим образом:
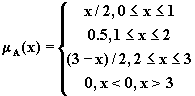
График функции 
показан
на рис.2.1.
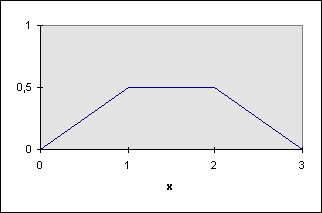
Рис.2.1.
График функции для примера 2.2.
Если 
, то для
любого g [0,1] имеем 
,
т.е. А - выпуклая F-величина, поскольку
для всех остальных 
выполняется
неравенство
.
Нетрудно
заметить, что если А - строго
выпуклая F-величина,
то функция на 
- строго возрастающая или
строго убывающая; или строго
возрастает до некоторого 
, а затем
строго убывает.
Если А -
выпуклая, то 
может дополнительно иметь
участки, где постоянная.
Связь между выпуклыми величинами и их a -уровневыми множествами из R устанавливается следующей теоремой.
Теорема 2.1.
Величина АF(R) выпукла тогда и только
тогда, когда множества 
выпуклы
для всех 
.
Доказательство.
Пусть величина А F(R) - выпуклая. Рассмотрим a-уровневое
множество
.
Если 
пусто, то
оно выпукло. Пусть 
, т.е. 
и 
. Тогда из условия
выпуклости для A получим
.
В силу того, что 
следует,
что при любом 
точка 
принадлежит 
, т.е. оно выпукло в R
.
С другой стороны,
предположим, что множества 
выпуклы
в R при любом
. Пусть
и 
.
Необходимо доказать, что для 
.
Предположим
противное, т.е. пусть найдется 
такое,
что
.
Тогда очевидно,
что для любого 
, 
, точки 
.
Следовательно, поскольку по
условию теоремы множество 
-
выпуклое, то 
должна принадлежать 
, что не
выполняется, т.к. 
. Полученное
противоречие завершает
доказательство.
Аналогичную теорему можно доказать и для слабых a-уровневых множеств.
Следствие.
Учитывая тот очевидный факт, что
если А ,BF(R) - выпуклые
и при этом 
выпуклое при любом 
заключаем,
что 
-
выпуклая F -величина.
Множество
называется
выпуклым, если для любых
точек 
и 
из 
и любого 
выполняется неравенство
(2.2)
Если равенство в (2.2) возможно только при g=0 и g=1, то Q называется строго выпуклым.
Теорема 2.2.
Если А,BF(R)- выпуклые,
то 
-
выпуклое.
Доказательство.
Действительно, если 
, то 
В этом случае, учитывая второе и третье определения, имеем
что и доказывает теорему.
Теорема 2.3.
Если 
- выпуклое,
то его проекции являются выпуклыми.
Доказательство
. Пусть 
, F-функция
одной из проекций и точки 
и 
такие,
что 
и 
.
Тогда для
произвольного 
имеем:
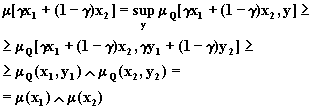
Выпуклость второй проекции доказывается аналогично.
F-отображение f: R® R называется выпуклым, если соответствующее ему F-отношение выпукло в R2.
Теорема 2.4.
Если f: R® R выпуклое отображение
и АF(R) выпуклая величина, то f(A) тоже будет выпуклой.
Доказательство. Величина f(A) имеет F -функцию
Пусть 
и 
такие,
что
.
Тогда для
произвольного 
имеем:
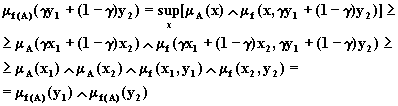
Следствие.
Если АF(R)
выпуклая величина и f: R® R линейная функция, то f(A) - выпуклая.
Пример 2.3.
Пусть 
и 
. В
силу взаимной однозначности
отображения f из
(1.20) имеем
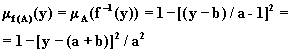
Пример 2.4.Пусть
и 
, т.е. f - нелинейное
отображение. В этом случае получим
,
и, следовательно, 
, т.е. не
является выпуклой.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]