3.3. Решение систем уравнений с нечеткими и интервальными коэффициентами
В работе [2] отмечается значительное преимущество нечетких алгоритмов для систем линейных уравнений в сравнении со случаями, когда коэффициенты и правые части уравнений заданы случайными величинами.
Используя
введенную в главе 2 нечеткую
арифметику, казалось бы достаточно
просто решать такую систему
обычными методами, например,
методом Гаусса и т.д. Однако
нечеткий вектор 
результатов в этом
случае оказывается сильно
"размытым"; из-за наличия
операций деления все время имеется
опасность деления на ноль и имеется
теоретическая некорректность
такого подхода к решению системы
линейных уравнений из-за того, что
множество нечетких чисел не
является группой относительно
операции умножения [2].
Введенные в работах [2, 266, 267, 268] множества нечетких LR и LL-чисел замкнуты (в смысле приближенных формул для умножения и деления) относительно арифметических операций. "Размытость" результата в этом случае значительно уменьшается, однако возникает необходимость проверок правильности пользования приближенными формулами путем анализа ошибок [2]. В этом случае система нечетких линейных уравнений сводится к линейной системе из 3n уравнений с 3n неизвестными с использованием определения равенства для нечетких LR-чисел (два нечетких LR-числа равны, если равны значения всех трех параметров, характеризующих нечеткие числа) [2]. Полученную систему уравнений в целях повышения устойчивости можно свести к задаче нелинейного программирования путем введения функционала от невязок параметров, характеризующих нечеткие числа левых и правых частей уравнений системы [2].
Системы нечетких
уравнений могут быть сведены к
системам обычных
детерминированных уравнений
различными способами [166]. Например, единичный
интервал разбивается на 
r-уровней и каждое
уравнение заменяется
интервальными уравнениями, а затем,
следуя Сойстеру, задача с
ограничениями по включению
преобразуется в задачу с
ограничениями типа неравенств.
Применение этого преобразования
увеличивает размерность задачи,
однако при этом сохраняется
возможность использования хорошо
известных классических методов.
Для решения систем линейных уравнений с нечеткими переменными и вещественными коэффициентами полезно использовать результаты следующей теоремы [38].
Теорема 3.13.
Пусть 
-
базовое множество. 
- обратимая матрица 
и задано
отображение 
вида 
. Тогда, если 
, то справедливо
следующее соотношение
,
(3.50)
,
где 
-
проекция F-вектора
на
ось j.
Доказательство.
Поскольку f -
взаимнооднозначное отображение, то
. По
определению проекции имеем
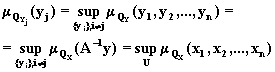
Следствие. Если
,
где 
-
проекция F-вектора
, то из
(3.50 ) и (2.3.) следует, что
.
Рассмотрим систему линейных уравнений с интервальными коэффициентами:
Для решения данной системы уравнений можно использовать, например, следующий итерационный алгоритм.
1. Выбирается
расширенный вектор 
, который
можно представить в виде
2. Вычисляется расширенный вектор свободных членов
(3.51)
3. Исключая
из (3.51),
получаем систему обыкновенных
линейных уравнений относительно
приращений 
, которая решается одним из
известных способов (например,
методом исключения).
4. Определяется
уточненный вектор 
.
5. Снова вычисляется расширенный вектор свободных членов
.
6. Проверяется критерий окончания счета
,
где x - заданная точность.
7. Если условие 6 выполняется, то расчет заканчивается, иначе переходят к этапу 3.
Для решения системы нелинейных уравнений может использоваться также итерационный метод с линеаризацией уравнений на каждом шаге итерации по одному из известных способов (например, методом Ньютона).
1. Вначале систему нелинейных уравнений с помощью введенных операций над сопряженными интервалами приводят к виду
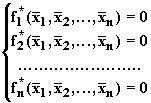
2. Затем на каждом шаге итерации s решается система линейных уравнений
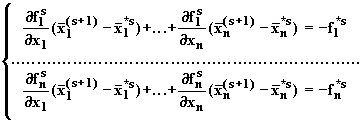
3. Проверяется критерий окончаниния счета
,
где x - заданная точность.
4. Если условие 3 выполняется, то расчет заканчивается, иначе переходят к этапу 2.
Для систем уравнений с нечеткими коэффициентами - производится дискретизации исходных функций принадлежности по r -уровням и решаются соответствующие системы уравнений с интервальными коэффициентами.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]