3.2. Особенности решения нечетких и интервальных уравнений
Многие расчетные и оптимизационные задачи в условиях неопределенности приводят к необходимости решения уравнений с нечеткими или интервальными коэффициентами и переменными. К особенностям нечеткой и интервальной алгебры следует отнести нарушение закона дистрибутивности
![]()
и кроме
того ![]() .
.
Эти особенности создают значительные трудности при решении F -уравнений, поскольку их нельзя упростить путем эквивалентных преобразований. В ряде работ предлагаются методы частичного решения этой проблемы: "дополнительные" операции в [7], использование квазилинейного пространства [247], мнимые интервалы [243], нестандартные вычитание и деление [109], обобщенная и сегментная интервальные арифметики [109].
Одним из возможных путей решения этой проблемы является введение понятия мнимого интервала. В силу следствия теоремы 2.8 все определения вводятся для интервалов вещественной оси, т.е. для пространства I(R) с интервальными операциями.
Если интервал ![]() , то сопряженным
интервалом по отношению к
, то сопряженным
интервалом по отношению к ![]() называют мнимый интервал
называют мнимый интервал![]() .
Множество мнимых интервалов
обозначим через I*(R). Для перехода
.
Множество мнимых интервалов
обозначим через I*(R). Для перехода ![]() к
сопряженному интервалу
справедливы следующие соотношения:
к
сопряженному интервалу
справедливы следующие соотношения:
![]()
![]()
Алгебраические
операции над сопряженными
интервалами определяются
следующим образом [243]. Если ![]() то, согласно (2.76):
то, согласно (2.76):
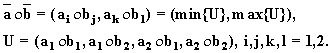
Тогда для
сопряженных интервалов ![]() ,
, ![]() вводятся следующие
соотношения:
вводятся следующие
соотношения:
![]() ,
,![]() ,
,![]()
Например, если ![]() , то
, то ![]() .
Следовательно,
.
Следовательно, ![]() , и
, и ![]() .
.
С использованием
введенных понятий решение
линейного уравнения![]()
записывается в
виде ![]() .
Для уравнения
.
Для уравнения![]() получаем
получаем ![]() .
.
Решениями таких уравнений могут быть и мнимые интервальные величины. В общем случае решение линейного уравнения
![]() (3.49)
(3.49)
имеет вид ![]() .
.
Можно также
показать, что если![]() , то при замене
нескольких или всех
, то при замене
нескольких или всех ![]() полученный результат
полученный результат ![]() .
.
Рассмотрим следующее обобщение для решения нечетких уравнений с использованием понятий сопряженного интервала и интервально-значного нечеткого множества.
Интервально-значное нечеткое множество (i-v нечеткое множество) А, определенное на множестве Х, задается в виде [281]:
![]() ,
,
![]()
Интервально-значную функцию принадлежности можно записать в виде
![]() .
.
Пример
интервально-значной функции
принадлежности приведен на рис. 3.4.
Различные операции с i-v нечеткими
множествами могут выполняться
аналогично соответствующим
операциям нечетких множеств для
нижних ![]() и верхних
и верхних ![]() граничных функций
принадлежности [149].
граничных функций
принадлежности [149].
Обобщение для
решения нечетких линейных
уравнений типа (3.49) состоит в том,
что для каждого r -уровня исходных F-функций находится
интервальное решение ![]() с
помощью обычной интервальной
арифметики и решение
с
помощью обычной интервальной
арифметики и решение ![]() с
использованием сопряженных
интервалов. Таким образом, решение
нечеткого уравнения получаем в
виде интервально-значной функции
принадлежности
с
использованием сопряженных
интервалов. Таким образом, решение
нечеткого уравнения получаем в
виде интервально-значной функции
принадлежности ![]() .
.
Пример 3.11.
Рассмотрим решение уравнения ![]() . Пусть
коэффициенты уравнения заданы
треугольными F-функциями (рис. 3.3).
. Пусть
коэффициенты уравнения заданы
треугольными F-функциями (рис. 3.3).
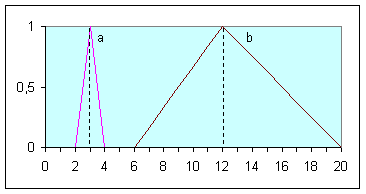
Рис 3.3.
Для носителей
исходных F-множеств
![]() ,
, ![]() находим интервальное
решение
находим интервальное
решение
![]()
с помощью обычной интервальной арифметики и решение
![]()
с использованием сопряженных интервалов.
Аналогично
поступаем для каждого r -уровня исходных F-функций. В результате
получаем интервально-значную
функцию принадлежности ![]() (рис. 3.4).
(рис. 3.4).
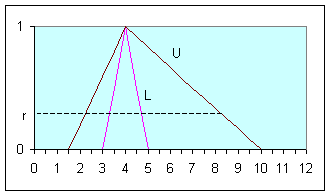
Рис 3.4.
Используя
отношение порядка на множестве ![]() [109], можно сказать, что
для произвольного r-уровня соотношение
[109], можно сказать, что
для произвольного r-уровня соотношение ![]() дает
четкое множество в виде интервала
дает
четкое множество в виде интервала ![]() ,
определяемого функцией
,
определяемого функцией ![]() . С
другой стороны, функция
. С
другой стороны, функция ![]() определяет для выбранного r -уровня расширенный
интервал
определяет для выбранного r -уровня расширенный
интервал ![]() .
.
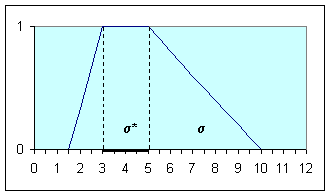
Рис 3.5.
Вводя далее
линейное предпочтение для
элементов ![]() , не включенных в
, не включенных в ![]() , можно
интерпретировать r -уровневое множество
для интервально-значной функции
принадлежности
, можно
интерпретировать r -уровневое множество
для интервально-значной функции
принадлежности ![]() в виде нечеткого
множества первого типа. Пример
такого множества для носителей
в виде нечеткого
множества первого типа. Пример
такого множества для носителей ![]() представлен на рис. 3.5.
представлен на рис. 3.5.
Подобная интерпретация решения нечетких и интервальных уравнений позволяет более адекватно учитывать имеющуюся неопределенность постановки задачи физический смысл исследуемой модели.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]