Основные статистики и таблицы
Описательные статистики
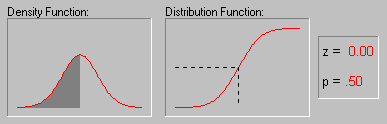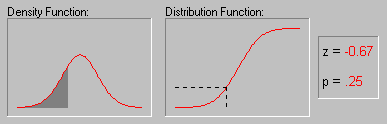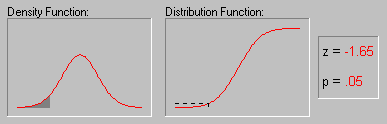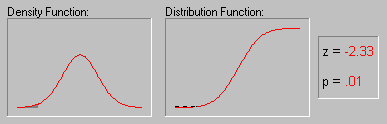
"Истинное" среднее и доверительный интервал. Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее. Среднее - очень информативная мера "центрального положения" наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее. Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия (см. Элементарные понятия статистики), находится "истинное" (неизвестное) среднее популяции. Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции. Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он "накрывает" неизвестное среднее популяции, и наоборот. Хорошо известно, например, что чем "неопределенней" прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки (см. также Элементарные понятия статистики). Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.
Форма распределения; нормальность. Важным способом "описания" переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем. Обычно исследователя интересует, насколько точно распределение можно аппроксимировать нормальным (см. ниже картинку с примером такого распределения) (см. также Элементарные понятия статистики). Простые описательные статистики дают об этом некоторую информацию. Например, если асимметрия (показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. Далее, если эксцесс (показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.

Более точную информацию о форме распределения можно получить с помощью критериев нормальности (например, критерия Колмогорова-Смирнова или W критерия Шапиро-Уилка). Однако ни один из этих критериев не может заменить визуальную проверку с помощью гистограммы (графика, показывающего частоту попаданий значений переменной в отдельные интервалы).
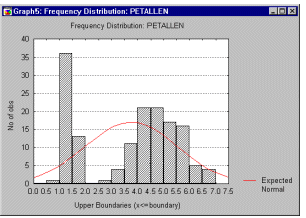
Гистограмма позволяет "на глаз" оценить
нормальность эмпирического распределения. На гистограмму
также накладывается кривая нормального
распределения. Гистограмма позволяет качественно
оценить различные характеристики распределения.
Например, на ней можно увидеть, что распределение
бимодально (имеет 2 пика). Это может быть вызвано,
например, тем, что выборка неоднородна, возможно,
извлечена из двух разных популяций, каждая из
которых более или менее нормальна. В таких
ситуациях, чтобы понять природу наблюдаемых
переменных, можно попытаться найти качественный
способ разделения выборки на две части.
| В начало |
Корреляции
Определение корреляции. Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.
Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.
Простая линейная корреляция (Пирсона r). Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале (см. Элементарные понятия статистики). Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).
Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.
Как интерпретировать значения корреляций. Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r2) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и ее значимость.
Значимость корреляций. Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Как объяснялось выше (см. Элементарные понятия статистики), значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие. Тем не менее, имеется несколько серьезных опасностей, о которых следует знать, для этого см. следующие разделы.
Выбросы. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.
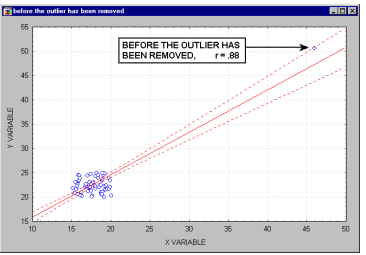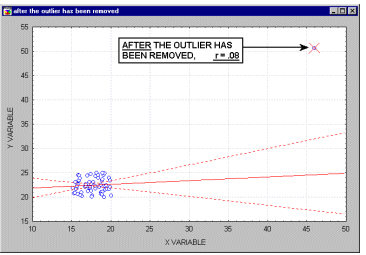
Заметим ,что если размер выборки относительно мал, то добавление или исключение некоторых данных (которые, возможно, не являются "выбросами", как в предыдущем примере) способно оказать существенное влияние на прямую регресии (и коэффициент корреляции). Это показано в следующем примере, где мы назвали исключенные точки "выбросами"; хотя, возможно, они являются не выбросами, а экстремальными значениями.

Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. К сожалению, не существует общепринятого метода автоматического удаления выбросов (тем не менее, см. следующий раздел). Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяния каждый важный случай значимой корреляции. Очевидно, выбросы могут не только искусственно увеличить значение коэффициента корреляции, но также реально уменьшить существующую корреляцию.
См. также Доверительный эллипс.
Количественный подход к выбросам. Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 стандартных отклонений (и даже ±1.5 стандартных отклонений) вокруг выборочного среднего. В ряде случаев такая "чистка" данных абсолютно необходима. Например, при изучении реакции в когнитивной психологии, даже если почти все значения экспериментальных данных лежат в диапазоне 300-700 миллисекунд, то несколько "странных времен реакции" 10-15 секунд совершенно меняют общую картину. К сожалению, в общем случае, определение выбросов субъективно, и решение должно приниматься индивидуально в каждом эксперименте (с учетом особенностей эксперимента или "сложившейся практики" в данной области). Следует заметить, что в некоторых случаях относительная частота выбросов к численности групп может быть исследована и разумно проинтерпретирована с точки зрения самой организации эксперимента. См. также Доверительный эллипс.
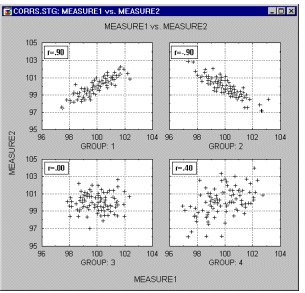
Корреляции в неоднородных группах. Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Представьте ситуацию, когда коэффициент корреляции вычислен по данным, которые поступили из двух различных экспериментальных групп, что, однако, было проигнорировано при вычислениях. Далее, пусть действия экспериментатора в одной из групп увеличивают значения обеих коррелированных величин, и ,таким образом, данные каждой группы сильно различаются на диаграмме рассеяния (как показано ниже на графике).
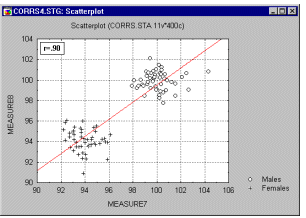
В подобных ситуациях высокая корреляция может быть следствием разбиения данных на две группы, а вовсе не отражать "истинную" зависимость между двумя переменными, которая может практически отсутствовать (это можно заметить, взглянув на каждую группу отдельно, см. следующий график).
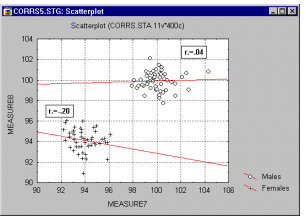
Если вы допускаете такое явление и знаете, как определить "подмножества" данных, попытайтесь вычислить корреляции отдельно для каждого множества. Если вам неясно, как определить подмножества, попытайтесь применить многомерные методы разведочного анализа (например, Кластерный анализ).
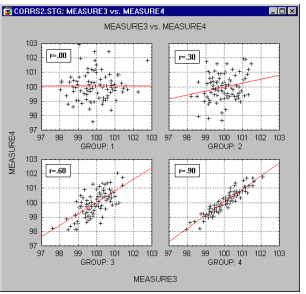
Нелинейные зависимости между переменными. Другим возможным источником трудностей, связанным с линейной корреляцией Пирсона r, является форма зависимости. Корреляция Пирсона r хорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрения диаграммы рассеяния для каждого коэффициента корреляции, является нелинейность. Например, следующий график показывает сильную корреляцию между двумя переменными, которую невозможно хорошо описать с помощью линейной функции.
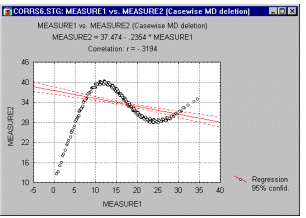
Измерение нелинейных зависимостей. Что делать, если корреляция сильная, однако зависимость явно нелинейная? К сожалению, не существует простого ответа на данный вопрос, так как не имеется естественного обобщения коэффициента корреляции Пирсона r на случай нелинейных зависимостей. Однако, если кривая монотонна (монотонно возрастает или, напротив, монотонно убывает), то можно преобразовать одну или обе переменные, чтобы сделать зависимость линейной, а затем уже вычислить корреляцию между преобразованными величинами. Для этого часто используется логарифмическое преобразование. Другой подход состоит в использовании непараметрической корреляции (например, корреляции Спирмена, см. раздел Непараметрическая статистика и подгонка распределения). Иногда этот метод приводит к успеху, хотя непараметрические корреляции чувствительны только к упорядоченным значениям переменных, например, по определению, они пренебрегают монотонными преобразованиями данных. К сожалению, два самых точных метода исследования нелинейных зависимостей непросты и требуют хорошего навыка "экспериментирования" с данными. Эти методы состоят в следующем:
Разведочный анализ корреляционных матриц. Во многих исследованиях первый шаг анализа состоит в вычислении корреляционной матрицы всех переменных и проверке значимых (ожидаемых и неожиданных) корреляций. После того как это сделано, следует понять общую природу обнаруженной статистической значимости (см. Элементарные понятия статистики). Иными словами, понять, почему одни коэффициенты корреляции значимы, а другие нет. Однако следует иметь в виду, если используется несколько критериев, значимые результаты могут появляться "удивительно часто", и это будет происходить чисто случайным образом. Например, коэффициент, значимый на уровне .05, будет встречаться чисто случайно один раз в каждом из 20 подвергнутых исследованию коэффициентов. Нет способа автоматически выделить "истинную" корреляцию. Поэтому следует подходить с осторожностью ко всем не предсказанным или заранее не запланированным результатам и попытаться соотнести их с другими (надежными) результатами. В конечном счете, самый убедительный способ проверки состоит в проведении повторного экспериментального исследования. Такое положение является общим для всех методов анализа, использующих "множественные сравнения и статистическую значимость". Эта проблема также обсуждается в описании процедур Апостериорные сравнения средних и Группировка.
Построчное удаление пропущенных данных в сравнении с попарным удалением. Принятый по умолчанию способ удаления пропущенных данных при вычислении корреляционной матрицы - состоит в построчном удалении наблюдений с пропусками (удаляется вся строка, в которой имеется хотя бы одно пропущенное значение). Этот способ приводит к "правильной" корреляционной матрице в том смысле, что все коэффициенты вычислены по одному и тому же множеству наблюдений. Однако если пропущенные значения распределены случайным образом в переменных, то данный метод может привести к тому, что в рассматриваемом множестве данных не останется ни одного неисключенного наблюдения (в каждой строке наблюдений встретится, по крайней мере, одно пропущенное значение). Чтобы избежать подобной ситуации, используют другой способ, называемый попарным удалением. В этом способе учитываются только пропуски в каждой выбранной паре переменных и игнорируются пропуски в других переменных. Корреляция между парой переменных вычисляется по наблюдениям, где нет пропусков. Во многих ситуациях, особенно когда число пропусков относительно мало, скажем 10%, и пропуски распределены достаточно хаотично, этот метод не приводит к серьезным ошибкам. Однако, иногда это не так.
Например, в систематическом смещении (сдвиге) оценки может "скрываться" систематическое расположение пропусков, являющееся причиной различия коэффициентов корреляции, построенных по разным подмножествам. Другая проблема связанная с корреляционной матрицей, вычисленной при попарном удалении пропусков, возникает при использовании этой матрицы в других видах анализа (например, Множественная регрессия, Факторный анализ или Кластерный анализ). В них предполагается, что используется "правильная" корреляционная матрица с определенным уровнем состоятельности и "соответствия" различных коэффициентов. Использование матрицы с "плохими" (смещенными) оценками приводит к тому, что программа либо не в состоянии анализировать такую матрицу, либо результаты будут ошибочными. Поэтому, если применяется попарный метод исключения пропущенных данных, необходимо проверить, имеются или нет систематические закономерности в распределении пропусков.
Как определить смещения, вызванные попарным удалением пропущенных данных. Если попарное исключение пропущенных данных не приводит к какому-либо систематическому сдвигу в оценках, то все эти статистики будут похожи на аналогичные статистики, вычисленные при построчном способе удаления пропусков. Если наблюдается значительное различие, то есть основание предполагать наличие сдвига в оценках. Например, если среднее (или стандартное отклонение) значений переменной A, которое использовалось при вычислении ее корреляции с переменной B, много меньше среднего (или стандартного отклонения) тех же значений переменной A, которые использовались при вычислении ее корреляции с переменной C, то имеются все основания ожидать, что эти две корреляции (A-B и A-C) основаны на разных подмножествах данных, и, таким образом, в оценках корреляций имеется сдвиг, вызванный неслучайным расположением пропусков в значениях переменных.
Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения. Другим общим методом, позволяющим избежать потери наблюдений при построчном способе удаления наблюдений с пропусками, является замена средним (для каждой переменной пропущенные значения заменяются средним значением этой переменной). Подстановка среднего вместо пропусков имеет свои преимущества и недостатки в сравнении с попарным способом удаления пропусков. Основное преимущество в том, что он дает состоятельные оценки, однако имеет следующие недостатки:
Ложные корреляции. Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными (см. Элементарные понятия статистики), однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями "других", остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причиненный ущерб, так и на число вызванных пожарных. Если вы будете "контролировать" эту переменную (например, рассматривать только пожары определенной величины), то исходная корреляция (между ущербом и числом пожарных) либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является ее агентом. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключенное) влияние определенных переменных.
Являются ли коэффициенты корреляции "аддитивными"? Нет, не являются. Например, усредненный коэффициент корреляции, вычисленный по нескольким выборкам, не совпадает со "средней корреляцией" во всех этих выборках. Причина в том, что коэффициент корреляции не является линейной функцией величины зависимости между переменными. Коэффициенты корреляции не могут быть просто усреднены. Если вас интересует средний коэффициент корреляции, следует преобразовать коэффициенты корреляции в такую меру зависимости, которая будет аддитивной. Например, до того, как усреднить коэффициенты корреляции, их можно возвести в квадрат, получить коэффициенты детерминации, которые уже будут аддитивными, или преобразовать корреляции в z значения Фишера, которые также аддитивны.
Как определить,
являются ли два коэффициента корреляции значимо
различными. Имеется критерий, позволяющий
оценить значимость различия двух коэффициентов
корреляциями. Результат применения критерия
зависит не только от величины разности этих
коэффициентов, но и от объема выборок и величины
самих этих коэффициентов. В соответствии с ранее
обсуждаемыми принципами, чем больше объем
выборки, тем меньший эффект мы можем значимо
обнаружить. Вообще говоря, в соответствии с общим
принципом, надежность коэффициента корреляции
увеличивается с увеличением его абсолютного
значения, относительно малые различия между
большими коэффициентами могут быть значимыми.
Например, разница .10 между двумя корреляциями
может не быть значимой, если коэффициенты равны
.15 и .25, хотя для той же выборки разность 0.10 может
оказаться значимой для коэффициентов .80 и .90.
| В начало |
t-критерий для независимых выборок
Цель, предположения. t-критерий является наиболее часто используемым методом обнаружения различия между средними двух выборок. Например, t-критерий можно использовать для сравнения средних показателей группы пациентов, принимавших определенное лекарство, с контрольной группой, где принималось безвредное лекарство. Теоретически, t-критерий может применяться, даже если размеры выборок очень небольшие (например, 10; некоторые исследователи утверждают, что можно исследовать выборки меньшего размера), и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны (см. также Элементарные понятия статистики). Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности. Равенство дисперсий в двух группах можно проверить с помощью F критерия или использовать более устойчивый критерий Левена. Если условия применимости t-критерия не выполнены, следует использовать непараметрические альтернативы t-критерия (см. Непараметрическая статистика и подгонка распределения).
p-уровень значимости t-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве средних двух выборок, когда в действительности эта гипотеза имеет место. Иными словами, он равен вероятности ошибки принять гипотезу о неравенстве средних, когда в действительности средние равны. Некоторые исследователи предлагают, в случае, когда рассматриваются отличия только в одном направлении (например, рассматривается альтернатива: среднее в первой группе больше (меньше), чем среднее во второй), использовать одностороннее t-распределение и делить р-уровень двустороннего t-критерия пополам. Другие предлагают всегда работать со стандартным двусторонним t-критерием.
См. также, t распределение Стьюдента.
Расположение
данных. Чтобы применить t-критерий для
независимых выборок, требуется, по крайней мере,
одна независимая (группирующая) переменная
(например, Пол: мужчина/женщина) и одна
зависимая переменная (например, тестовое
значение некоторого показателя, кровяное
давление, число лейкоцитов и т.д.). С помощью
специальных значений независимой переменной
(эти значения называются кодами, например, мужчина
и женщина) данные разбиваются на две группы.
Можно произвести анализ следующих данных с
помощью t-критерия, сравнивающего среднее WCC
для мужчин и женщин.
| ПОЛ | WCC | |
|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 наблюдение 4 наблюдение 5 |
мужчина мужчина мужчина женщина женщина |
111 110 109 102 104 |
| среднее WCC для
мужчин = 110 среднее WCC для женщин = 103 |
||
Графики t-критериев. Анализ данных с помощью t-критерия, сравнения средних и меры отклонения от среднего в группах можно производить с помощью диаграмм размаха (см. график ниже).
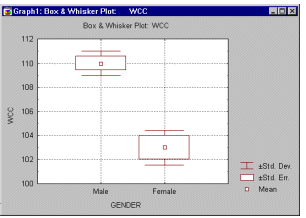
Эти графики позволяют визуально оценить степень зависимости между группирующей и зависимой переменными.
Более сложные групповые сравнения. На практике часто приходится сравнивать более двух групп данных (например, имеется лекарство 1, лекарство 2 и успокоительное лекарство) или сравнивать группы, созданные более чем одной независимой переменной (например, Пол, тип Лекарства и Доза). В таких более сложных исследованиях следует использовать Дисперсионный анализ, который можно рассматривать как обобщение t-критерия. Фактически в случае однофакторного сравнения двух групп, дисперсионный анализ дает результаты, идентичные t-критерию (t**2 [ст.св.] = F[1,ст.св.]. Однако, если план существенно более сложный, ANOVA предпочтительнее t-критерия (даже если используется последовательность t-критериев).
| В начало |
t-критерий для зависимых выборок
Внутригрупповая вариация. Как объясняется в разделе Элементарные понятия статистики, степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, "грубая разность" между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Например, если среднее WCC (число лейкоцитов - White Cell Count) равнялось 102 для мужчин и 104 для женщин, то разность внутригрупповых средних только на величину 2 будет чрезвычайно важной, когда все значения WCC мужчин лежат в интервале от 101 до 103, а все значения WCC женщин - в интервале 103 - 105. В этом случае можно довольно хорошо предсказать WCC (значение зависимой переменной) исходя из пола субъекта (независимой переменной). Однако если та же разность 2 получена из сильно разбросанных данных (например, изменяющихся в пределах от 0 до 200), то этой разностью вполне можно пренебречь. Таким образом, можно сказать, что уменьшение внутригрупповой вариации увеличивает чувствительность критерия.
Цель. t-критерий для зависимых выборок очень полезен в тех довольно часто возникающих на практике ситуациях, когда важный источник внутригрупповой вариации (или ошибки) может быть легко определен и исключен из анализа. Например, это относится к экспериментам, в которых две сравниваемые группы основываются на одной и той же совокупности наблюдений (субъектов), которые тестировались дважды (например, до и после лечения, до и после приема лекарства). В подобных экспериментах значительная часть внутригрупповой изменчивости (вариации) в обеих группах может быть объяснена индивидуальными различиями субъектов. Заметим, что на самом деле, такая ситуация не слишком отличается от той, когда сравниваемые группы совершенно независимы (см. t-критерий для независимых выборок), где индивидуальные отличия также вносят вклад в дисперсию ошибки. Однако в случае независимых выборок, вы ничего не сможете поделать с этим, т.к. не сможете определить (или "удалить") часть вариации, связанную с индивидуальными различиями субъектов. Если та же самая выборка тестируется дважды, то можно легко исключить эту часть вариации. Вместо исследования каждой группы отдельно и анализа исходных значений, можно рассматривать просто разности между двумя измерениями (например, "до приема лекарства" и "после приема лекарства") для каждого субъекта. Вычитая первые значения из вторых (для каждого субъекта) и анализируя затем только эти "чистые (парные) разности", вы исключите ту часть вариации, которая является результатом различия в исходных уровнях индивидуумов. Именно так и проводятся вычисления в t-критерии для зависимых выборок. В сравнении с t-критерием для независимых выборок, такой подход дает всегда "лучший" результат (критерий становится более чувствительным).
Предположения. Теоретические предположения t-критерия для независимых выборок относятся также к критерию для зависимых выборок. Это означает, что попарные разности должны быть нормально распределены. Если это не выполняется, то можно воспользоваться одним из альтернативных непараметрических критериев.
См. также, t распределение Стьюдента.
Расположение данных. Вы можете применять t-критерий для зависимых выборок к любой паре переменных в наборе данных. Заметим, применение этого критерия мало оправдано, если значения двух переменных несопоставимы. Например, если вы сравниваете среднее WCC в выборке пациентов до и после лечения, но используете различные методы вычисления количественного показателя или другие единицы во втором измерении, то высоко значимые значения t-критерия могут быть получены искусственно, именно за счет изменения единиц измерения. Следующий набор данных может быть проанализирован с помощью t-критерия для зависимых выборок.
| WCC до |
WCC после |
|
|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 наблюдение 4 наблюдение 5 ... |
111.9 109 143 101 80 ... |
113 110 144 102 80.9 ... |
| средняя разность между WCC "до" и "после" = 1 |
||
Средняя разность между показателями в двух
столбцах относительно мала (d=1) по сравнению с
разбросом данных (от 80 до 143, в первой выборке). Тем
не менее t-критерий для зависимых выборок
использует только парные разности,
"игнорируя" исходные численные значения и
их вариацию. Таким образом, величина этой
разности 1 будет сравниваться не с разбросом
исходных значений, а с разбросом индивидуальных
разностей, который относительно мал: 0.2 (от 0.9
в наблюдении 5 до 1.1 в наблюдении 1). В этой
ситуации разность 1 очень большая и может
привести к значимому t-значению.
Матрицы t-критериев. t-критерий для зависимых выборок может быть вычислен для списков переменных и просмотрен далее как матрица. Пропущенные данные при этом обрабатываются либо построчно, либо попарно, точно так же как при вычислении корреляционных матриц. Все те предостережения, которые относились к использованию этих методов обработки пропусков при вычислении матриц коэффициентов корреляций, остаются в силе при вычислении матриц t-критериев. Именно, возможно:
Более сложные групповые сравнения. Если имеется более двух "зависимых выборок" (например, до лечения, после лечения способом 1 и после лечения способом 2), то можно использовать дисперсионный анализ с повторными измерениями. Повторные измерения в дисперсионном анализе (ANOVA) можно рассматривать как обобщение t-критерия для зависимых выборок, позволяющие увеличить чувствительность анализа. Например, можно одновременно контролировать не только базовый уровень зависимой переменной, но и другие факторы, а также включать в план эксперимента более одной зависимой переменной (многомерный дисперсионный анализ MANOVA; более подробно см. ANOVA/MANOVA).
| В начало |
Внутригрупповые описательные статистики и корреляции (группировка)
Цель. Процедура вычисляет описательные статистики и корреляции для зависимых переменных в каждой из нескольких групп, определенных одной или большим числом группирующих (независимых) переменных.
Расположение данных. В приводимом ниже примере значения зависимой переменной WCC (число лейкоцитов - White Cell Count) разбиваются на группы кодами двух независимых переменных: Пол (значения: мужчины и женщины) и Рост (значения: высокий и низкий).
| ПОЛ | РОСТ | WCC | |
|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 наблюдение 4 наблюдение 5 ... |
мужчина мужчина мужчина женщина женщина ... |
низкий высокий высокий высокий низкий ... |
101 110 92 112 95 ... |
Результаты группировки представляются
следующим образом (предполагается, что Пол -
первая независимая переменная, а Рост -
вторая).
| Вся выборка Среднее=100 СтдОткл=13 N=120 |
|||
| Мужчины Среднее=99 СтдОткл=13 N=60 |
Женщины Среднее=101 СтдОткл=13 N=60 |
||
| Высокие/мужчины Среднее=98 СтдОткл=13 N=30 |
Низкие/мужчины Среднее=100 СтдОткл=13 N=30 |
Высокие/женщины Среднее=101 СтдОткл=13 N=30 |
Низкие/женщины Среднее=101 СтдОткл=13 N=30 |
Описательные статистики, расположенные в
середине таблицы, определяются выбранным
порядком независимых переменных. Например, в
таблице приведены средние значения для "всех
мужчин" и "всех женщин", но не показаны
средние для "всех людей высокого роста" или
для "всех людей низкого роста", которые
можно вычислить, если определить Рост как
первую группирующую переменную (а не как вторую).
Статистические тесты для группированных данных. Группировка часто используется как средство разведочного анализа данных. Обычный вопрос, который задает исследователь: являются ли группы, созданные независимыми переменными, действительно различными? Если вы интересуетесь различиями средних, то подходящим тестом является однофакторный дисперсионный анализ (ANOVA) (F критерий). Если интерес представляет различие дисперсий, то можно воспользоваться критерием однородности дисперсий.
Другие близкие методы анализа данных. Хотя в разведочном анализе данных можно строить классификацию с более чем одной независимой переменной, статистические процедуры, используемые для их анализа, предполагают, что существует только один группирующий фактор (даже если фактически результаты получаются комбинированием определенного числа группирующих переменных). Таким образом, эти статистики не обнаруживают и даже не принимают во внимание наличие возможных взаимодействий между группирующими переменными, когда в действительности такие взаимодействия могут иметь место. Например, вполне естественно допустить, что имеются различия между влиянием одной независимой переменной на зависимую переменную на разных уровнях другой независимой переменной (например, высокие люди могут иметь более низкий показатель WCC, чем низкие, однако, возможно, это относится только к мужчинам; см. "дерево" данных выше). Вы можете объяснить подобные эффекты, проверяя группировку "визуально" (в таблицах и на графиках) и используя различный порядок независимых переменных. Однако величина или значимость таких эффектов не может быть оценена здесь статистически.
Апостериорные сравнения средних. Обычно после получения статистически значимого результата в дисперсионном анализе (ANOVA) желательно знать, какие средние вызвали наблюдаемый эффект (например, какие группы особенно сильно отличаются друг от друга). Конечно, можно выполнить серию простых t-критериев, чтобы сравнить все возможные пары средних. Однако в связи с большим числом парных сравнений, такая процедура чисто случайно увеличивает шансы получения значимого результата. Представьте, вы имеете 20 выборок, по 10 случайных чисел в каждой, и вычислили для них средние. Далее возьмите наибольшее среднее и сравните с наименьшим средним. t-критерий для независимых выборок будет проверять, значимо или нет отличаются эти средние, предполагая, что имеет дело с двумя выборками. Процедуры апостериорного сравнения специально рассчитаны так, чтобы учитывать более двух выборок.
Группировка в сравнении с дискриминантным анализом.
Группировку можно рассматривать как первый шаг к другому типу анализа, который исследует различия между группами: Дискриминантный анализ. Аналогично классификации, дискриминантный анализ исследует различия между группами, построенными с помощью значений (кодов) независимой (группирующей) переменной. Однако в дискриминантном анализе, как правило, одновременно рассматривается более одной независимой переменной и определяются "типы" (классы) значений этих переменных. Именно, в дискриминантном анализе находят такие линейные комбинации зависимых переменных, которые наилучшим образом определяют принадлежность наблюдения к определенному классу, причем число классов известно заранее. В частности, с помощью дискриминантного анализа можно проанализировать различия между тремя группами людей, выбравших определенную профессию (например, юрист, физик, инженер), основываясь на их успехах в школе по определенным дисциплинам. Можно утверждать, что этот анализ "объяснит" выбор профессии успехами по определенным предметам. Таким образом, дискриминантный анализ можно рассматривать как "естественное развитие" простой группировки.
Группировка в сравнении c таблицами частот. Другой вид анализа, который не может быть непосредственно проведен с помощью группировки - это сравнения частот (n) в различных группах. Часто значения n в различных ячейках не равны между собой, потому что отнесение субъекта к определенной группе является следствием некоторых субъективных установок экспериментатора, а не результатом случайного выбора. Однако если случайный выбор имеет место, то неравенство частот n в различных группах заставляет предположить, что независимые переменные на самом деле связаны между собой. Например, кросстабуляция уровней независимых переменных Возраст и Образование наиболее вероятно не создаст группы равной величины n, потому что степень образования различна для разных возрастов. Если вы хотите провести такие сравнения, то можете изучить определенные частоты в таблицах сопряженности и испытать различные способы упорядочивания независимых переменных. Однако, для того, чтобы подвергнуть разности частот статистическому исследованию, следует воспользоваться таблицами частот и таблицами сопряженности. Для продвинутого анализа сложных многовходовых таблиц (таблиц со многими входами) используйте Логлинейный анализ или Анализ соответствий.
Графическое представление группировки. Графики часто позволяют обнаружить эффекты (как предполагаемые, так и неожиданные) быстрее, а иногда "лучше", чем численные методы. Категоризованные графики дают возможность строить графики средних, распределений, корреляций и т.д. "на пересечении" групп в соответствующих таблицах (например, категоризованные гистограммы, категоризованные вероятностные графики, категоризованные диаграммы размаха). Следующий график представляет собой категоризованную гистограмму, позволяющую быстро оценить вид данных в каждой группе (группа1-мужчины, группа2-женщины, и т.д.).
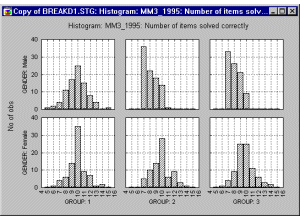
Категоризованная диаграмма размаха (на следующем графике) показывает различия в корреляциях зависимых переменных по группам.
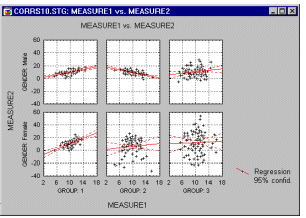
Дополнительно, если программное обеспечение обладает возможностями закрашивания, то вы можете выбрать (т.е. выделить) все точки в матричной диаграмме рассеяния, которые принадлежат к определенной группе, для того чтобы определить, как соответствующие точкам наблюдения влияют на связи между другими переменными в том же наборе данных.
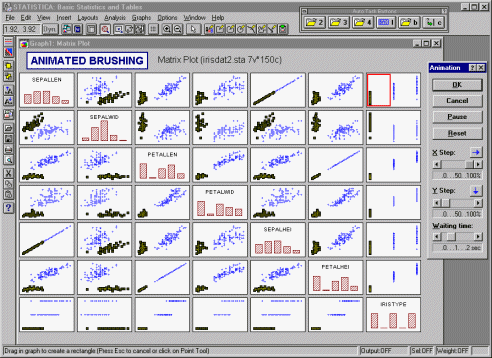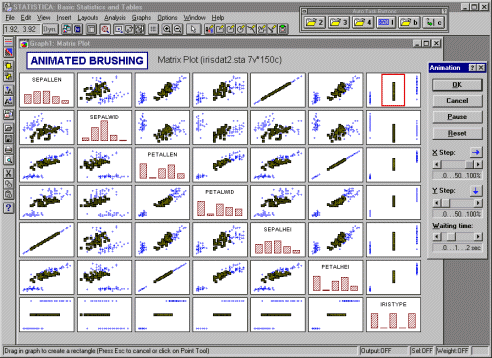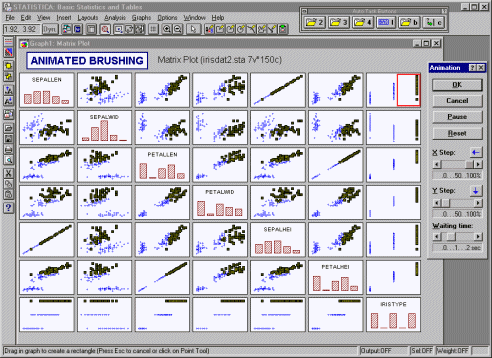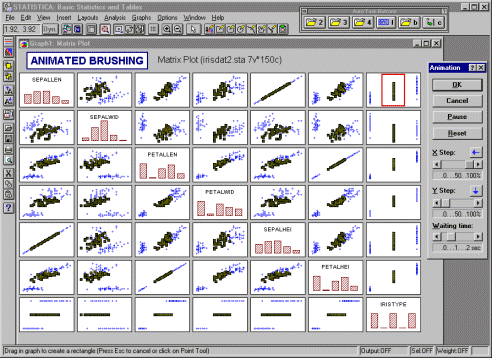
| В начало |
Таблицы частот
Цель. Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики). Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:
| STATISTICA ОСНОВНЫЕ СТАТИСТИКИ |
ФУТБОЛ: "Просмотр футбола" | |||
|---|---|---|---|---|
| Категория | Частота | Кумулят. частота |
Процент | Кумулят. процент |
| ВСЕГДА: Всегда
интересуюсь ОБЫЧНО: Обычно интересуюсь ИНОГДА: Иногда интересуюсь НИКОГДА: Никогда интересуюсь Пропущено |
39 16 26 19 0 |
39 55 81 100 100 |
39.00000 16.00000 26.00000 19.00000 0.00000 |
39.0000 55.0000 81.0000 100.0000 100.0000 |
Таблица показывает частоты, кумулятивные
(накопленные) частоты, процент, кумулятивный
процент респондентов, выразивших свой интерес к
просмотру футбольных матчей в следующей шкале: (1)
Всегда интересуюсь, (2) Обычно интересуюсь,
(3) Иногда интересуюсь или (4) Никогда не
интересуюсь.
Приложения. Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число мужчин и женщин, выразивших симпатию тому или иному политическому деятелю, число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.
| В начало |
Таблицы сопряженности и таблицы флагов и заголовков
Цель и расположение данных. Кросстабуляция - это процесс объединения двух (или нескольких) таблиц частот так, что каждая ячейка (клетка) в построенной таблице представляется единственной комбинацией значений или уровней табулированных переменных. Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Исследуя эти частоты, можно определить связи между табулированными переменными. Обычно табулируются категориальные (номинальные) переменные или переменные с относительно небольшим числом значений. Если вы хотите табулировать непрерывную переменную (например, доход), то вначале ее следует перекодировать, разбив диапазон изменения на небольшое число интервалов (например, доход: низкий, средний, высокий).
Таблицы 2x2. Простейшая форма кросстабуляции - это таблица сопряженности 2 x 2, в которой значения двух переменных "пересечены" (сопряжены) на разных уровнях и каждая переменная принимает только два значения, т.е. имеет два уровня (поэтому таблица называется "2 на 2"). К примеру, пусть проводится исследование, в котором мужчины и женщины опрашиваются о том, какой напиток они предпочитают (газированную воду марки A или газированную воду марки B); файл данных может быть таким:
| ПОЛ | ГАЗ. ВОДА | |
|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 наблюдение 4 наблюдение 5 ... |
мужчина женщина женщина женщина мужчина ... |
A B B A B ... |
Результаты кросстабуляции этих переменных
выглядят следующим образом.
| ГАЗ. ВОДА: A | ГАЗ. ВОДА: B | ||
|---|---|---|---|
| ПОЛ: мужчина | 20 (40%) | 30 (60%) | 50 (50%) |
| ПОЛ: женщина | 30 (60%) | 20 (40%) | 50 (50%) |
| 50 (50%) | 50 (50%) | 100 (100%) |
Каждая ячейка таблицы содержит единственную
комбинацию значений двух табулированных
переменных (в строке - указана переменная Пол
в столбце - переменная марка воды). Числа в каждой
ячейке, на пересечении определенной строки и
определенного столбца, показывают, сколько
наблюдений соответствует данным уровням
факторов. В целом таблица показывает, что женщины
больше мужчин предпочитают газированную воду
марки A, мужчины больше женщин предпочитают
марку B. Таким образом, пол и предпочтение
могут быть зависимыми (позже будет показано, как
эту связь измерить статистически).
Маргинальные частоты. Значения, расположенные по краям таблицы сопряженности - это обычные таблицы частот (с одним входом) для рассматриваемых переменных. Так как эти частоты располагаются на краях таблицы, то они называются маргинальными. Маргинальные значения важны, т.к. позволяют оценить распределение частот в отдельных столбцах и строках таблицы. Например, 40% и 60% мужчин и женщин (соответственно), выбравших марку A (см. первый столбец таблицы), не могли бы показать какой-либо связи между переменными Пол и Газ.вода, если бы маргинальные частоты переменной Пол были также 40% и 60%. В этом случае они просто отражали бы разную долю мужчин и женщин, участвующих в опросе. Таким образом, различие в распределении частот в строках (или столбцах) отдельных переменных и в соответствующих маргинальных частотах дают информацию о связи переменных.
Проценты по столбцам, по строкам и проценты от общего числа наблюдений. Пример в предыдущем разделе показывает, что для оценки связи между табулированными переменными, необходимо сравнить маргинальные и индивидуальные частоты в таблице. Такие сравнения легче проводить, имея дело с относительными частотами или процентами.
Графическое представление таблиц сопряженности. В целях исследования отдельные строки и столбцы таблицы удобно представлять в виде графиков. Полезно также отобразить целую таблицу на отдельном графике. Таблицы с двумя входами можно изобразить на 3-мерной гистограмме. Другой способ визуализации таблиц сопряженности - построение категоризованной гистограммы, в которой каждая переменная представлена индивидуальными гистограммами на каждом уровне другой переменной. Преимущество 3М гистограммы в том, что она позволяет представить на одном графике таблицу целиком. Достоинство категоризованного графика в том, что он дает возможность точно оценить отдельные частоты в каждой ячейке.
Таблицы флагов и заголовков. Таблицы флагов и заголовков или, кратко, таблицы заголовков позволяют отобразить несколько двувходовых таблиц в сжатом виде. Этот тип таблиц можно объяснить на примере файла интересов к спорту (см. таблицу ниже). Для краткости, в таблице изображены только строки для категорий Всегда и Обычно.
| STATISTICA ОСНОВНЫЕ СТАТИСТИКИ |
Таблица флагов и
заголовков: Проценты по строкам |
||
|---|---|---|---|
| Фактор | ФУТБОЛ ВСЕГДА |
ФУТБОЛ ОБЫЧНО |
Всего по строке |
| БЕЙСБОЛ: ВСЕГДА БЕЙСБОЛ: ОБЫЧНО |
92.31 61.54 |
7.69 38.46 |
66.67 33.33 |
| БЕЙСБОЛ: Всего | 82.05 | 17.95 | 100.00 |
| ТЕННИС: ВСЕГДА ТЕННИС: ОБЫЧНО |
87.50 87.50 |
12.50 12.50 |
66.67 33.33 |
| ТЕННИС: Всего | 87.50 | 12.50 | 100.00 |
| БОКС: ВСЕГДА БОКС: ОБЫЧНО |
77.78 100.00 |
22.22 0.00 |
52.94 47.06 |
| БОКС : Всего | 88.24 | 11.76 | 100.00 |
Интерпретация таблиц заголовков. В приведенной выше таблице результатов представлены три двувходовые таблицы, в которых интерес к Футболу сопряжен с интересом к Бейсболу, Теннису и Боксу. Таблица содержит информацию о процентах по столбцам, поэтому суммы по строкам равны 100%. Например, число в левом верхнем углу таблицы результатов (92.31) показывает, что 92.31 процентов всех респондентов ответили, что им всегда интересно смотреть футбол и всегда интересно смотреть баскетбол. Если вы посмотрите следующую часть таблицы, то увидите, что процент тех, кому всегда интересно смотреть футбол и всегда интересно смотреть теннис, равен 87.50; для бокса этот процент составляет 77.78. Проценты в столбце (Всего по строке), показанные после каждого набора переменных, всегда связаны с общим числом наблюдений.
Многовходовые таблицы с категориальными переменными. Когда кросстабулируются только две переменные, результирующая таблица называется двувходовой. Конечно, общую идею кросстабулирования можно обобщить на большее число переменных. В примере с "газированной водой" (см. выше) добавим третью категориальную переменную с информацией о городе, в котором проводилось исследование (Москва или Петербург).
| ПОЛ | ГАЗ. ВОДА | ГОРОД | |
|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 наблюдение 4 наблюдение 5 ... |
мужчина женщина женщина женщина мужчина ... |
A B B A B ... |
МОСКВА ПЕТЕРБУРГ МОСКВА МОСКВА ПЕТЕРБУРГ ... |
Кросстабуляция этих 3-х переменных представлена
в следующей таблице:
| ГОРОД: ПЕТЕРБУРГ | ГОРОД: МОСКВА | |||||
|---|---|---|---|---|---|---|
| ГАЗ. ВОДА: A | ГАЗ. ВОДА: B | ГАЗ. ВОДА: A | ГАЗ. ВОДА: B | |||
| Пол:мужчина | 20 | 30 | 50 | 5 | 45 | 50 |
| Пол:женщина | 30 | 20 | 50 | 45 | 5 | 50 |
| 50 | 50 | 100 | 50 | 50 | 100 | |
Теоретически любое число переменных может быть
кросстабулировано в одной многовходовой
таблице. Однако на практике возникают сложности
с проверкой и "пониманием" таких таблиц,
даже если они содержат более четырех переменных.
Рекомендуется анализировать зависимости между
факторами в таких таблицах с помощью более
продвинутых методов, таких как Логлинейный анализ или Анализ соответствий.
Графическое представление многовходовых таблиц. Вы можете построить "дважды категоризованные" гистограммы, 3М гистограммы
или линейные графики, позволяющие свести частоты для более чем 3-х факторов в один график.
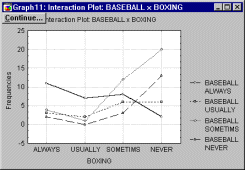
Наборы (каскады) графиков используются для интерпретации сложных многовходовых таблиц (как показано на следующем графике).
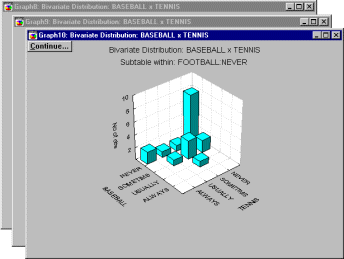
Статистики таблиц сопряженности
Обзор. Таблицы сопряженности позволяют измерить связи между кросстабулированными переменными. Следующая таблица отчетливо показывает сильную связь между двумя переменными: переменная Возраст (Взрослый или Ребенок) и переменная - предпочитаемое Печенье (сорт A или сорт B).
| ПЕЧЕНЬЕ: A | ПЕЧЕНЬЕ: B | ||
|---|---|---|---|
| ВОЗРАСТ: ВЗРОСЛЫЙ | 50 | 0 | 50 |
| ВОЗРАСТ: РЕБЕНОК | 0 | 50 | 50 |
| 50 | 50 | 100 |
Из таблицы видно, что все взрослые выбирают
печенье A, а все дети печенье B. В данном
случае, нет оснований сомневаться в надежности
этого факта. Взглянув на таблицу, мало кто
усомнится, что между предпочтениями детей и
взрослых имеется отчетливое различие. Однако
наблюдаемые на практике связи значительно
слабее, и поэтому возникает вопрос: как измерить
связи между табулированными переменными и
оценить их надежность (статистическую
значимость). Далее обсуждаются самые общие меры
связи между двумя категоризованными
переменными. Методы, используемые для анализа
связей между более чем двумя переменными в
таблицах высокого порядка, обсуждаются в
разделах Логлинейный
анализ и Анализ
соответствий.
Критерий хи-квадрат Пирсона. Хи-квадрат Пирсона - это наиболее простой критерий проверки значимости связи между двумя категоризованными переменными. Критерий Пирсона основывается на том, что в двувходовой таблице ожидаемые частоты при гипотезе "между переменными нет зависимости" можно вычислить непосредственно. Представьте, что 20 мужчин и 20 женщин опрошены относительно выбора газированной воды (марка A или марка B). Если между предпочтением и полом нет связи, то естественно ожидать равного выбора марки A и марки B для каждого пола.
Значение статистики хи-квадрат и ее уровень значимости зависит от общего числа наблюдений и количества ячеек в таблице. В соответствии с принципами, обсуждаемыми в разделе Элементарные понятия статистики, относительно малые отклонения наблюдаемых частот от ожидаемых будет доказывать значимость, если число наблюдений велико.
Имеется только одно существенное ограничение использования критерия хи-квадрат (кроме очевидного предположения о случайном выборе наблюдений), которое состоит в том, что ожидаемые частоты не должны быть очень малы. Это связано с тем, что критерий хи-квадрат по своей природе проверяет вероятности в каждой ячейке; и если ожидаемые частоты в ячейках, становятся, маленькими, например, меньше 5, то эти вероятности нельзя оценить с достаточной точностью с помощью имеющихся частот. Дальнейшие обсуждения см. в работах Everitt (1977), Hays (1988) или Kendall and Stuart (1979).
Критерий хи-квадрат (метод максимального правдоподобия). Максимум правдоподобия хи-квадрат предназначен для проверки той же самой гипотезы относительно связей в таблицах сопряженности, что и критерий хи-квадрат Пирсона. Однако его вычисление основано на методе максимального правдоподобия. На практике статистика МП хи-квадрат очень близка по величине к обычной статистике Пирсона хи-квадрат. Подробнее об этой статистике можно прочитать в работах Bishop, Fienberg, and Holland (1975) или Fienberg (1977). В разделе Логлинейный анализ эта статистика обсуждается подробнее.
Поправка Йетса. Аппроксимация статистики хи-квадрат для таблиц 2x2 с малыми числом наблюдений в ячейках может быть улучшена уменьшением абсолютного значения разностей между ожидаемыми и наблюдаемыми частотами на величину 0.5 перед возведением в квадрат (так называемая поправка Йетса). Поправка Йетса, делающая оценку более умеренной, обычно применяется в тех случаях, когда таблицы содержат только малые частоты, например, когда некоторые ожидаемые частоты становятся меньше 10 (дальнейшее обсуждение см. в Conover, 1974; Everitt, 1977; Hays, 1988; Kendall and Stuart, 1979 и Mantel, 1974).
Точный критерий Фишера. Этот критерий применим только для таблиц 2x2. Критерий основан на следующем рассуждении. Даны маргинальные частоты в таблице, предположим, что обе табулированные переменные независимы. Зададимся вопросом: какова вероятность получения наблюдаемых в таблице частот, исходя из заданных маргинальных? Оказывается, эта вероятность вычисляется точно подсчетом всех таблиц, которые можно построить, исходя из маргинальных. Таким образом, критерий Фишера вычисляет точную вероятность появления наблюдаемых частот при нулевой гипотезе (отсутствие связи между табулированными переменными). В таблице результатов приводятся как односторонние, так и двусторонние уровни.
Хи-квадрат Макнемара. Этот критерий применяется, когда частоты в таблице 2x2 представляют зависимые выборки. Например, наблюдения одних и тех же индивидуумов до и после эксперимента. В частности, вы можете подсчитывать число студентов, имеющих минимальные успехи по математике в начале и в конце семестра или предпочтение одних и тех же респондентов до и после рекламы. Вычисляются два значения хи-квадрат: A/D и B/C. A/D хи-квадрат проверяет гипотезу о том, что частоты в ячейках A и D (верхняя левая, нижняя правая) одинаковы. B/C хи-квадрат проверяет гипотезу о равенстве частот в ячейках B и C (верхняя правая, нижняя левая).
Коэффициент Фи. Фи-квадрат представляет собой меру связи между двумя переменными в таблице 2x2. Его значения изменяются от 0 (нет зависимости между переменными; хи-квадрат = 0.0) до 1 (абсолютная зависимость между двумя факторами в таблице). Подробности см. в Castellan and Siegel (1988, стр. 232).
Тетрахорическая корреляция. Эта статистика вычисляется (и применяется) только для таблиц сопряженности 2x2. Если таблица 2x2 может рассматриваться как результат (искусственного) разбиения значений двух непрерывных переменных на два класса, то коэффициент тетрахорической корреляции позволяет оценить зависимость между двумя этими переменными.
Коэффициент сопряженности. Коэффициент сопряженности представляет собой основанную на статистике хи-квадрат меру связи признаков в таблице сопряженности (предложенную Пирсоном). Преимущество этого коэффициента перед обычной статистикой хи-квадрат в том, что он легче интерпретируется, т.к. диапазон его изменения находится в интервале от 0 до 1 (где 0 соответствует случаю независимости признаков в таблице, а увеличение коэффициента показывает увеличение степени связи). Недостаток коэффициента сопряженности в том, что его максимальное значение "зависит" от размера таблицы. Этот коэффициент может достигать значения 1 только, если число классов не ограничено (см. Siegel, 1956, стр. 201).
Интерпретация мер связи. Существенный недостаток мер связи (рассмотренных выше) связан с трудностью их интерпретации в обычных терминах вероятности или "доли объясненной вариации", как в случае коэффициента корреляции r Пирсона (см. Корреляции). Поэтому не существует одной общепринятой меры или коэффициента связи.
Статистики, основанные на рангах. Во многих задачах, возникающих на практике, мы имеем измерения лишь в порядковой шкале (см. Элементарные понятия статистики). Особенно это относится к измерениям в области психологии, социологии и других дисциплинах, связанных с изучением человека. Предположим, вы опросили некоторое множество респондентов с целью выяснения их отношение к некоторым видам спорта. Вы представляете измерения в шкале со следующими позициями: (1) всегда, (2) обычно, (3) иногда и (4) никогда. Очевидно, что ответ иногда интересуюсь показывает меньший интерес респондента, чем ответ обычно интересуюсь и т.д. Таким образом, можно упорядочить (ранжировать) степень интереса респондентов. Это типичный пример порядковой шкалы. Для переменных, измеренных в порядковой шкале, имеются свои типы корреляции, позволяющие оценить зависимости.
R Спирмена. Статистику R Спирмена можно интерпретировать так же, как и корреляцию Пирсона (r Пирсона) в терминах объясненной доли дисперсии (имея, однако, в виду, что статистика Спирмена вычислена по рангам). Предполагается, что переменные измерены как минимум в порядковой шкале. Всестороннее обсуждение ранговой корреляции Спирмена, ее мощности и эффективности можно найти, например, в книгах Gibbons (1985), Hays (1981), McNemar (1969), Siegel (1956), Siegel and Castellan (1988), Kendall (1948), Olds (1949) и Hotelling and Pabst (1936).
Тау Кендалла. Статистика тау Кендалла эквивалентна R Спирмена при выполнении некоторых основных предположений. Также эквивалентны их мощности. Однако обычно значения R Спирмена и тау Кендалла различны, потому что они отличаются как своей внутренней логикой, так и способом вычисления. В работе Siegel and Castellan (1988) авторы выразили соотношение между этими двумя статистиками следующим неравенством:
-1 < = 3 * Тау Кендалла - 2 * R Спирмена < = 1
Более важно то, что статистики Кендалла тау и Спирмена R имеют различную интерпретацию: в то время как статистика R Спирмена может рассматриваться как прямой аналог статистики r Пирсона, вычисленный по рангам, статистика Кендалла тау скорее основана на вероятности. Более точно, проверяется, что имеется различие между вероятностью того, что наблюдаемые данные расположены в том же самом порядке для двух величин и вероятностью того, что они расположены в другом порядке. Kendall (1948, 1975), Everitt (1977), и Siegel and Castellan (1988) очень подробно обсуждают тау Кендалла. Обычно вычисляется два варианта статистики тау Кендалла: taub и tauc. Эти меры различаются только способом обработки совпадающих рангов. В большинстве случаев их значения довольно похожи. Если возникают различия, то, по-видимому, самый безопасный способ - рассматривать наименьшее из двух значений.
Коэффициент d Соммера: d(X|Y), d(Y|X). Статистика d Соммера представляет собой несимметричную меру связи между двумя переменными. Эта статистика близка к taub (см. Siegel and Castellan, 1988, стр. 303-310).
Гамма-статистика. Если в данных имеется много совпадающих значений, статистика гамма предпочтительнее R Спирмена или тау Кендалла. С точки зрения основных предположений, статистика гамма эквивалентна статистике R Спирмена или тау Кендалла. Ее интерпретация и вычисления более похожи на статистику тау Кендалла, чем на статистику R Спирмена. Говоря кратко, гамма представляет собой также вероятность; точнее, разность между вероятностью того, что ранговый порядок двух переменных совпадает, минус вероятность того, что он не совпадает, деленную на единицу минус вероятность совпадений. Таким образом, статистика гамма в основном эквивалентна тау Кендалла, за исключением того, что совпадения явно учитываются в нормировке. Подробное обсуждение статистики гамма можно найти у Goodman and Kruskal (1954, 1959, 1963, 1972), Siegel (1956) и Siegel and Castellan (1988).
Коэффициенты неопределенности. Эти коэффициенты измеряют информационную связь между факторами (строками и столбцами таблицы). Понятие информационной зависимости берет начало в теоретико-информационном подходе к анализу таблиц частот, можно обратиться к соответствующим руководствам для разъяснения этого вопроса (см. Kullback, 1959; Ku and Kullback, 1968; Ku, Varner, and Kullback, 1971; см. также Bishop, Fienberg, and Holland, 1975, стр. 344-348). Статистика S(Y,X) является симметричной и измеряет количество информации в переменной Y относительно переменной X или в переменной X относительно переменной Y. Статистики S(X|Y) и S(Y|X) выражают направленную зависимость.
Многомерные отклики и дихотомии. Переменные типа многомерных откликов и многомерных дихотомий возникают в ситуациях, когда исследователя интересуют не только "простые" частоты событий, но также некоторые (часто неструктурированные) качественные свойства этих событий. Природу многомерных переменных (факторов) лучше всего понять на примерах.
Многомерные отклики. Представьте, что в процессе большого маркетингового исследования, вы попросили покупателей назвать 3 лучших, с их точки зрения, безалкогольных напитка. Обычный вопрос может выглядеть следующим образом:
Напишите ниже три ваших любимых безалкогольных напитка:
1:__________ 2:__________ 3:__________
Анкета содержит от 0 до 3 ответов. Очевидно, список напитков может быть очень большим. Ваша цель - свести результаты в таблицу, в которой, например, будет подсчитан процент респондентов, предпочитающих определенный напиток.
Следующий шаг после получения анкет - занесение ответов в файл данных. Предположим, в ответах упоминалось 50 различных напитков. Вы могли бы, конечно, создать 50 переменных - одну для каждого напитка, рассмотреть респондентов как наблюдения (строки таблицы), ввести код 1 для респондента и переменной, если он предпочитают данный напиток (0, если нет); например:
| КОКА-КОЛА | ПЕПСИ | СПРАЙТ | . . . . | |
|---|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 ... |
0 1 0 ... |
1 1 0 ... |
0 0 1 ... |
Такой метод кодирования откликов, т.е.
приписывания им конкретных значений, очевидно,
"расточителен". Заметим, что каждый
респондент дает максимум 3 ответа; однако для
кодирования используется 50 переменных. (Если вы
интересуетесь только тремя напитками, то такой
метод кодирования будет успешным. Чтобы
табулировать предпочтения в выборе напитка,
следует рассмотреть 3 переменные, как одну многомерную
дихотомию; см. ниже.)
Кодирование многомерных откликов. Более разумным является следующий подход. Введите 3 переменные и определите схему кодирования для 50 напитков. Затем введите соответствующие коды (альфа метки) для значений переменных и получите таблицу следующего вида.
| Ответ 1 | Ответ 2 | Ответ 3 | |
|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 . . . |
КОКА-КОЛА СПРАЙТ ПЕРЬЕ . . . |
ПЕПСИ ФАНТА 7 АП . . . |
ДЖОЛТ ДОКТОР ПЕППЕР ОРАНЖ . . . |
Теперь, чтобы получить число респондентов,
предпочитающих определенный напиток,
рассмотрите переменные Ответ 1 - Ответ 3 как переменную
с многомерным откликом. Таблица значений такой
переменной имеет вид:
| N=500 Категория |
Частота | Процент ответов |
Процент наблюдений |
|---|---|---|---|
| КОЛА: Кока Кола ПЕПСИ: Пепси Кола СПРАЙТ: Спрайт ПЕППЕР: Доктор Пеппер . . . : . . . . |
44 43 81 74 .. |
5.23 5.11 9.62 8.79 ... |
8.80 8.60 16.20 14.80 ... |
| 842 | 100.00 | 168.40 |
Интерпретация таблиц частот с многомерными откликами. Итак, общее число респондентов в опросе n=500. Заметьте, что числа в первой колонке таблицы не составляют в сумме 500, как можно было бы ожидать, а равны 842. Вы поймете, почему это так, если вспомните, что каждый респондент может дать несколько ответов. Возвращаясь к примеру, видим, что первое наблюдение (Кола, Пепси, Джолт) "дает" три вклада в таблицу частот: в категорию Кола, в категорию Пепси и в категорию Джолт. Второй и третий столбцы таблицы содержат проценты относительного числа ответов (второй столбец) и наблюдений (третий столбец). Таким образом, число 8.80 в первой строке и в последнем столбце таблицы означает, что 8.8% всех респондентов выбрали Кола первым, вторым или третьим пунктом ответа.
Многомерные дихотомии. Предположим, вас интересуют только Кола, Пепси и Спрайт. Как отмечалось, одним из способов кодирования является следующий:
| КОЛА | ПЕПСИ | СПРАЙТ | . . . . | |
|---|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 . . . |
1 . . . |
1 1 . . . |
1 . . . |
Здесь каждая переменная используется для одного
напитка. Код 1 будет введен в таблицу для
переменной каждый раз, когда соответствующий
респондент указал ее в своем ответе. Заметим, что
каждая переменная является дихотомией, т.к.
принимает только два значения: "1" и "не
1" (можно ввести 1 и 0, но так обычно не
делается, можно просто рассматривать 0 как
пустую ячейку или пропуск). Когда табулируются
такие значения, вы получите итоговую таблицу,
очень похожую на ту, что была показана раньше для
переменных с многомерными откликами; из нее вы
можете вычислить число и процент респондентов (и
ответов) для каждого напитка. Таким образом, вы
компактно представили три переменные - Кола, Пепси,
Спрайт одной переменной (Безалкогольные
напитки) - многомерной дихотомией.
Кросстабуляция многомерных откликов и дихотомий. Все эти типы переменных можно использовать в таблицах сопряженности. Например, вы можете объединить многомерную дихотомию Безалкогольные напитки (закодированную, как описано выше) с многомерным откликом Любимая еда (со многими категориями, например, Гамбургеры, Пицца и т.д.), а также с простой группирующей переменной Пол. Как и в таблице частот для обычных переменных, в таблице частот для многомерных переменных, можно вычислить проценты и маргинальные суммы или по общему числу респондентов или по общему числу ответов (откликов). Например, рассмотрим следующего гипотетического респондента:
| Пол | Кола | Пепси | Спрайт | Еда1 | Еда2 |
|---|---|---|---|---|---|
| женщина | 1 | 1 | РЫБА | ПИЦЦА |
Эта женщина назвала Кола и Пепси своими
любимыми напитками, а Рыбу и Пиццу -
любимыми блюдами. В полной таблице сопряженности
этот респондент будет представлен следующими
наборами:
| Еда | . . . | Всего ответов |
||||
|---|---|---|---|---|---|---|
| Пол | Напиток | ГАМБУРГЕР | РЫБА | ПИЦЦА | . . . | |
| женщина мужчина |
КОЛА ПЕПСИ СПРАЙТ КОЛА ПЕПСИ СПРАЙТ |
|
X X |
X X |
|
2 2 |
Данный респондент учитывается в таблице 4 раза.
Дополнительно, он будет считаться дважды в
столбце Женщина - КОЛА маргинальных частот,
если этот столбец выводится для представления
общего числа откликов. Если пользователь
запрашивает маргинальные суммы, вычисленные как
общее число респондентов, тогда этот респондент
будет учитываться только один раз.
Парная кросстабуляция переменных с многомерными откликами. Особенность процедуры табулирования многомерных переменных состоит в их попарном рассмотрении. Лучше всего показать это на простом примере. Предположим, проводится обследование нынешних и бывших домовладений респондента. Вы попросили респондента описать три последних дома, которыми он владел (включая тот, которым он владеет в данный момент). Естественно, для некоторых из респондентов нынешний дом является самым первым (до этого они не приобретали дома в частную собственность). Другие владели домами раньше. Для каждого дома респондента просят написать количество квартир и число жильцов - членов семьи. Ниже показано, как ответ одного респондента (скажем, наблюдение 112) может быть введен в файл данных:
| Наблюдение | Число комнат | 1 | 2 | 3 | Число жильцов | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|---|
| 112 | 3 | 3 | 4 | 2 | 3 | 5 |
Респондент имел три дома: первый из 3-х комнат,
второй также из 3-х комнат, третий из 4-х комнат.
Количество членов семьи также росло: в первом
доме жило 2 человека, во втором - 3, в третьем - 5.
Пусть вы хотите кросстабулировать число комнат с числом жильцов для всех респондентов (например, чтобы понять, как количество комнат связано с числом жильцов). Один из способов - создать 3 различные таблицы с двумя входами; одну таблицу для одного дома. Вы можете также рассмотреть два фактора в этом исследовании (Число комнат, Число жильцов) как переменные со многими откликами. Однако, очевидно, нет никакого смысла в приведенном примере с респондентом 112 учитывать значения 3 и 5 в ячейке Комнаты - Жильцы в таблице сопряженности (которые вы могли бы учитывать, если бы рассматривали два эти фактора как одинарные переменные с многомерными откликами). Другими словами, вы хотите игнорировать комбинацию жильцов в третьем доме с числом комнат в первом. Скорее всего, вам нужно рассматривать переменные попарно; вы хотели бы рассмотреть число комнат в первом доме вместе с числом жильцов в первом доме, число комнат во втором доме вместе с числом жильцов в нем и т.д. Так именно и происходит, когда программа выполняет парную кросстабуляцию многомерных переменных.
Заключительный комментарий. Иногда при создании сложных таблиц сопряженности с переменными - многомерными откликами и дихотомиями, возникает следующий вопрос (в ваших исследованиях): "какую дорогу выбрать" или как точно будут учитываться наблюдения в файле данных. Лучший способ проверить, как строится соответствующая таблица - рассмотреть простой пример, и по нему ясно увидеть, каким образом учитывается каждое наблюдение (какой оно вносит вклад). В примерах к разделу Кросстабуляции используется именно такой метод, для того чтобы показать, как вычисляются данные для таблиц с переменными - многомерными откликами и многомерными дихотомиями.
| В начало |
![]()
(c) Copyright StatSoft, Inc., 1984-1998
STATISTICA является торговой маркой StatSoft, Inc.