Планирование эксперимента
Обзор
Эксперименты в науке и промышленности
Экспериментальные методы широко используются как в науке, так и в промышленности, однако нередко с весьма различными целями. Обычно основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную (подробнее о понятии статистической значимости см. в главе Элементарные понятия статистики, т. I).
В условиях промышленного эксперимента основная цель обычно заключается в извлечении максимального количества объективной информации о влиянии изучаемых факторов на производственный процесс с помощью наименьшего числа дорогостоящих наблюдений. Если в научных приложениях методы дисперсионного анализа используются для выяснения реальной природы взаимодействий, проявляющейся во взаимодействии факторов высших порядков, то в промышленности учет эффектов взаимодействия факторов часто считается излишним в ходе выявления существенно влияющих факторов.
Различия в методике
Указанное отличие приводит к существенному различию методов, применяемых в науке и промышленности. Если просмотреть классические учебники по дисперсионному анализу, например, монографии Винера (1962) или Кеппеля (1982), то обнаружится, что в них, в основном, обсуждаются планы с количеством факторов не более пяти (планы же с более чем шестью факторами обычно оказываются бесполезными: подробнее см. в разделе Вводный обзор главы Дисперсионный анализ). Основное внимание в данных рассуждениях сосредоточено на выборе общезначимых и устойчивых критериев значимости. Однако если обратиться к стандартным учебникам по экспериментам в промышленности (например, Бокс, Хантер и Хантер (1978); Бокс и Дрейпер (1987); Мейсон, Ганс и Гесс (1989); Тагучи (1987)), то окажется, что в них обсуждаются, в основном, многофакторные планы (например, с 16-ю или 32-мя факторами), в которых нельзя оценить эффекты взаимодействия, и основное внимание сосредоточивается на том получении несмещенных оценок главных эффектов (или, реже, взаимодействий второго порядка) с использованием наименьшего числа наблюдений.
Это сравнение можно продолжить, но после того как вы получите более подробную информацию о планировании промышленных экспериментов, различия станут еще более очевидны. Отметим, что глава Дисперсионный анализ содержит подробное обсуждение типичных вопросов, касающихся планирования эксперимента в научных исследованиях, а модуль Дисперсионный анализ системы STATISTICA представляет исчерпывающую реализацию общей линейной модели в дисперсионном и ковариационном анализе (как одномерном, так и многомерном). Разумеется, существует немало промышленных приложений, в которых с успехом используются обычные планы дисперсионного анализа, зарекомендовавшие себя в научных исследованиях. Для того, чтобы составить более общее впечатление о совокупности методов, объединенных понятием Планирование эксперимента, будет полезно обратиться к разделу Вводный обзор главы Дисперсионный анализ.
Обзор
В следующих параграфах обсуждаются общие идеи и принципы, на которых основано планирование промышленных экспериментов, а также описываются используемые типы планов. Эти параграфы близки по своему характеру к вводным. Предполагается, что вы уже знакомы с основными идеями дисперсионного анализа и способами интерпретации главных эффектов и взаимодействий. Мы рекомендуем перечитать раздел Вводный обзор главы Дисперсионный анализ перед тем, как продолжить чтение.
Общие идеи
Обычно любая машина или станок, используемый на производстве, позволяет операторам изменять различные настройки, влияя на качество производимого продукта. Эксперименты позволяют инженеру, ответственному за производство, улучшать настройки машины, а также выяснить какие факторы вносят наиболее важный вклад в качество продукции. Использование этой информации позволяет улучшить настройки системы, достигнув оптимального качества. Чтобы проиллюстрировать эти рассуждения ниже приводится несколько примеров.
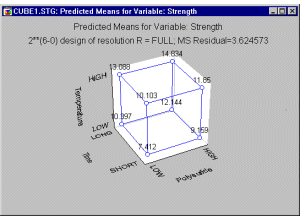
Пример 1: Производство красителей для ткани. В книге Бокса и Дрейпера (Бокс и Дрейпер (1987), стр. 115) рассказывается об эксперименте по производству некоторого красителя для ткани. В этом случае качество производимой продукции описывается насыщенностью, яркостью и стойкостью окрашеной ткани. Кроме того, необходимо уточнить, что надо изменять для получения красок различной насыщенности, яркости для удовлетворения потребительского спроса. Другими словами, в этом эксперименте нужно выявить факторы, наиболее заметно влияющие на яркость, насыщенность и стойкость производимой краски. В примере Бокса и Дрейпера рассматривается 6 различных факторов, влияние которых оценивается с помощью плана 2**(6-0) (объяснение обозначения 2**(k-p) см. ниже). Результаты эксперимента показывают, что имеется три наиболее важных фактора: Полисульфидный индекс, Время и Температура (см. Бокс и Дрейпер (1987), стр. 116). Можно представить ожидаемое воздействие на интересующую нас переменную (в данном случае светостойкость окраски) в виде так называемой кубической диаграммы. Эта диаграмма показывает ожидаемую (предсказываемую) среднюю стойкость на верхних и нижних уровнях каждого из трех факторов.

Кроме того, для каждой комбинации факторов было проведено два измерения, таким образом, план 3**(3-0) был полностью повторен или, как говорят, реплицирован.
Пример 3: Максимизация выхода химической реакции. Выход продукта многих химических реакций зависит от времени и температуры. К сожалению, эти функции не линейны и не монотонны. Другими словами, нельзя сказать: “чем больше продолжительность реакции, тем больше выход” и “чем выше температура, тем больше выход”.
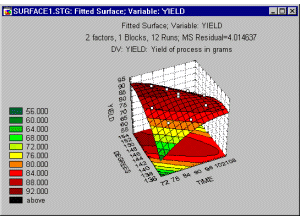
Формально цель эксперимента заключается в том, чтобы найти оптимальное положение на поверхности выхода, образованной двумя переменными: временем и температурой.
Пример 4: Проверка эффективности четырех топливных присадок. Планы на латинских квадратах обычно используются, когда интересующие нас факторы измеряются более чем на двух уровнях, а характер задачи подсказывает возможность разбиения плана на блоки. Например, представьте, что изучается 4 топливные присадки для снижения содержания в выхлопах окиси азота (смотрите монографию Бокса, Хантера и Хантера, 1978, стр. 263). Вы имеете в своем распоряжении 4 водителя и 4 автомобиля. Вам не интересен эффект влияния работы водителей или типа автомобиля на снижение концентрации окиси азота, однако, вам не хотелось бы, что бы полученные результаты относились к некоторому конкретному водителю или автомобилю (из смещения по этим факторам). Планы на латинских квадратах позволяют оценить главные эффекты всех факторов несмещенным образом. В данном примере размещение уровней воздействия в виде латинского квадрата гарантирует, что различия между водителями и автомобилями не повлияют на оценку эффекта различных топливных присадок. Пример 5: Улучшение поверхностной однородности при производстве кремниевых кристаллов. Производство надежных микропроцессоров требует высоко отлаженного производственного процесса. Отметим, что в данном примере одинаково, если не более важно, контролировать как изменчивость некоторых производственных характеристик, так и их средние значения. Например, средняя толщина поверхностного слоя поликремниевой подложки производственный процесс может быть отрегулирован превосходно, однако, если изменчивость этого параметра велика (представьте, что срез под микроскопом будет похож на ломанную линию с острыми углами), то микрочипы будут недостаточно надежными. Фадке (1989) описал, как различные характеристики производственного процесса (давление, температура кипящего слоя, давление обдувающего поток азота и т.д.) влияют на изменчивость толщины поверхностного слоя кремния на подложке. Не существует теоретической модели, которые позволяла бы инженеру предсказать, как эти факторы влияют на однородность поверхности кристаллов. Следовательно, для оптимизации производственного процесса нужно систематизировано проводить эксперименты на различных уровнях факторов. В этом случае чрезвычайно полезны так называемые Робастные планы Тагучи.Пример 6: Планы для смесей. В работе Корнелла (1990, стр. 9) приводится пример типичной задачи анализа смесей. Было проведено исследование для определения оптимального состава рыбного паштета как результата смешения различных пород рыб, идущих на его приготовление (в том числе кефаль, окунь и горбыль). В отличие от обычных экспериментов, в смеси общая сумма долей должна быть постоянна, например, равна 100%. Результаты таких экспериментов обычно представляются графически в виде тернарных графиков.

Основное ограничение - три компоненты в сумме равняются константе - выражается в треугольной форме графика.
Пример 6.1: Планы для смесей с ограничениями. В частности, в планах по изучению смесей на относительные доли компонентов можно наложить дополнительные ограничения (помимо условия постоянства их суммы). Например, предположим, что вы хотите разработать наилучший по вкусу фруктовый пунш, состоящий из смеси пяти фруктовых соков. Поскольку предполагается, что изготовленная смесь должна быть именно фруктовым пуншем, чистые смеси, состоящие только из одного фруктового сока не рассматриваются. Дополнительные ограничения на область допустимых смесей могут возникнуть из-за высокой стоимости одного из соков или по некоторым другим соображениям, поскольку некоторый конкретный сок не может иметь в смеси долю более чем, скажем, 30% (иначе фруктовый пунш был бы слишком дорог, длительность его хранения была бы невелика, пунш не мог бы производиться в больших количествах и так далее). Подобные поверхности с ограничениями представляют многочисленные трудности для практиков. Однако все они могут быть легко преодолены с помощью модуля Планирование эксперимента.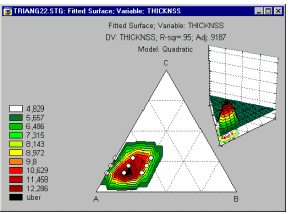
В общем случае, при заданных ограничениях ищется план эксперимента, который позволяет извлечь максимальное количество информации об интересующей нас функции отклика (например, о вкусе фруктового пунша) на выбранной многомерной поверхности.
Вычислительные проблемы
К основным видам задач, решаемых в модуле Планирование эксперимента, относятся:
Для решения задач первого вида имеется несколько подходов, реализованных в соответствующих планах экспериментов, основную идею которых можно выразить следующим образом. В общем случае, цель экспериментатора состоит в получении наиболее несмещенной (или наименее смещенной) оценки эффекта фактора вне зависимости от установок других факторов. Более точно, вы пытаетесь построить планы, в которых главные эффекты не смешаны друг с другом, а может быть даже и с взаимодействиями факторов.
Компоненты дисперсии, синтез деноминатора
Некоторые модули в STATISTICA позволяют проводить анализ планов со случайными эффектами (смотрите Методы дисперсионного анализа). Модуль Компоненты дисперсии и смешанная модель ANOVA/ANCOVA содержит различные опции для оценок компонент дисперсии для случайных эффектов, а также для проведения приближенных F - тестов, основанных на обобщенном члене ошибки. Смотрите также Методы дисперсионного анализа для знакомства с различными опциями ANOVA/ANCOVA, доступных в STATISTICA.
Выводы
Экспериментальные методы находят все большее применение в промышленности для оптимизации производственных процессов. Целью этих методов является поиск оптимальных уровней факторов, определяющих течение процесса производства. В рассмотренных примерах мы познакомили вас с основными типами планов, обычно используемыми в промышленности: планами 2**(k-p) (двухуровневыми многофакторными планами), отсеивающими планами для большего числа факторов, планами 3**(k-p) (трехуровневыми многофакторными планами), смешанными 2-х и 3-х уровневыми планами, центральными композиционными планами (или планами поверхности отклика), планами на латинских квадратах, робастными планами Тагучи, планами для смесей, а также специальными процедурами для проведения экспериментов на поверхностях с ограничениями. Интересно, что многие из этих методов прошли путь от заводских цехов до кабинетов менеджеров и аналитиков, зарекомендовав себя в задачах планирование прибыли в бизнесе, управления финансовыми потоками в банковском деле и многих других (см., например, работу Йокиама и Тагучи (1975)).Все эти методы подробно обсуждаются в следующих разделах:
Во многих случаях достаточно рассмотреть всего два уровня факторов, влияющих на производственный процесс. Например, температура проведения химического процесса может быть установлена немного ниже или немного выше заданного уровня, количество растворителя при производстве красителя можно немного увеличить или уменьшить и так далее. Экспериментатор хотел бы установить, влияют ли какие-либо из этих изменений на результат производственного процесса. Наиболее очевидный подход в данном случае состоит в полном переборе комбинаций уровней интересующих факторов. Это отлично сработает, если бы число необходимых опытов в таком эксперименте не росло экспоненциально. Например, если вы хотите провести эксперимент с 7 факторами, то необходимое число опытов равно 2**7 = 128. Чтобы изучить 10 факторов вам потребуется 2**10 = 1,024 опытов. Поскольку для проведения каждого опыта нужна длительная и дорогостоящая перенастройка, то на практике часто нереально ставить столь большое число опытов. В этом случае при планировании эксперимента обычно используют дробные планы, отбрасывающие взаимодействия высокого порядка и уделяющие наибольшее внимание главным эффектам.
Построение плана
Подробное описание того, как строятся дробные факторные планы, выходит за пределы данного введения. Много интересного о 2**(k-p) планах можно найти, например, в работах Бейна и Рубина (1986), Бокса и Дрейпера (1987), Бокса, Хантера и Хантера (1978), Даниела (1976), Деминга и Моргана (1993), Мейсона, Ганста и Гесса (1989), Райана (1989), а также Монтгомери (1991) и многих других. В общем случае, программа успешно использует взаимодействия наивысших порядков для генерации новых факторов. В качестве примера рассмотрим следующий план, включающий 11 факторов, но требующий проведения только 16 опытов (наблюдений).| Design: 2**(11-7), Resolution III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Run | A | B | C | D | E | F | G | H | I | J | K |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 |
1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 |
1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 |
1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 |
1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 |
1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1 |
1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 |
1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1 |
1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1 |
1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 |
1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 |
Чтение плана. План, представленный в таблице, интерпретируется следующим образом. Каждый столбец таблицы содержит +1 или -1 для обозначения уровня соответствующего фактора (верхнего или нижнего, соответственно). Так, например, в первом опыте эксперимента все факторы от A до K установлены на верхнем уровне (+1); во втором опыте факторы A, B, и C - на верхнем уровне, а фактор D - на нижнем и так далее. Отметим также, что имеется множество опций для отображения плана на экране и сохранения в файле с использованием обозначений, отличных от ± 1 для уровней факторов. Например, можно использовать реальные значения факторов (например, 90° C и 100° C) или текстовые метки (Низкая температура, Высокая температура).
Рандомизация опытов. Поскольку многие условия проведения эксперимента могут измениться от опыта к опыту то, чтобы не возникали систематические смещения, следует рандомизировать порядок проведения опытов (модуль Планирование эксперимента позволяет случайно выбрать порядок их проведения).
Разрешение плана
План в приведенной выше таблице описывается как 2**(11-7) план разрешения III (три). Это означает, что изучается k = 11 факторов (первая цифра в скобках), однако p = 7 из этих факторов (вторая цифра в скобках) порождены взаимодействиями полного факторного плана 2**[(11-7) = 4]. В результате план не обеспечивает полного разрешения, т.е. имеются эффекты взаимодействий, которые смешиваются с другими эффектами (идентичны им). Вообще, план называется планом разрешения R, если в нем ни одно взаимодействие порядка l = 1,…,[(r+1)/2] не смешивается с каким-либо взаимодействием порядка меньше R-l. В данном примере, R равно 3. Ни одно из взаимодействий порядка l = 1 (то есть ни один главный эффект) не смешивается здесь с каким-либо другим взаимодействием порядка меньше R-l = 3-1 = 2. Главные эффекты в этом плане смешиваются со взаимодействиями 2-го порядка и, следовательно, все взаимодействия более высоких порядков также смешаны. Если провести 64 опыта по плану 2**(11-5), полученное разрешение равнялось бы четырем (R = IV). Для того чтобы сделать такой вывод достаточно убедиться, что взаимодействия порядка (l=1) (главные эффекты) не смешиваются со взаимодействиями порядка меньше R-l = 4-1 = 3, а взаимодействия второго порядка (l=2) не смешиваются со взаимодействиями порядка меньшего, чем R-l = 4-2 = 2. Это приводит к тому, что некоторые взаимодействия второго порядка в данном плане смешаны друг с другом.
Планы Плакетта - Бермана (матрица Адамара) для отсеивания
Если необходимо просеять большое число факторов, которые могут быть потенциально важными (т. е. связаны с интересующей нас зависимой переменной), хотелось бы использовать план, который бы позволил тестировать наибольшее число главных эффектов при наименьшем числе наблюдений, то есть построить план разрешения III с наименьшим числом наблюдений. Один из способов планирования такого эксперимента состоит в смешивании всех взаимодействий с “новыми” главными эффектами. Такие планы часто называют насыщенными, поскольку вся информация в них используется для оценки параметров, не оставляя степеней свободы для оценки эффекта (члена) ошибок ДА. Поскольку дополнительные факторы создаются приравниванием (“присвоением псевдонимов”, смотрите ниже) “новых факторов” к взаимодействиям в полной факторной модели, то эти планы всегда будут состоять из 2**k опытов, (то есть, 4, 8, 16, 32 и так далее опытов). Плакетт и Берман (Plackett и Burman, 1946) показали, как полная факторная модель может быть разбита так, чтобы получить насыщенные планы, в которых число опытов кратно 4, а не степени 2. Такие планы иногда называют планами с матрицей Адамара. Конечно, вы не обязаны использовать все имеющиеся факторы в этих планах, и фактически, иногда вам хотелось бы сгенерировать насыщенный план для еще одного фактора сверх тех, которые вы бы хотели тестировать. Это позволит оценить изменчивость случайных эффектов и тестировать оценки параметров на статистическую значимость.
Усиление разрешения плана методом инверсии
Одним из способов, с помощью которых разрешение III плана может быть усилено до разрешения IV, является метод инверсии (например, смотрите Box и Draper, 1987, Deming и Morgan, 1993). Предположим, что имеется 7-факторный план с 8 опытами:
| Design: 2**(7-4) design | |||||||
|---|---|---|---|---|---|---|---|
| Run | A | B | C | D | E | F | G |
| 1 2 3 4 5 6 7 8 |
1 1 1 1 -1 -1 -1 -1 |
1 1 -1 -1 1 1 -1 -1 |
1 -1 1 -1 1 -1 1 -1 |
1 1 -1 -1 -1 -1 1 1 |
1 -1 1 -1 -1 1 -1 1 |
1 -1 -1 1 1 -1 -1 1 |
1 -1 -1 1 -1 1 1 -1 |
| Design: 2**(7-4) design (+Foldover) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Run |
A |
B |
C |
D |
E |
F |
G |
New: H |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 |
1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 |
1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 |
1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 |
1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1 |
1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 |
1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1 |
1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 |
Псевдонимы для взаимодействий: генераторы плана
Вернемся к плану разрешения R = III. Теперь вы знаете, что главные эффекты плана смешаны с взаимодействиями 2-го порядка, и можете поставить вопрос: “Какие взаимодействия и какие главные эффекты смешаны?” Модуль Планирование эксперимента генерирует следующую таблицу.
| Factor |
Fractional Design Generators 2**(11-7) design (Factors are denoted by numbers) Alias |
|---|---|
| 5 6 7 8 9 10 11 |
123 234 134 124 1234 12 13 |
Подводя итоги, заметим, что коль скоро вы хотели бы включить меньше наблюдений (опытов) в ваш эксперимент, чем это требуется полным факторным планом 2**k, вы “жертвуете” эффектами взаимодействия и приписываете их некоторым уровням факторов. Получающийся план не является больше полным факторным, а становится дробным факторным.
Фундаментальное тождество. Другой способ описания генератора плана состоит в простом уравнении. Именно, если, например, фактор 5 в дробном факторном плане идентичен взаимодействию 123 (фактор 1 и фактор 2 и фактор 3), тогда, умножая кодированные значения взаимодействия 123 на кодированные значения фактора 5, мы получим в результате +1 (если все уровни факторов закодированы +1) или:
I = 1235
где символ I заменяет +1 (используя стандартные обозначения как, например, в Box и Draper, 1987). Так, мы знаем, что фактор 1 смешан с взаимодействием 235 , фактор 2 смешан с взаимодействием 123 , а фактор 3 смешан с взаимодействием 125, поскольку в каждом случае их произведение должно равняться 1. Смешанность взаимодействий 2-го порядка также определяется этим уравнением, поскольку взаимодействие 12, будучи умножено на взаимодействие 35, должно дать в результате 1 и, следовательно, они идентичны или смешаны. Поэтому можно суммировать все смешанные в плане эффекты с помощью подобного тождества, называемого фундаментальным тождеством.Разбиение на блоки
В некоторых производственных процессах изделия производятся “партиями” или блоками. Вам хотелось бы быть уверенными в том, что эти блоки не сдвинут (не сместят) оценки главных эффектов. Например, вы имеете печь для обжига специальной керамики, однако ее размеры ограничены, так что вы не можете проводить все опыты сразу. В этом случае вы разбиваете эксперимент на блоки. Однако вы не хотели бы опыты с положительными установками факторов проводить в одном блоке, а с отрицательными – в другом. Иначе случайные отличия между блоками будут систематически воздействовать на оценки главных эффектов интересующих нас факторов (другими словами, сместят их). В действительности вам хотелось бы так разбить опыты на блоки, чтобы любые различия между блоками (то есть блоковый фактор) не повлияли бы на результаты интересующих вас факторов. Это осуществляется введением блокового фактора как дополнительного фактора в плане эксперимента. Следовательно, вы “теряете” еще один эффект взаимодействия с блоковым фактором и получающийся план становится планом с меньшим разрешением. Однако такие планы часто имеют преимущество в мощности, т. к. позволяют оценивать и контролировать изменчивость производственного процесса, обусловленную различиями между блоками.
Повторение плана
Иногда желательно повторить (реплицировать) план, то есть провести опыт с каждой фиксированной комбинацией уровней факторов более одного раза. Это позволит оценить так называемую чистую ошибку эксперимента. Заметим, что при повторении плана можно вычислить изменчивость (изменчивость) измерений на каждой конкретной комбинации уровней факторов. Эта изменчивость даст представление о случайной ошибке измерений, (например, обусловленной неконтролируемыми факторами, ненадежностью инструментов измерений и так далее), поскольку повторные наблюдения совершаются при одинаковых условиях (установках уровней факторов). Такая оценка чистых ошибок может быть использована для оценки величины и статистической значимости вариации, обусловленной контролируемыми факторами.
Частные реплики. Если невозможно или нецелесообразно повторять все комбинации уровней (то есть проводить еще раз весь полный план), то можно все же получить оценку чистой ошибки при повторе только некоторых опытов. Однако нужно быть осторожным при рассмотрении смещений, потенциально возникающих при выборочном повторении только некоторых опытов. Если повторяются только те опыты, которые повторить легко, (например, собрать информацию в точках, где это дешевле всего), то можно случайно выбрать только те комбинации уровней факторов, в которых имеется очень маленькая (или очень большая) вариация, что приводит к недооценке (или переоценке) истинной величины чистой ошибки. Таким образом, нужно тщательно рассматривать, обычно основываясь на вашем представлении об изучаемом процессе, какие опыты следует повторять, то есть какие опыты дадут хорошую (несмещенную) оценку чистой ошибки.Добавление центральных точек (центроидов)
Планирование эксперимента для факторов, установленных на двух уровнях неявно предполагает, что их воздействие на зависимую переменную (например, на прочность ткани) линейно. При этом невозможно проверить, имеется ли нелинейная компонента (например, квадратичная) в соотношении между фактором A и зависимой переменной, коль скоро A оценивается только в двух точках (например, нижнем и верхнем уровнях). Если предполагается, что соотношение между факторами и зависимой переменной, скорее всего, нелинейно, то необходим один или несколько опытов, где все (непрерывные) факторы установлены в промежуточных (средних) точках. Такие опыты принято называть опытами в центральных точках (или просто в центрах), поскольку они в некотором смысле находятся в центре плана (смотрите график).
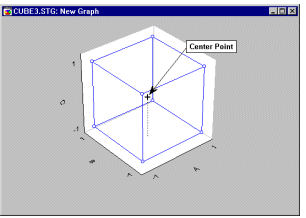
Позднее при анализе (смотрите ниже) можно сравнить измерения зависимой переменной в центральной точке со средним в остальных точках плана. Это дает возможность проверить нелинейность зависимостей (смотрите Box и Draper, 1987): Если среднее зависимой переменной в центре плана значительно отличается от общего среднего по всем остальным точкам плана, то это является основанием считать, что простое предположение о линейности связи факторов с зависимой переменной не выполняется.
Анализ результатов эксперимента 2**(k-p)
Дисперсионный анализ. Далее необходимо точно определить, какие факторы достоверно воздействуют на зависимую переменную. Например, в исследовании, приведенном Box и Draper (1987, стр. 115), хотелось бы знать, какие факторы, участвующие в производстве красителя, влияют на устойчивость краски. В этом примере, факторы 1 (Polysulfide – Полисульфид), 4 (Time – Время) и 6 (Temperature – Температура) значимо влияют на прочность ткани. Влияние остальных факторов незначимо. Заметим, что для простоты в таблице, приведенной ниже, показаны только главные эффекты.
| ANOVA; Var.:STRENGTH; R-sqr = .60614; Adj:.56469 (fabrico.sta) | |||||
|---|---|---|---|---|---|
| 2**(6-0) design; MS Residual =
3.62509 DV: STRENGTH |
|||||
| SS | df | MS | F | p | |
| (1)POLYSUFD (2)REFLUX (3)MOLES (4)TIME (5)SOLVENT (6)TEMPERTR Error Total SS |
48.8252 7.9102 .1702 142.5039 2.7639 115.8314 206.6302 524.6348 |
1 1 1 1 1 1 57 63 |
48.8252 7.9102 .1702 142.5039 2.7639 115.8314 3.6251 |
13.46867 2.18206 .04694 39.31044 .76244 31.95269 |
.000536 .145132 .829252 .000000 .386230 .000001 |
| ANOVA; Var.:STRENGTH; R-sqr = .58547; Adj:.56475 (fabrico.sta) | |||||
|---|---|---|---|---|---|
| 2**(3-0) design; MS Pure Error
= 3.594844 DV: STRENGTH |
|||||
| SS | df | MS | F | p | |
| (1)POLYSUFD (2)TIME (3)TEMPERTR Lack of Fit Pure Error Total SS |
48.8252 142.5039 115.8314 16.1631 201.3113 524.6348 |
1 1 1 4 56 63 |
48.8252 142.5039 115.8314 4.0408 3.5948 |
13.58200 39.64120 32.22154 1.12405 |
.000517 .000000 .000001 .354464 |
| Effect | Std.Err. | t (57) | p | |
|---|---|---|---|---|
| Mean/Interc. (1)POLYSUFD (2)REFLUX (3)MOLES (4)TIME (5)SOLVENT (6)TEMPERTR |
11.12344 1.74688 .70313 .10313 2.98438 -.41562 2.69062 |
.237996 .475992 .475992 .475992 .475992 .475992 .475992 |
46.73794 3.66997 1.47718 .21665 6.26980 -.87318 5.65267 |
.000000 .000536 .145132 .829252 .000000 .386230 .000001 |
Как видите, те же самые три фактора, которые были статистически значимыми, показывают наивысшие оценки параметров; так что установки этих трех факторов наиболее важны для окончательной прочности ткани.
Для анализа, включающего взаимодействия, интерпретация параметров эффектов несколько более сложная. Параметры двухуровневых взаимодействий определяются как полуразность между главными эффектами одного фактора на двух уровнях второго фактора (смотрите Mason, Gunst и Hess, 1989, стр. 127); подобным же образом, параметры трехфакторных взаимодействий определяются как полуразности между эффектами двухфакторного взаимодействия на двух уровнях третьего фактора и так далее.
Регрессионные коэффициенты. Можно также взглянуть на параметры модели регрессии (смотрите Множественная регрессия, том I). Чтобы продолжить пример, рассмотрим следующее уравнение прогноза:Strength = const + b1 *x1 +... + b6 *x6
Здесь x1 до x6 обозначают 6 анализируемых факторов. Таблица Effect Estimates - Оценки эффектов, показанная ранее, также содержит эти оценки параметров:
| Coeff. |
Std.Err. Coeff. |
-95.% Cnf.Limt |
+95.% Cnf.Limt |
|
|---|---|---|---|---|
| Mean/Interc. (1)POLYSUFD (2)REFLUX (3)MOLES (4)TIME (5)SOLVENT (6)TEMPERTR |
11.12344 .87344 .35156 .05156 1.49219 -.20781 1.34531 |
.237996 .237996 .237996 .237996 .237996 .237996 .237996 |
10.64686 .39686 -.12502 -.42502 1.01561 -.68439 .86873 |
11.60002 1.35002 .82814 .52814 1.96877 .26877 1.82189 |
| data file: FABRICO.STA [ 64
cases with 9 variables ] 2**(6-0) Design, Box & Draper, p. 117 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| POLYSUFD | REFLUX | MOLES | TIME | SOLVENT | TEMPERTR | STRENGTH | HUE | BRIGTHNS | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 . . . |
6 7 6 7 6 7 6 7 6 7 6 7 6 7 6 . . . |
150 150 170 170 150 150 170 170 150 150 170 170 150 150 170 . . . |
1.8 1.8 1.8 1.8 2.4 2.4 2.4 2.4 1.8 1.8 1.8 1.8 2.4 2.4 2.4 . . . |
24 24 24 24 24 24 24 24 36 36 36 36 36 36 36 . . . |
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 . . . |
120 120 120 120 120 120 120 120 120 120 120 120 120 120 120 . . . |
3.4 9.7 7.4 10.6 6.5 7.9 10.3 9.5 14.3 10.5 7.8 17.2 9.4 12.1 9.5 . . . |
15.0 5.0 23.0 8.0 20.0 9.0 13.0 5.0 23.0 1.0 11.0 5.0 15.0 8.0 15.0 . . . |
36.0 35.0 37.0 34.0 30.0 32.0 28.0 38.0 40.0 32.0 32.0 28.0 34.0 26.0 30.0 . . . |
| Regressn Coeff. |
Std.Err. |
t (57) |
p |
|
|---|---|---|---|---|
| Mean/Interc. (1)POLYSUFD (2)REFLUX (3)MOLES (4)TIME (5)SOLVENT (6)TEMPERTR |
-46.0641 1.7469 .0352 .1719 .2487 -.0346 .2691 |
8.109341 .475992 .023800 .793320 .039666 .039666 .047599 |
-5.68037 3.66997 1.47718 .21665 6.26980 -.87318 5.65267 |
.000000 .000536 .145132 .829252 .000000 .386230 .000001 |
Графические опции
Графики остатков. Вначале перед принятием конкретной “модели”, включающей конкретное число эффектов (например, главные эффекты для Polysulfide - Полисульфида, Time – Времени и Temperature – Температуры в текущем примере), нужно всегда проверить распределение величин остатков, которые вычисляются как разница между модельными (вычисленными на построенной модели) и наблюдаемыми значениями. Предоставляются опции для вычисления гистограмм таких остатков, а также для вероятностных графиков.
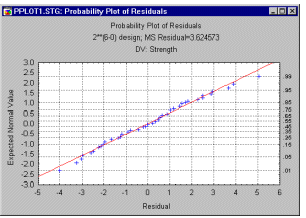

На этой диаграмме оценки эффектов ДА расположены по абсолютной величине значений: от наибольших к наименьшим. Величина каждого эффекта представлена столбиком, и часто столбики пересекают линией, указывающей, каков должен быть эффект по величине (то есть какова должна быть длина столбика), чтобы быть статистически значимым.
Нормальный график эффектов. Другим полезным, хотя и технически более сложным графиком, является нормальный вероятностный график. Как и в нормальной вероятностной диаграмме остатков, вначале оценки эффектов упорядочиваются по возрастанию, а затем вычисляются нормальные значения z, основываясь на предположении, что оценки распределены нормально. Эти значения z отмечаются на оси Y, а наблюдаемые оценки наносятся на оси X (как показано ниже).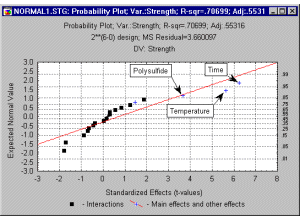

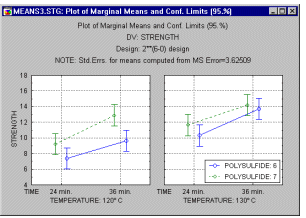
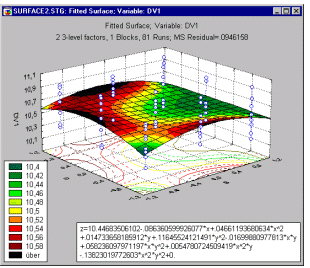
Типы таких диаграмм будут обсуждены позднее в данном разделе в связи с планами 3**(k-p), а также центральными композиционными планами и планами поверхности отклика.
Выводы
Планы 2**(k-p) наиболее часто используются в промышленности. Вклад большого числа факторов в производственный процесс может быть оценен относительно эффективно (т.е. с помощью небольшего числа опытов). Логика экспериментов такого рода весьма проста (каждый фактор имеет только два уровня), а с помощью модуля Планирование эксперимента построение плана и анализ таких экспериментов занимают буквально секунды.Недостатки. Простота этих планов является их главным недостатком. Как было отмечено ранее, основанием для использования двухуровневых факторов является убеждение в том, что изменения зависимой переменной (например, прочности ткани) линейны по своей природе. Часто это не выполняется, то есть многие переменные связаны с характеристиками качества нелинейным образом. В приведенном выше примере, если бы вы непрерывно увеличивали фактор температуры (существенно связанный с прочностью окраски ткани), то в конечном счете обнаружили бы “пик”, после которого прочность убывает при возрастании температуры. Этот тип нелинейности может быть обнаружен, если план содержит центральную точку. Нельзя точно подогнать нелинейную модель (например, квадратичную) с помощью планов 2**(k-p), однако, это можно сделать с помощью центральных композиционных планов.
Другим недостатком дробных планов является предположение о том, что взаимодействия высоких порядков отсутствуют, но иногда они действительно присутствуют. Например, если некоторые другие факторы установлены так, что оказывают отрицательное влияние на температуру. Однако в дробных факторных планах взаимодействия высоких порядков (выше двух), как правило, не будут обнаружены.
| В начало |
Дробные 2**(k-p) факторные планы часто используются в промышленных экспериментах, так как позволяют сокращать количество используемых данных. Предположим в качестве примера, что инженеру нужно изучить эффект воздействия на производственный процесс 11 переменных факторов, каждый из которых может быть установлен на 2 уровнях. Обозначим число факторов через k, в нашем примере это 11. Эксперимент с полным факторным планом, когда изучаются эффекты каждой комбинации уровней каждого фактора, будет требовать проведения 2**(k) опытов, или 2048 в нашем случае. Для уменьшения объема работ с данными инженер может решить отказаться от рассмотрения эффектов взаимодействий высоких порядков 11 факторов, и вместо этого сосредоточиться только на выявлении главных эффектов 11 факторов и некоторых эффектов взаимодействий низкого порядка, которые могут быть оценены с помощью эксперимента с меньшим, более разумным числом опытов. Существует другая, более теоретическая причина отказа от больших полных факторных 2-х уровневых экспериментов. Обычно нелогично заниматься идентификацией эффектов взаимодействий факторов эксперимента высоких порядков, игнорируя нелинейные эффекты низкого порядка, такие как квадратичные и кубические эффекты, которые не могут быть оценены, если используются только 2-х уровневые факторы. Таким образом, несмотря на то, что практические соображения часто приводят к необходимости экспериментов с малым числом опытов, это логически оправданно для таких экспериментов.
Альтернативой полного 2**k факторного плана является 2**(k-p) дробный факторный план, который требует только "часть" данных, необходимых для полного факторного плана. В нашем примере с k=11 факторами, если могут быть проведены только 64 опыта, может быть построен 2**(11-5) дробный факторный план для эксперимента с 2**6 = 64 опытами. В сущности, построен полный k - p = 6 факторный план эксперимента с уровнями p факторов, "построенных" по уровням выбранных взаимодействий высокого порядка других 6 факторов. Дробные факторные "жертвуют" эффектами взаимодействий высокого порядка, но эффекты низкого порядка, могут еще быть вычислены корректно. Однако могут быть использованы различные критерии для выбора взаимодействий высокого порядка, используемых в качестве генераторов, среди которых некоторые критерии иногда приводят к различным "лучшим" планам. Дробные 2**(k-p) факторные планы могут также содержать блоковые факторы. В некоторых производственных процессах изделия выпускаются "партиями" или блоками. Для того чтобы быть уверенным, что эти блоки не смещают ваши оценки эффектов k factors, блоковые факторы могут быть добавлены в план как дополнительные. Следовательно, вы можете "пожертвовать" дополнительными эффектами взаимодействий для создания блоковых факторов, но эти планы часто имеют большую мощность, т.к. позволяют оценивать и контролировать вариабельность (изменчивость) производственного процесса, вызванную блоковыми различиями.Критерий плана
Многие концепции, которые обсуждались в этом обзоре, также относятся и к разделу Обзор дробных 2**(k-p) факторных планов. Однако техническое описание построения дробных факторных планов выходит за рамки Вводного обзора. Детальные объяснения, как план 2**(k-p) эксперимента может быть найден, содержатся, например, у Bayne и Rubin (1986), Box и Draper (1987), Box, Hunter, и Hunter (1978), Montgomery (1991), Daniel (1976), Deming и Morgan (1993), Mason, Gunst, и Hess (1989), или Ryan (1989), и существует много других книг по этому предмету.Обычно опция Максимально несмешанные 2**(k-p) планы будет производить последовательный отбор, в зависимости от выбранного критерия поиска, с взаимодействиями высшего порядка в качестве генераторов для p факторов. Для примера рассмотрим следующий план, который включает 11 факторов, но требует только 16 опытов (наблюдений).
| Design: 2**(11-7), Resolution III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Run | A | B | C | D | E | F | G | H | I | J | K |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 |
1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 |
1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 |
1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 |
1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 |
1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1 |
1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 |
1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1 |
1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1 |
1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 |
1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 |
Критерий максимального разрешения плана. План, показанный в таблице результатов, характеризуется как 2**(11-7) план разрешения III (три). Это означает, что вы исследуете всего
k = 11 факторов, но p = 7 из них сгенерированы взаимодействиями полного 2**[(11-7) = 4] факторного плана. В результате этот план не дает полного разрешения, то есть существуют некоторые эффекты взаимодействий, смешанные с другими эффектами. В общем случае план имеет разрешение R, когда в нем нет взаимодействий порядка l, смешанных с любыми другими взаимодействиями порядка, меньшего R - l. В нашем примере R равно 3. Здесь нет взаимодействий порядка l = 1 (т.е. главных эффектов), смешанных с любыми другими взаимодействиями порядка меньшего, чем R - l = 3 -1 = 2. Поэтому главные эффекты в этом плане не смешаны друг с другом, но смешаны с двухфакторными взаимодействиями, а следовательно, и с другими взаимодействиями более высокого порядка. Очевидным, но тем не менее очень важным общим критерием плана является то, что взаимодействия высшего порядка, используемые как генераторы, должны быть выбраны так, чтобы план имел максимально возможное разрешение. Критерий максимальной несмешанности плана. Максимизация разрешения плана, однако, сама по себе не гарантирует, что выбранные генераторы дают "лучший" план. Для примера рассмотрим два различных плана с разрешением IV. В обоих планах главные эффекты могут быть несмешанными друг с другом, и 2-х факторные взаимодействия могут быть несмешанными с главными эффектами, т.е не существует взаимодействий порядка l = 2, смешанных с любыми другими взаимодействиями порядка меньшего, чем R - l = 4 - 2 = 2. Оба плана могли быть различными, однако, по отношению к степени смешивания 2-факторных взаимодействий. Для планов с разрешением IV "критическим порядком", при котором появляется смешивание эффектов, является 2-факторные взаимодействия. В одном плане не "критического порядка" 2-факторные взаимодействия могут быть несмешанными со всеми другими 2-факторными взаимодействиями, в то время как в другом плане фактически все 2-факторные взаимодействия могут быть несмешанными со всеми другими 2-факторными взаимодействиями. Второй план – это план "почти разрешения V" может быть более предпочтительнее, чем план "просто точно разрешения IV". Это означает, что даже несмотря на то, что главным критерием являлся критерий максимального разрешения, может быть введен дополнительный критерий, по которому выбираются те генераторы, содержащие максимальное число взаимодействий порядка меньшего или равного критическому, для данного разрешения, несмешанных со всеми другими взаимодействиями критического порядка. Этот критерий называется критерием максимальной несмешанности, иначе говоря, дополнительным критерием плана при поиске 2**(k-p) плана. Критерий минимальной аберрации плана. Критерий минимальной аберрации плана является другим необязательным критерием, используемым при поиске 2**(k-p) плана. В некоторых отношениях этот критерий похож на критерий максимальной несмешанности. Формально план с минимальной аберрацией определяется как план с максимальным разрешением "с минимальным числом слов в определяющем взаимоотношении, которое имеет минимальную длину" (Fries & Hunter, 1984). Менее формально, действие критерия основано на выборе генераторов, которые дают наименьшее число пар смешанных взаимодействий критического порядка. Например, план разрешения IV с минимальной аберрацией имел бы минимальное число пар смешанных 2-факторных взаимодействий.Для пояснения различия между критериями максимальной несмешанности и минимальной аберрации рассмотрим максимально несмешанный план 2**(9-4) и план 2**(9-4) с минимальной аберрацией, как в примере, данном Box, Hunter, и Hunter (1978). Если вы сравните эти два плана, вы увидите, что в максимально несмешанном плане 15 из 36 2-факторных взаимодействий не смешаны с любыми другими 2-факторными взаимодействиями, в то время как в плане с минимальной аберрацией только 8 из 36 2-факторных взаимодействий не смешаны с любыми другими 2-факторными взаимодействиями. План с минимальной аберрацией, однако, дает 18 пар смешанных взаимодействий, в то время как максимально несмешанный план дает 21 пару смешанных взаимодействий. Таким образом, эти критерии приводят к выделению генераторов, дающих различные "лучшие" планы.
К счастью, выбор между критерием максимальной несмешанности и критерием минимальной аберрации не вносит различия в выбранном плане (за исключением, возможно, переобозначения факторов), когда имеется 11 или меньше факторов, - единственное исключение составляет план 2**(9-4), описанный выше (смотрите Chen, Sun, & Wu, 1993). Для планов с более чем 11 факторами оба критерия приводят к весьма различным планам, и нет лучшего совета, как использовать оба критерия, а затем сравнить полученные планы и выбрать план, наиболее отвечающий вашим потребностям. Добавим, что максимизация числа полностью несмешанных эффектов часто имеет больший смысл, чем минимизация числа пар смешанных эффектов.Выводы
Дробные 2**(k-p) факторные планы, вероятно, наиболее часто используемые планы в промышленных экспериментах. Предмет рассмотрения любого
2**(k-p) дробного факторного эксперимента включает число исследуемых факторов, число опытов в эксперименте и наличие блоков опытов эксперимента. После этих основных вопросов следует также определить, позволяет ли число опытов найти план требуемого разрешения и степень смешивания для критического порядка взаимодействий, для данного разрешения.| В начало |
В некоторых случаях приходиться анализировать факторы, имеющие более 2-х уровней. Например, если предполагается, что влияние факторов на зависимую переменную не линейное, то необходимо, как говорилось ранее (см. 2**(k-p) планы), по меньшей мере, 3 уровня для проверки линейных и квадратичных эффектов (и взаимодействий). Более того, некоторые факторы могут быть категориальными с более чем двумя категориями. Например, вы можете иметь три различных машины, производящие конкретную деталь.
Планирование экспериментов 3**(k-p)
Общий механизм построения дробных факторных планов на трех уровнях (планов 3**(k-p)) очень схож с тем, который описан для 2**(k-p) планов. Именно, отправляясь от полного факторного плана, взаимодействия используются для построения “новых” факторов (или блоков) с помощью определения их уровней равными соответствующим членам взаимодействий (то есть, определяя новые факторы как псевдонимы взаимодействий).
Например, рассмотрим следующий простой факторный план 3**(3-1):
| 3**(3-1) fractional factorial design, 1 block , 9 runs |
|||
|---|---|---|---|
| Standard Run |
A |
B |
C |
| 1 2 3 4 5 6 7 8 9 |
0 0 0 1 1 1 2 2 2 |
0 1 2 0 1 2 0 1 2 |
0 2 1 2 1 0 1 0 2 |
C = 3 - mod3 (A+B)
Здесь символ mod3(x) обозначает сравнение по модулю 3 (остаток от деления x на 3). Например, mod3(0) равен 0, mod3(1) равен 1, mod3(3) равен 0, mod3(5) равен 2 (3 – наибольшее число, не большее 5, делящееся на 3; так что окончательно, 5-3=2) и так далее.Фундаментальное тождество. Если вы примените эту функцию к сумме столбцов A и B в таблице, показанной выше, вы получите третий столбец C. Аналогично планам 2**(k-p) (см. 2**(k-p) планы для обсуждения понятия фундаментальное тождество в связи с планами 2**(k-p)), это смешивание взаимодействий с “новыми” главными эффектами может быть представлено выражением:
0 = mod3 (A+B+C)
Если вы снова взгляните на таблицу плана 3**(3-1), показанную ранее, вы увидите, что, на самом деле, если вы просуммируете числа в трех столбцах, они дадут в результате 0, 3 или 6, то есть значения, делящиеся на 3 без остатка (и, следовательно, mod3(A+B+C)=0). Или кратко ABC=0, для окончательного выражения смешивания факторов в дробном плане 3**(k-p).Некоторые из планов будут иметь фундаментальные тождества, содержащие множитель 2, например,
0 = mod3 (B+C*2+D+E*2+F)
Это обозначение можно интерпретировать, как и прежде, то есть оператор деления по модулю3 для суммы B+2*C+D+2*E+F должен быть равен 0. Следующий пример демонстрирует данное тождество.Пример плана 3**(4-1) в 9 блоках
Здесь приведены результаты для 4-х факторного 3-х уровневого дробного факторного плана в 9 блоках, требующего только 27 опытов.
SUMMARY: 3**(4-1) fractional factorial
Design generators: ABCD
Block generators: AB,AC2
Number of factors (independent variables): 4
Number of runs (cases, experiments): 27
Number of blocks: 9
| Unconfounded Effects (experi3.sta) | ||
|---|---|---|
| EXPERIM. DESIGN |
List of uncorrelated factors and
interactions 3**(4-1) fractional factorial design, 9 blocks, 27 runs |
|
| Unconf. Effects (excl. blocks) |
Unconfounded if blocks included? |
|
| 1 2 3 4 5 6 7 8 |
(1)A (L) A (Q) (2)B (L) B (Q) (3)C (L) C (Q) (4)D (L) D (Q) |
Yes Yes Yes Yes Yes Yes Yes Yes |
Планы Бокса-Бенкена
Для планов 2**(k-p) Plackett и Burman (1946) разработали метод для отсеивания максимального числа (главных) эффектов при возможно меньшем числе опытов. Эквивалентом для планов 3**(k-p) являются так называемые планы Бокса-Бенкена (Box и Behnken, 1960; смотрите также Box и Draper, 1984). Эти планы не имеют простых генераторов (конструируются комбинированием двухуровневых факторных планов с планами неполных блоков) и имеют сложную смесь взаимодействий. Тем не менее, они экономичны, и, следовательно, особенно полезны в случаях, когда дорого проводить необходимые опыты.
Анализ плана 3**(k-p)
Анализ таких типов планов происходит, в основном, таким же образом, как и анализ, описанный для планов 2**(k-p) планы. Однако для каждого эффекта теперь можно тестировать его линейность или квадратичность (нелинейность). Например, при изучении выхода химического процесса, температура может влиять на него нелинейным образом, то есть максимум выхода достигается при температуре, установленной на среднем уровне. Так, нелинейность часто возникает, если процесс находится вблизи оптимального уровня.Дисперсионный анализ
Чтобы оценить параметры ДА, уровни факторов, находящихся в анализе, специально перекодированы так, чтобы можно было тестировать линейные и квадратичные компоненты соотношений между факторами и зависимой переменной. Так, независимо от исходной метрики установки факторов (например, 100° C, 110° C, 120° C), программа всегда перекодирует эти значения в -1, 0, и +1 для вычислений. Получающиеся оценки параметров ДА могут интерпретироваться аналогично оценкам параметров планов 2**(k-p).
Например, рассмотрим следующую таблицу результатов ДА:
| Factor | Effect | Std.Err. | t (69) | p |
|---|---|---|---|---|
| Mean/Interc. BLOCKS(1) BLOCKS(2) (1)TEMPERAT (L) TEMPERAT (Q) (2)TIME (L) TIME (Q) (3)SPEED (L) SPEED (Q) 1L by 2L 1L by 2Q 1Q by 2L 1Q by 2Q |
103.6942 .8028 -1.2307 -.3245 -.5111 .0017 .0045 -10.3073 -3.7915 3.9256 .4384 .4747 -2.7499 |
.390591 1.360542 1.291511 .977778 .809946 .977778 .809946 .977778 .809946 1.540235 1.371941 1.371941 .995575 |
265.4805 .5901 -.9529 -.3319 -.6311 .0018 .0056 -10.5415 -4.6812 2.5487 .3195 .3460 -2.7621 |
0.000000 .557055 .343952 .740991 .530091 .998589 .995541 .000000 .000014 .013041 .750297 .730403 .007353 |
На практике, а также с точки зрения “интерпретируемости результатов” обычно пытаются избежать квадратичных взаимодействий. Например, квадратично-квадратичное взаимодействие факторов A и B указывает на то, что нелинейные эффекты фактора A изменяются нелинейным образом (модифицируются) при установках фактора B. Это означает, что имеется довольно сложное взаимодействие факторов, так что становится трудно понять и оптимизировать процесс. Иногда проблему можно решить с помощью подходящего нелинейного преобразования (например, логарифмирования log) зависимой переменной.
Центрированные и нецентрированные полиномы. Как уже упоминалось ранее, простая интерпретация оценок эффектов применима только в случае, если использовалась параметризация модели по умолчанию. В этом случае программа кодирует квадратичные взаимодействия факторов так, чтобы они становились максимально “несвязанными” с линейными главными эффектами.
Графическое представление результатов
Имеются те же диаграммы (например, диаграммы остатков) для планов 3**(k-p), что и для 2**(k-p) планов. Таким образом, перед интерпретацией окончательных результатов следует всегда вначале посмотреть на распределение остатков модели. Заметим, что ДА предполагает нормальное распределение остатков (ошибок).
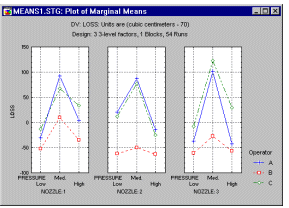
Диаграммы взаимодействия средних. Если взаимодействуют категориальные факторы (например, тип машины, оператор или регулировка), то наилучший способ понять взаимодействия - просмотреть диаграммы маргинальных средних для взаимодействий.

Планы для факторов на 2-х и 3-х уровнях
Вы можете также генерировать стандартные планы для факторов на 2-х и 3-х уровнях. Точнее, вы можете создавать стандартные планы, перечисленные Кантором и Янгом для Национального бюро стандартов США (смотрите McLean и Anderson, 1984). Детали используемого метода построения плана лежат за пределами этого введения. В некотором смысле, техника является комбинацией процедур, описанных для планов 2**(k-p) и 3**(k-p). Следует отметить, что хотя все эти планы очень эффективны, они не обязательно ортогональны. Модуль Планирование эксперимента использует общий алгоритм оценки параметров ДА и сумм квадратов, который не требует ортогональности плана.
Планирование и анализ таких экспериментов лежит в русле обсуждений для экспериментов 2**(k-p) планов и 3**(k-p).
| В начало |
Центральные композиционные планы и нефакторные планы для поверхности отклика
Планы 2**(k-p) и 3**(k-p) требуют, чтобы факторы устанавливались, например, на 2-х или 3-х уровнях. Во многих примерах такие планы невозможны в силу неосуществимости некоторых комбинаций факторов по тем или иным причинам (например, когда факторы A и B не могут быть установлены на верхних уровнях одновременно). Помимо этого, по причинам, связанным с эффективностью, которые будут кратко обсуждены далее, часто желательно исследовать интересующую нас экспериментальную область в конкретных точках, которые не могут быть представлены в факторном плане.Все планы, обсуждаемые в данном разделе, посвящены оценке (подгонке) поверхностей отклика, удовлетворяющих общему уравнению (модели):
y = b0 +b1 *x1 +...+bk *xk + b12 *x1 *x2 +b13 *x1 *x3 +...+bk-1,k *xk-1 *xk + b11 *x1? +...+bkk *xk?
Иными словами, подгоняется модель для наблюдаемых значений зависимой переменной y, которая включает (1) главные эффекты факторов x1 , ..., xk, (2) их взаимодействия (x1*x2, x1*x3, ... ,xk-1*xk) и (3) их квадратичные компоненты (x1**2, ..., xk**2). Не делается никаких предположений относительно “уровней” факторов; вы можете анализировать любой набор непрерывных значений факторов.Имеются некоторые соображения, касающиеся эффективности и несмещенности плана, которые приводят к стандартным планам, обычно используемым для подгонки поверхностей отклика, и эти стандартные планы будут коротко обсуждены (например, смотрите Box, Hunter и Hunter, 1978; Box и Draper, 1987; Khuri и Cornell, 1987; Mason, Gunst и Hess, 1989; Montgomery, 1991). Однако, как будет показано ниже при рассмотрении планов для поверхностей с ограничениями, а также D- и A-оптимальных планов, иногда эти стандартные планы не могут быть использованы по практическим соображениям. Повторим, однако, что опции анализа центральных композиционных планов не требуют никаких предположений относительно структуры массива данных, то есть относительно числа различных значений фактора или их комбинаций по опытам эксперимента и, следовательно, эти опции могут использоваться для анализа любого типа плана для подгонки к данным общей модели, описанной выше.
Соображения относительно плана
Ортогональные планы. Одной желательной характеристикой любого плана является независимость оценок главных эффектов и взаимодействий интересующих нас факторов. Например, предположим, что вы имеете двухфакторные эксперименты с факторами на двух уровнях. Ваш план состоит из четырех опытов:
| A | B | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 |
1 1 -1 -1 |
1 1 -1 -1 |
Чтобы оценить независимые вклады двух факторов, их уровни в четырех опытах должны быть установлены так, чтобы “столбцы” плана были независимыми друг от друга. Другими словами, столбцы матрицы плана (а их столько, сколько имеется параметров главных эффектов и взаимодействий, которые желательно оценить) должны быть ортогональными. Например, если план организован следующим образом:
| A | B | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 |
1 1 -1 -1 |
1 -1 1 -1 |
Два столбца матрицы плана ортогональны, если сумма произведений их элементов равна нулю (иными словами, равно нулю их скалярное произведение). На практике часто возникают ситуации, когда, например, из-за потери некоторых данных или по другим причинам столбцы матрицы плана не полностью ортогональны. Общее правило здесь состоит в том, что чем более столбцы ортогональны, тем план лучше организован, тем больше информации относительно интересующих нас эффектов может быть извлечено. Поэтому одним из соображений при выборе стандартных центральных композиционных планов является нахождение планов, которые ортогональны или почти ортогональны.
Ротатабельные планы. Второе соображение состоит в том, что нужно делать, чтобы наилучшим образом извлечь максимальное количество (несмещенной) информации из плана. Не вдаваясь в подробности (смотрите монографии Box, Hunter и Hunter, 1978; Box и Draper, 1987, глава 14; смотрите также Deming и Morgan, 1993, глава 13), можно показать, что стандартная ошибка предсказания значений зависимой переменной пропорциональна
(1 + f(x)' * (X'X)?? * f(x))**?
где f(x) обозначает эффекты факторов соответствующей модели (f(x) - вектор, а f(x)' - транспонированный вектор f(x)), X - матрица плана; а X'X**-1 – матрица, обратная ковариационной матрице X'X. Deming и Morgan (1993) называют это выражение нормализованной неопределенностью, эту функцию также называют дисперсионной функцией (смотрите определение в Box и Draper (1987)). Количество неопределенности в предсказании значений зависимой переменной зависит от вариабельности точек плана и их ковариаций между опытами. (Заметим, что эта величина обратно пропорциональна определителю матрицы X'X; данный вопрос будет далее обсуждаться в разделе D- и A-оптимальных планов). Очевидно, желательно выбрать план таким образом, чтобы извлечь наибольшую информацию о зависимой переменной и получить наименьшую неопределенность для прогноза ее будущих значений. Из приведенного выражения следует, что количество информации (или нормализованной информации согласно Deming и Morgan, 1993) обратно пропорционально нормализованной неопределенности.Для простого ортогонального плана с 4-мя опытами, приведенного ранее, информационная функция равна
Ix = 4/(1 + x1? + x2?)
где x1 и x2 обозначают соответственно уровни факторов A и B, (смотрите Box и Draper, 1987).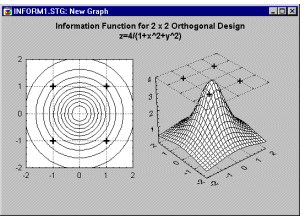
Чтобы оценить нелинейные компоненты (квадратичные, второго порядка) соотношений между факторами и зависимой переменной, необходимо иметь, по крайней мере, 3 уровня соответствующих факторов. Как же выглядит информационная функция для простого факторного плана 3-на-3 в квадратичной модели (второго порядка), показанной в начале данного раздела?
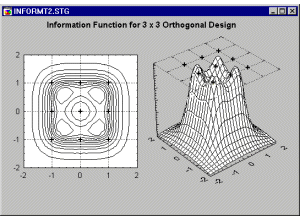
Известно (см. Box и Draper, 1987 или Montgomery, 1991), что эта функция выглядит более сложно, содержит “карманы” с высокой плотностью в угловых областях (которые, вероятно, представляют малый интерес для экспериментатора) и, очевидно, не является постоянной на окружностях. Следовательно, она не ротатабельна. Это означает, что при различных вращениях точек плана будет извлекаться разное количество информации.
Звездные точки и ротатабельные планы второго порядка. Можно показать, что при добавлении так называемых звездных точек к простым (квадратным или кубическим) 2-уровневым факторным планам можно получить ротатабельные, а иногда и ортогональные или почти ортогональные планы. Например, к ротатабельному плану приводит добавление следующего ряда точек к простому ортогональному плану 2-на-2:| A | B | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 Run 5 Run 6 Run 7 Run 8 Run 9 Run 10 |
1 1 -1 -1 -1.414 1.414 0 0 0 0 |
1 -1 1 -1 0 0 -1.414 1.414 0 0 |
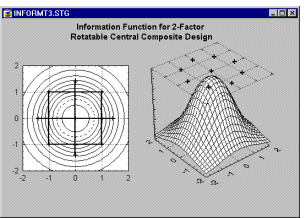
Информационная функция этого плана для модели второго порядка (квадратичной модели) ротатабельна, т. е. постоянна на окружностях с центром в начале координат (иными словами, план стал ротатабельным).
Альфа для ротатабельности и ортогональности
Две характеристики плана – ортогональность и
ротатабельность – зависят от числа центральных
точек плана и так называемого осевого
расстояния![]() a (альфа), которое равно расстоянию от
звездных точек до центра плана (т. е. 1.414 для
плана, показанного выше). Можно показать, (см.
например, Box, Hunter, и Hunter, 1978; Box и Draper, 1987, Khuri и Cornell,
1987; Montgomery, 1991), что план ротатабелен, если:
a (альфа), которое равно расстоянию от
звездных точек до центра плана (т. е. 1.414 для
плана, показанного выше). Можно показать, (см.
например, Box, Hunter, и Hunter, 1978; Box и Draper, 1987, Khuri и Cornell,
1987; Montgomery, 1991), что план ротатабелен, если:
![]() = ( nc
)?
= ( nc
)?
Центральный композиционный план является ортогональным, если выбрать альфа так, чтобы:
![]() = {[( nc
+ ns + n0 )? - nc?]? * nc/4}?
= {[( nc
+ ns + n0 )? - nc?]? * nc/4}?
где
nc число кубических точек
плана
ns число звездных точек
плана
n0 число центральных точек
плана
n0 ![]() 4*nc? + 4 - 2k
4*nc? + 4 - 2k
Наконец, если имеется разбиение на блоки, Box и Draper (1987) дают следующую формулу осевого (аксиального) расстояния для достижения ортогональности, и (в большинстве случаев) также для получения приемлемых контуров информационной функции, т. е. контуров, близких к сферическим:
![]() = [k*(l+ns0/ns)/(1+nc0/nc)]?
= [k*(l+ns0/ns)/(1+nc0/nc)]?
где
ns0 число центральных
точек в звездной части плана
ns число нецентральных
звездных точек плана
nc0 число центральных
точек в кубической части плана
nc число нецентральных
точек кубических точек плана
Доступные стандартные планы
Стандартные центральные композиционные планы обычно строятся следующим образом: в качестве кубической части плана берется план 2**(k-p) и затем он дополняется звездными и центральными точками. Box и Draper (1987) перечислили ряд таких планов.
Малые композиционные планы. В стандартных планах кубическая часть обычно является планом разрешения V (или выше). Это, однако, не является обязательным, и в случаях, когда опыты дороги, или когда необходимо построить статистически наиболее мощный тест для проверки адекватности модели, можно выбрать кубическую часть планов с разрешением III. Например, это можно сделать с помощью планов Плакетта-Бермана. Hartley (1959) описал такие планы.
Анализ центральных композиционных планов
Анализ центральных композиционных планов во многом подобен анализу 3**(k-p) планов. Программа подгоняет данные с помощью общей модели, описанной ранее; например, для двух переменных программа будет подгонять модель:
y = b0 + b1*x1 + b2*x2 + b12*x1*x2 + b11*x12 + b22*x22
Подогнанная поверхность отклика
Форму подогнанной поверхности отклика лучше всего представить в графическом виде, и вы можете строить как контурные диаграммы, так и диаграммы поверхности отклика (смотрите пример ниже).
Категоризованные поверхности отклика
Вы можете подогнать 3-х мерную поверхность к вашим данным, категоризованную по некоторым другим переменным. Например, если стандартный центральный композиционный план повторен 4 раза, очень полезно посмотреть, насколько подобны поверхности, получающиеся при подгонке в каждой реплике.
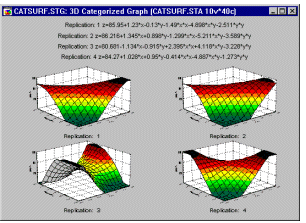
Графическое представление позволит вам убедиться в надежности результатов, а также выявить области, в которых имеются отклонения.
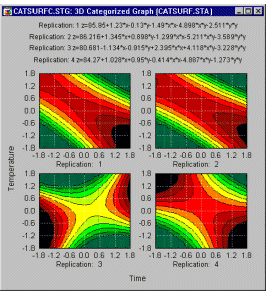
Очевидно, третья реплика дает поверхность, отличную от других. В репликах 1, 2 и 4 подогнанные поверхности очень похожи друг на друга. Таким образом, необходимо выяснить, что является причиной этого заметного отличия в третьей реплике плана.
| В начало |
Планы латинских квадратов используются в тех случаях, когда интересующие нас факторы имеют более двух уровней, и вы заранее знаете, что между факторами нет взаимодействий (или этими взаимодействиями можно пренебречь). Например, если вы хотите проверить воздействие 4 топливных присадок на снижение концентрации окиси азота и имеете в своем распоряжении 4 автомобиля и 4 водителя, то в принципе, можно поставить полный факторный эксперимент 4 x 4 x 4, который требует 64 опыта. Однако вас реально не интересуют (малые) взаимодействия между топливными присадками и водителями, топливными присадками и автомобилями, а также автомобилями и водителями. Больше всего вас интересует оценка главных эффектов, в особенности фактор топливных присадок. В то же время хотелось бы иметь уверенность, что главные эффекты водителей и автомобилей не влияют на оценку главного эффекта топливных присадок (не смещают их).
Если вы обозначите присадки буквами A, B, C и D, то план латинских квадратов, который позволит получить оценки несмешанных главных эффектов, выглядит следующим образом (смотрите также Box, Hunter и Hunter, 1978, стр. 263):| Car | ||||
|---|---|---|---|---|
| Driver | 1 | 2 | 3 | 4 |
| 1 2 3 4 |
A D B C |
B C D A |
D A C B |
C B A D |
Пример, показанный выше, на самом деле является лишь одним из трех возможных расположений уровней факторов, позволяющих получить несмещенные оценки главных эффектов. Такое расположение факторов называется Латинским квадратом. Выше показан латинский квадрат 4 x 4. Вместо требующихся в полном факторном эксперименте 64 опытов достаточно выполнить только 16.
Греко-латинские квадраты. Замечательное свойство латинских квадратов состоит в том, что они могут накладываться друг на друга, образуя Греко-латинские квадраты. Например, следующие два латинских квадрата 3 x 3 могут быть преобразованы в греко-латинский квадрат:
![]()
Гипер-греко-латинские квадраты. Для некоторого числа уровней имеется более двух возможных расположений в латинские квадраты. Например, существует три различных латинских квадрата на 4-х уровнях. Если их наложить друг на друга, получится план Гипер-греко-латинских квадратов. С его помощью можно оценить главные эффекты всех пяти 4-уровневых факторов, проведя эксперимент только с 16 опытами.
Анализ плана
Анализ планов латинских квадратов прост. Кроме того, могут быть получены диаграммы средних для интерпретации результатов.Очень большие планы, случайные эффекты, несбалансированные вложения
Заметим, что имеется несколько методов, которые также позволяют проводить анализ такого типа планов; обращайтесь к разделу Методы дисперсионного анализа для подробностей. В частности, в разделе Компоненты дисперсии и смешанная модель ANOVA/ANCOVA описаны весьма эффективные методы для анализа планов с несбалансированными вложениями (когда вложенные факторы имеют другие уровни внутри уровней факторов, в которые они вложены), очень больших вложенных планов (например, с более чем 200 уровнями в совокупности) или иерархически вложенных планов (включая или исключая случайные эффекты).| В начало |
Приложения. Методы Тагучи находят все большее применение в последние годы. Примеры значительного улучшения качества, связанного с внедрением этих методов (смотрите, например, Phadke, 1989; Noori, 1989), вызвали интерес к ним американских промышленников. Так, некоторые из ведущих производителей начали использовать их с очень большим успехом. Например, AT&T использует эти методы в производстве очень больших интегральных контуров (ОБИК), компания Форд добилась значительного улучшения качества, используя эти методы (Американский институт снабжения, 1984 по 1988).
Обзор. Методы Тагучи находятся во многих отношениях в стороне от традиционных процедур контроля качества (смотрите Контроль качества и Анализ производственных процессов) и промышленного эксперимента. Особенно важными являются следующие понятия:
Эти основные аспекты методов робастного планирования будут обсуждаться в следующих разделах. По этим методам недавно было опубликовано несколько монографий, например, Peace (1993), Phadke (1989), Ross (1988) и Roy (1990), и рекомендуется обращаться к ним для более детального изучения темы. Вводные обзоры идей Тагучи о качестве и его улучшении можно найти в работах Barker (1986), Garvin (1987), Kackar (1986) и Noori (1989).
Функции качества и потерь качества
Что такое качество. Тагучи начинает с вопроса, что такое качество? Нелегко дать простое определение качества; однако, если ваш новый автомобиль теряет скорость в центре напряженного перекрестка, подвергая вас и других участников движения риску, то вы говорите, что ваш автомобиль не обладает высоким качеством. Понятие противоположное качеству более простое: это общие потери для вас и для общества, обусловленные функциональной изменчивостью (изменчивостью) и неблагоприятными побочными эффектами, связанными с соответствующим продуктом. Таким образом, в качестве рабочего определения вы можете измерять качество в терминах этих потерь, и чем больше потери качества, тем ниже оно само.
Разрывная функция потерь. Вы можете сформулировать гипотезу об общем классе и форме функции потерь. Предположим, что имеется особая идеальная точка высшего качества; например, превосходный автомобиль без каких-либо проблем с качеством. Обычно в статистическом контроле процессов (СКП, см. также Анализ производственных процессов) принято определять уровень допуска вокруг номинальной идеальной точки производственного процесса. Согласно традиционной точке зрения, используемой в методах СКП, если вы находитесь внутри допуска, у вас не возникает проблем с качеством. Другими словами, внутри зоны допуска потери качества равны нулю. Если вы вышли за его пределы, потери качества объявляются неприемлемыми. Так, согласно традиционной точке зрения, функция потерь качества является разрывной порогообразной функцией: если вы находитесь внутри зоны допуска, потери качества пренебрежимы, а когда вы выходите за его пределы, потери становятся неприемлемыми.
Квадратичная функция потерь. Зададимся вопросом: является ли кусочно-постоянная функция хорошей моделью для потери качества? Вернемся к примеру “превосходного автомобиля”. Имеется ли разница между автомобилем, с которым ничего не случилось в течение года после покупки, и автомобилем, у которого начало что-то немножко барахлить, например, отвалились некоторые крепления и разбились часы на панели (все это входит в гарантийный ремонт, не так ли...)? Если вы когда-либо покупали новый автомобиль, вы очень хорошо знаете, как могут раздражать такие небольшие по общему признанию проблемы с качеством. Точка зрения здесь такова: не является реалистичным предположение о том, что если вы удаляетесь от номинального определения вашего производственного процесса, потери качества равны нулю, если вы находитесь в зоне допуска. Наоборот, если вы не попали точно “в цель”, то потери все же существуют, например, в терминах удовлетворения покупателя. Более того, эти потери, вероятно, не являются линейной функцией отклонения от номинальной спецификации процесса, а являются квадратичной функцией арочного типа (вроде перевернутой буквы U). Шум в одном месте вашего автомобиля раздражает, но вы, вероятно, не будете слишком опечалены этим; но добавьте еще пару шумов и, возможно, вы объявите ваш автомобиль “хламом”. Если постепенные отклонения от номинала дают непропорциональное увеличение потерь, то скорее всего это квадратичные увеличения.
Вывод: контроль изменчивости. Если фактически потери качества являются квадратичной функцией отклонения от номинального значения, то цель ваших усилий состоит в том, чтобы минимизировать квадрат отклонения или дисперсию продукта относительно его номинальной (идеальной) спецификации, а не число единиц внутри границы допуска (как это делается в традиционных процедурах анализа процессов).
Отношения (С/Ш) сигнал/шум
Измерение потери качества. Даже если вы заключили, что функция потерь квадратична, вы до сих пор точно не знаете, как измерять сами потери. Однако, на какой бы мере вы ни остановились, она должна отражать квадратичную природу функции.
Сигнал, шум и управляющие факторы. Продукт идеального качества всегда должен откликаться одинаковым образом на управляющие сигналы. Когда вы поворачиваете ключ зажигания автомобиля, то ожидаете, что стартер провернет двигатель, и он заведется. В автомобиле идеального качества процесс зажигания всегда происходит одним и тем же образом, например, после трех поворотов ключа зажигания двигатель заводится. Если в ответ на один и тот же сигнал - поворот ключа зажигания - наблюдается случайная изменчивость процесса, вы имеете дело с качеством, худшим, чем идеальное. Например, из-за таких неконтролируемых факторов, как низкая температура, влажность, изношенность двигателя и так далее последний может иногда завестись только после 20 попыток и даже не завестись совсем. Этот пример иллюстрирует ключевой принцип измерения качества по Тагучи: вам хотелось бы минимизировать изменчивость реакции продукта в ответ на факторы шума, максимизируя при этом изменчивость в ответ на управляющие факторы.
Факторы Шума - это те факторы, которые находятся вне контроля оператора. В примере с автомобилем эти факторы включают колебания температуры, различия в качестве бензина, изношенность двигателя и так далее. Управляющие факторы – это те факторы, которые устанавливаются или управляются оператором машины для ее использования по назначению (поворот ключа зажигания запускает двигатель и автомобиль может начать движение).
Итак, целью ваших усилий по улучшению качества является установка наилучших значений управляющих факторов, которые включены в производственный процесс для того, чтобы максимизировать отношение С/Ш (сигнал-шум); так что здесь факторы в эксперименте выступают как управляющие.
С/Ш отношения. Вывод из предыдущего состоит в том, что качество может быть рассмотрено с точки зрения отклика продукта на шумы и управляющие факторы. Идеальный продукт будет реагировать только на сигналы оператора, и не будет реагировать на случайный шум (погоду, температуру, влажность и так далее). Следовательно, цель ваших усилий по совершенствованию качества может рассматриваться как попытка максимизировать отношение сигнал/шум (С/Ш) соответствующего продукта. Отношения С/Ш, описанные в последующих параграфах, были предложены Тагучи (1987).
Меньше - лучше. Если вы хотите минимизировать число появлений некоторых дефектов продукта, вычислите следующее отношение С/Ш:
Eta = -10 * log10 [(1/n) * ![]() (yi2)] for
i = 1 to no. vars see outer arrays
(yi2)] for
i = 1 to no. vars see outer arrays
Номинальное – наилучшее значение. Здесь вы имеете фиксированную величину сигнала (номинальное значение), и дисперсия вокруг этого значения рассматривается как результат действия шумов:
Eta = 10 * log10 (Mean2/Variance)
Такое отношение сигнал/шум может использоваться, когда идеальное качество совпадает с конкретным номинальным значением. Например, диаметр поршневых колец в двигателе автомобиля должен быть как можно ближе к стандартному, чтобы обеспечить высокое качество двигателя.Больше - лучше. Примерами такого типа инженерных задач является экономия топлива автомобиля (литров бензина на километр), прочность цементного раствора, сопротивление защитных материалов и так далее. Здесь используется следующее отношение С/Ш:
Eta = -10 * log10 [(1/n) * ![]() (1/yi2)] for
i = 1 to no. vars see outer arrays
(1/yi2)] for
i = 1 to no. vars see outer arrays
Eta = -10 * log10(s2) for i = 1 to no. vars see outer arrays
где s2 обозначает дисперсию характеристики качества по измерениям (переменным).Доля дефектов. Это отношение С/Ш используется для минимизации отходов, минимизации доли пациентов, у которых развиваются побочные реакции на препарат, и так далее. Тагучи также ссылается на значения Эта как на значения Омеги. Заметим, что это отношение С/Ш эквивалентно известному преобразованию логит (смотрите главу Нелинейное оценивание):
Eta = -10 * log10[p/(1-p)]
где
p доля дефектных изделий
Упорядоченные категории (аккумуляционный анализ). В некоторых случаях измерения характеристики качества могут быть получены только в терминах категорий. Например, покупатели могут категоризировать товар как превосходный, хороший, средний или ниже среднего. В этом случае вы пытаетесь максимизировать количество продуктов, оцениваемых как превосходные и хорошие. Обычно результат аккумуляционного анализа представляется в виде гистограммы.
Ортогональные массивы
Третий аспект робастных планов Тагучи весьма схож с трациционными методами. Тагучи разработал систему табулированных планов, которые позволяют оценить несмещенным (ортогональным) образом максимальное число главных эффектов при помощи минимального числа опытов в эксперименте. Планы на латинских квадратах, 2**(k-p) планы (Планы Плакетта-Бермана, в частности), и Планы Бокса-Бенкена также предназначены для достижения этой цели. Многие стандартные ортогональные массивы, табулированные Тагучи, идентичны дробным факторным двухуровневым планам, планам Плакетта-Бермана, планам Бокса-Бенкена, латинским квадратам, греко-латинским квадратам и так далее.
Анализ планов
Большая часть робастных планов эквивалентна обычному дисперсионному анализу (ДА) для соответствующих отношений С/Ш, в котором игнорируются взаимодействия второго порядка и выше. Заметим, что при оценке дисперсий ошибок обычно объединяются вместе главные эффекты пренебрежимых размеров.
Анализ отношений С/Ш в стандартных планах. Следует заметить, что все обсуждавшиеся ранее планы (например, 2**(k-p) планы, 3**(k-p) планы, смешанные 2-х и 3-х уровневые планы, латинские квадраты, центральные композиционные планы) могут быть использованы для анализа отношений С/Ш, которые вы вычислили. На самом деле, многие дополнительные диаграммы или другие опции, имеющиеся для указанных планов (например, оценивание квадратичных компонент и так далее), могут оказаться очень полезными при анализе вариабельности (С/Ш отношений) в производственном процессе.
Диаграмма средних. Визуализация итогов эксперимента состоит в нанесении на график средних Эта (С/Ш отношений) по уровням факторов. По этой диаграмме легко могут быть установлены оптимальные значения (то есть наибольшие отношения С/Ш) каждого фактора.
Проверочные или тестовые эксперименты. Для целей предсказания вы можете вычислить ожидаемое отношение С/Ш, при фиксировании пользователем определенных комбинаций установок факторов (игнорируя факторы, отнесенные в член ошибок). Эти предсказанные отношения С/Ш могут быть затем использованы для проведения проверочного эксперимента, в котором инженер действительно настраивает машину соответственно и сравнивает результаты наблюдаемого отношения С/Ш с предсказанным из предыдущего эксперимента отношением С/Ш. Если случаются большие отклонения, нужно сделать вывод, что модель простых главных эффектов не подходит.
В таких случаях Тагучи рекомендует преобразование зависимой переменной для обеспечения аддитивности факторов, то есть попытаться “заставить” модель главных эффектов соответствовать (Taguchi, 1987). Phadke (1989, глава 6) также детально обсуждает методы обеспечения аддитивности факторов.
Аккумуляционный анализ
Для анализа упорядоченных категориальных данных дисперсионный анализ непригоден. Вместо него модуль Планирование эксперимента представит кумулятивный график числа наблюдений в каждой категории. Для каждого уровня фактора программа выведет накопленную (кумулятивную) долю числа дефектных изделий. Таким образом, эта диаграмма дает ценную информацию относительно распределения категориальных отсчетов при различных значениях факторов.
Выводы
Вначале вы должны определить факторы плана или управляющие факторы, которые могут быть установлены конструктором или инженером. Это факторы эксперимента, которые вы будете устанавливать на различные уровни. Затем вы примете решение об использовании соответствующего ортогонального массива для эксперимента. Далее вы должны решить, как измерять интересующую вас характеристику качества. Помните, что большинство отношений С/Ш требует, чтобы в каждом опыте эксперимента производились многократные измерения, в противном случае, например, изменчивость (разброс) вокруг номинального значения не может быть оценена. Наконец, вы проводите эксперимент и определяете факторы, наиболее сильно влияющие на выбранное отношение С/Ш, и соответственно регулируете вашу машину или производственный процесс.
| В начало |
Специальные вопросы возникают, когда анализируются смеси компонент, которые в сумме должны давать константу. Например, если вы хотите оптимизировать вкус фруктового пунша, состоящего из соков 5 фруктов, то сумма долей всех соков в каждой смеси должна быть равна 100%. Такая задача оптимизации смесей часто встречается в производстве пищи, очистке или производстве химикатов или лекарств. Разработан ряд планов, специально для анализа смесей (смотрите, например, Cornell, 1990a, 1990b; Cornell и Khuri, 1987; Deming и Morgan, 1993; Montgomery, 1991).
Треугольные координаты
Общим способом, с помощью которого могут быть представлены пропорции в смеси, являются треугольные диаграммы (диаграммы на треугольнике). Например, предположим, что у вас есть смесь, которая состоит из 3 компонент A, B, C. Любая смесь трех компонент может быть представлена точкой в системе координат на треугольнике, определяемой тремя переменными.
Например, возьмем следующие 6 смесей из 3-х компонент.
| A | B | C |
|---|---|---|
| 1 0 0 0.5 0.5 0 |
0 1 0 0.5 0 0.5 |
0 0 1 0 0.5 0.5 |
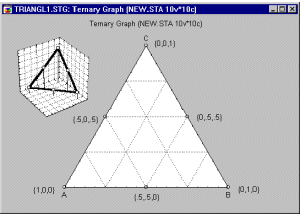
Чтобы определить координаты точки в треугольном графике, вы соединяете прямой линией точку с вершинами треугольника.
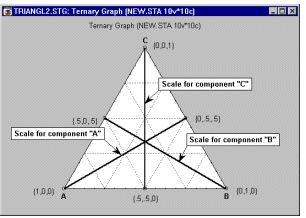
Вершина, соответствующая конкретному фактору представляет собой чистую смесь, то есть состоящую только из данной компоненты. Так что координата соответствующей вершине компоненты равна 1 (или 100% или любой другой величине в зависимости от шкалирования) и равна 0 (нулю) для всех других компонент. На стороне, противоположной соответствующей вершине, значение данной компоненты равно 0 (нулю), а для других компонент .5 (или 50% и так далее).
Тернарные поверхности и контуры
Можно теперь добавить четвертое измерение и нанести на график значения зависимой переменной или функцию (поверхность) для каждой точки внутри треугольника. Заметим, что поверхность отклика может быть представлена либо в 3-х мерном пространстве, где предсказываемый отклик (оценка Taste -Вкуса) наносится, как расстояние поверхности от плоскости треугольника, либо представлена в виде контурной диаграммы, где контуры равной высоты наносятся в 2-х мерном треугольнике.
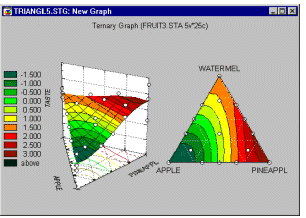
Канонический вид полиномов для смесей
Подгонка поверхности отклика к данным по смесям, в принципе, осуществляется таким же образом, как и подгонка поверхности для данных, полученных, например, с помощью центральных композиционных планов. Однако имеется проблема, состоящая в том, что в данных о смесях накладывается ограничение, состоящее в том, что сумма значений компонент должна быть постоянной.
Рассмотрим простой пример с двумя факторами A и B. Желательно подогнать простую линейную модель:
y = b0 + bA*xA + bB*xB
Здесь y обозначает зависимую переменную, bA и bB обозначают коэффициенты регрессии, xA и xB - значения факторов. Предположим, что xA и xB должны в сумме давать 1; тогда вы можете умножить b0 на 1=(xA + xB):y = (b0*xA + b0*xB) + bA*xA + bB*xB
или:
y = b'A*xA + b'B*xB
где b'A = b0 + bA и b'B = b0 + bB. Таким образом, оценивание в этой модели сводится к подгонке модели множественной регрессии без свободного члена. (Смотрите также Множественная регрессия для более детального рассмотрения вопросов, касающихся регрессии).Общие модели для смесей
Квадратичную и кубическую модели также можно упростить (как показано выше на примере простой линейной модели), что приводит к четырем стандартным моделям, обычно применяемым для подгонки смесей. Здесь приведены формулы для 3-х переменных для таких моделей (смотрите Cornell, 1990, для дополнительных подробностей).
Линейная модель:
y = b1*x1 + b2*x2 + b3*x3
Квадратичная модель:
y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3
Специальная кубическая модель:
y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3 + b123*x1*x2*x3
Полная кубическая модель:
y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3 + d12*x1*x2*(x1 - x2) + d13*x1*x3*(x1 - x3) + d23*x2*x3*(x2 - x3) + b123*x1*x2*x3
(Заметим, что коэффициенты dij также являются параметрами модели).Стандартные планы экспериментов для смесей
Обычно используются два типа стандартных планов экспериментов для смесей. Оба они оценивают поверхности отклика в вершинах треугольника и в центрах сторон. Иногда в эти планы добавляют дополнительные внутренние точки.
Симплекс-вершинные планы. При этом размещении точек плана m+1 для каждого фактора или компоненты в модели тестируются равноразмещенные точки:
xi = 0, 1/m, 2/m, ..., 1 i = 1,2,...,q
а также все их комбинации. Получающийся план называется simplex-lattice – симплекс-вершинным планом. Например, симплекс-вершинный план с {q=3, m=2} включает следующие смеси:| A | B | C |
|---|---|---|
| 1 0 0 .5 .5 0 |
0 1 0 .5 0 .5 |
0 0 1 0 .5 .5 |
| A | B | C |
|---|---|---|
| 1 0 0 1/3 1/3 0 2/3 2/3 0 1/3 |
0 1 0 2/3 0 1/3 1/3 0 2/3 1/3 |
0 0 1 0 2/3 2/3 0 1/3 1/3 1/3 |
| A | B | C |
|---|---|---|
| 1 0 0 1/2 1/2 0 1/3 |
0 1 0 1/2 0 1/2 1/3 |
0 0 1 0 1/2 1/2 1/3 |
| A | B | C |
|---|---|---|
| 2/3 1/6 1/6 |
1/6 2/3 1/6 |
1/6 1/6 2/3 |
Ограничения снизу
Для всех планов, описанных выше, требуются точки-вершины, то есть чистые смеси, состоящие из одной компоненты. На практике такие точки обычно неприемлемы, т.к. не могут производиться из-за соображений стоимости или других ограничений. Например, предположим, что вы хотели бы изучить эффект пищевых добавок на вкус фруктового пунша. Дополнительный ингредиент может варьироваться лишь в узких пределах, например, он не может превышать некоторого процента общей массы. Ясно, что фруктовый пунш, составленный только из чистой добавки, не будет на самом деле пуншем. Такого рода ограничения весьма типичны.
Рассмотрим пример с тремя компонентами, где на
компоненту A наложено ограничение xA![]() .3. Общая сумма для
3-х компонентной смеси должна быть равной 1. Это
ограничение может быть показано на треугольной
диаграмме в виде прямой с треугольными
координатами для xA=.3, то есть прямой,
параллельной стороне треугольника,
противоположной вершине A.
.3. Общая сумма для
3-х компонентной смеси должна быть равной 1. Это
ограничение может быть показано на треугольной
диаграмме в виде прямой с треугольными
координатами для xA=.3, то есть прямой,
параллельной стороне треугольника,
противоположной вершине A.
Теперь можно построить план, как и ранее, с тем лишь условием, что одна компонента смеси удовлетворяет ограничению. Позднее, при проведении анализа, можно просмотреть оценки параметров так называемых псевдокомпонент, рассматривающих ограниченный треугольник как полный.
Множественные ограничения. Многомерные ограничения снизу можно рассматривать аналогично одномерным. Программа сконструирует множество внутри полного треугольника и затем поместит точки плана в нее согласно выбранному плану.
Ограничения сверху и снизу
Если имеются ограничения снизу и сверху (что часто бывает в экспериментах на смесях), то стандартные симплекс-вершинные и симплекс-центроидные планы не могут быть построены, поскольку область, определяемая ограничениями, не является больше треугольником и центры (например, вершины) могут не принадлежать области определения. Существует общий алгоритм нахождения точек-вершин и центроидов для таких планов с ограничениями.
Заметим, что вы все еще можете проводить анализ таких планов, подгоняя стандартные модели.
Анализ экспериментов для смесей
Анализ экспериментов для смесей похож на множественную регрессию со свободным членом, равным нулю. Как объяснялось ранее, основное ограничение: сумма всех компонент должна быть постоянной – может быть реализовано в подгонке модели множественной регрессии, не включающей свободный член. Если вы не знакомы с понятием множественной регрессии, смотрите Множественная регрессия.
Специальные модели, рассматриваемые обычно, описаны ранее. Суммируя это описание, отметим, что к значениям зависимой переменной подгоняется поверхность отклика возрастающей сложности, начиная с линейной модели, затем продолжая квадратичной моделью, специальной кубической моделью и, наконец, завершая полной кубической моделью. Ниже приведена таблица, показывающая число членов или параметров в каждой модели для некоторого числа компонент (смотрите таблицу 4, Cornell, 1990):
| Model (Degree of Polynomial) | ||||
|---|---|---|---|---|
| No. of Comp. |
Linear |
Quadr. |
Special Cubic |
Full Cubic |
| 2 3 4 5 6 7 8 |
2 3 4 5 6 7 8 |
3 6 10 15 21 28 36 |
-- 7 14 25 41 63 92 |
-- 10 20 35 56 84 120 |
Дисперсионный анализ
Для того чтобы решить, какая модель из иерархии моделей возрастающей сложности дает достаточно хорошее согласие с наблюдаемыми данными, обычно их сравнивают пошагово. Например, рассмотрим смесь 3-х компонент, к которой подгоняется полная кубическая модель.| ANOVA; Var.:DV (mixt4.sta) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 Factor mixture design; Mixture
total=1., 14 Runs Sequential fit of models of increasing complexity |
||||||||||
| Model |
SS Effect |
df Effect |
MS Effect |
SS Error |
df Error |
MS Error |
F |
p |
R-sqr |
R-sqr Adj. |
| Linear Quadratic Special Cubic Cubic Total Adjusted |
44.755 30.558 .719 8.229 91.627 |
2 3 1 3 13 |
22.378 10.186 .719 2.743 7.048 |
46.872 16.314 15.596 7.367 |
11 8 7 4 |
4.2611 2.0393 2.2279 1.8417 |
5.2516 4.9949 .3225 1.4893 |
.0251 .0307 .5878 .3452 |
.4884 .8220 .8298 .9196 |
.3954 .7107 .6839 .7387 |
Чистая ошибка и потеря согласия. Полезность оценивания чистой ошибки для установления общей потери согласия было ранее обсуждено в разделе о центральных композиционных планах. Если некоторые опыты плана повторяются (реплицируются), то можно вычислить оценку дисперсии ошибки. Эта оценка дает хорошее представление о ненадежности измерений независимо от подгоняемой модели, поскольку основывается на одинаковых установках факторов (смесей в нашем случае). Можно тестировать остаточную изменчивость после подгонки текущей модели, используя эту оценку чистой ошибки. Если этот тест статистически значим, то есть остаточная изменчивость значительно больше вариабельности, обусловленной чистой ошибкой, тогда можно сделать вывод, что, вероятно, имеются дополнительные существенные различия между смесями, не описываемые текущей моделью. Таким образом, может иметь место общая потеря согласия текущей модели. В этом случае попытайтесь использовать более сложную модель, вероятно добавляя в нее отдельные члены из модели более высокого порядка (например, добавляя только член b13*x1*x3 в линейную модель).
Оценки параметров
Обычно после подгонки конкретной модели следует просмотреть оценки параметров. Заметим, что на линейные члены в моделях для смесей наложены ограничения (сумма компонент должны быть константой). Следовательно, независимые критерии значимости не могут быть выполнены.
Псевдокомпоненты
Чтобы избежать влияния разных шкал измерения компонет смеси обычно их перекодируют в так называемые псевдокомпоненты (смотрите также Cornell, 1993, глава 3):
x'i = (xi-Li)/(Total-L)
Здесь x'i обозначает i-ую псевдокомпоненту, xi обозначает исходные значения компоненты, Li – ограничение снизу (предел) для i-ой компоненты, L – сумма всех ограничений снизу для всех компонент плана, а Total есть суммы значений всех компонент смеси.Вопрос об ограничениях снизу также обсуждался в этом разделе. Если план является стандартным симплекс-вершинным или симплекс-центроидным, то это преобразование приводит просто к другой шкале измерения факторов (строится субтреугольник (субсимплекс), определяемый ограничениями снизу). Однако вы можете вычислять оценки параметров, основываясь на исходной (не преобразованной) метрике компонент, участвующих в эксперименте. Если вы используете подогнанные значения параметра для целей прогноза (то есть предсказываете значения зависимой переменной), то часто более удобно использовать параметры для непреобразованных компонент. Заметим, что диалоговый режим получения результатов в экспериментах для смесей содержит опции для прогноза зависимой переменной в задаваемых пользователем значениях компонент в исходной метрике.
Графические опции
Поверхности и контуры. Конкретная подогнанная модель может быть визуализирована в виде диаграммы поверхности на треугольнике или в виде контурной диаграммы, которая, по желанию, может также включать соответствующую подогнанную функцию.
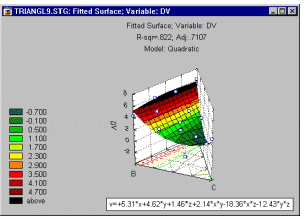
Заметим, что подогнанная функция, представленная в виде поверхности или контурной диаграммы, всегда соответствует оценкам параметров для псевдокомпонент.
Категоризованные поверхности. Если план содержит реплики, и они закодированы в вашем массиве данных, то вы можете использовать Категоризованные графики для просмотра соответствующих подгонок, реплика за репликой.
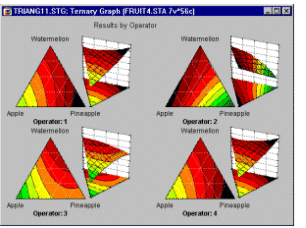
Конечно, если у вас есть другие категориальные переменные (например, оператор или экспериментатор, машина и так далее), вы можете также категоризовать 3-х мерную диаграмму поверхности и для таких переменных.
Графики следа отклика. Одним из методов оказания помощи при интерпретации поверхности отклика на треугольнике является график следа ожидаемого отклика. Предположим, что вы смотрите на контурную диаграмму поверхности отклика для трех компонент. Тогда определим базисную смесь двух компонент, например, установив A и B на уровне 1/3. Удерживая относительные пропорции A и B постоянными (то есть равными установленным значениям), вы можете нанести на диаграмму оценку отклика (значения зависимой переменной) для различных значений C.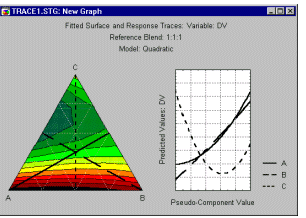
Если базисная смесь для A и B составляет 1:1, то линия следа является осью фактора C; то есть прямой между вершиной C и серединой противоположной стороны треугольника. Графики следа для других смесей также могут быть получены. Обычно на графике видны следы всех компонент для конкретной базисной смеси.
Графики остатков. Наконец, весьма важно после принятия решения о выборе модели, просмотреть остатки, чтобы найти выбросы и определить области плохой и хорошей подгонки. Кроме того, следует просмотреть стандартный нормальный график остатков и диаграмму рассеяния наблюдаемых значений против предсказываемых. Помните, что множественная регрессия (подгонка поверхности) предполагает, что остатки распределены нормально, и следует тщательно просмотреть остатки на наличие выбросов).
| В начало |
Обзор
Как уже говорилось при обсуждении планов для смесей, на интересующие нас экспериментальные области могут быть наложены ограничения. Пипель и Сни (Piepel, 1988) и Snee, 1985) предложили алгоритм для нахождения вершин и центроидов в областях с ограничениями.
Планы для экспериментальных областей с ограничениями
Когда в эксперименте со многими факторами имеются ограничения на значения факторов и их комбинаций, не ясно, как подойти к решению такой задачи. Разумный подход состоит в включении в эксперимент экстремальных вершинных точек и центроидов ограниченной области, которые обычно образуют хорошее ее покрытие (например, смотрите Piepel, 1988; Snee, 1975). В самом деле, планы для смесей, рассмотренные в предыдущем разделе, дают примеры таких планов, поскольку они обычно строятся так, чтобы включать в эксперимент вершины и центры ограниченной области, содержащейся в треугольнике (симплексе).
Линейные ограничения
Обычный способ задания большинства ограничений состоит в применении линейных неравенств (смотрите Piepel, 1988):
A1x1 + A2x2 + ... + Aqxq
+ A0 ![]() 0
0
Проблема нескольких ограничений сверху и снизу на значения компонент смеси была обсуждена ранее в связи с экспериментами для смесей. Например, предположим, что в 3-х компонентной смеси фруктовых соков ограничения сверху и снизу на компоненты таковы (смотрите пример 3.2 в работе Cornell 1993):
40% ![]() Watermelon (x1)
Watermelon (x1) ![]() 80%
80%
10% ![]() Pineapple
(x2)
Pineapple
(x2) ![]() 50%
50%
10% ![]() Orange (x3)
Orange (x3)
![]() 30%
30%
| Watermelon: |
x1-40 -x1+80 |
| Pineapple: |
x2-10 -x2+50 |
| Orange: |
x3-10 -x3+30 |
Таким образом, проблема нахождения точек плана для экспериментов на смесях с компонентами, на которые наложено несколько ограничений сверху и снизу, является частным случаем общих линейных ограничений.
Алгоритм Пипеля и Сни
Для специального случая смесей с ограничениями часто используются алгоритмы типа XVERT (см., например, Cornell, 1990) для того чтобы найти вершинные и центроидные точки для ограниченных областей (внутри треугольника, тетраэдра). Пипелем и Сни (Piepel, 1988 и Snee, 1979) был предложен общий алгоритм для нахождения вершин и центров тяжести (центроидов) и приложимый как к смесям, так и к не-смесям. Общий подход подробно описан Сни (Snee, 1979).
А именно, программа рассматривает ограничения, записанные с помощью линейных неравенств, как это было описано выше, одно за другим. Каждое ограничение описывает прямую (или гиперплоскость), проходящую в экспериментальной области. Для каждого последовательного ограничения программа оценивает, пересекает ли она текущую ограниченную область. Если это так, вычисляются новые вершины, определяющие новую экспериментальную область, подправленную с учетом последнего ограничения. Затем проверяется, не становятся ли предыдущие ограничения излишними, то есть определяют прямую или плоскость, целиком находящуюся вне рассматриваемой области. После того как обработаны все ограничения, программа вычисляет центроиды для сторон ограниченной области (упорядоченные по запросу пользователя). В двумерном (двухфакторном) случае можно легко воссоздать этот процесс, просто проводя прямые через экспериментальную область (по одной на ограничение), так что получится искомая область.
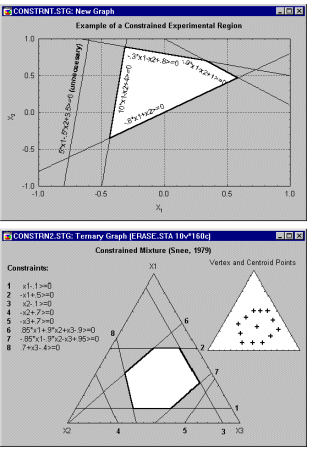
Для более подробной информации, см. оригинальные работы Piepel (1988) или Snee (1979).
Выбор точек эксперимента
Как только вершины и центры вычислены, вы сталкиваетесь с проблемой выбора подмножества точек для эксперимента. Если каждый его опыт дорогостоящ, то не разумно использовать все вершины и центроиды. В частности, если имеется много факторов и ограничений, то число центроидов может расти очень быстро.
Если вы просеиваете большое число факторов и не интересуетесь нелинейными эффектами, то, выбирая только вершины, как правило, получаете хорошее покрытие экспериментальной области. Чтобы увеличить статистическую мощность (увеличить число степеней свободы для члена ошибок дисперсионного анализа), можно включить несколько опытов с факторами, установленными в центроиде всей ограниченной области.
Если вы рассматриваете несколько моделей, которые могут подходить к данным, можно использовать опции D- и A-оптимальных планов, описанных в следующем разделе. Эти опции помогут отобрать точки плана, извлекая максимум информации из ограниченной экспериментальной области для ваших моделей.
Анализ планов для поверхностей и смесей с ограничениями
Как уже отмечалось в разделах о центральных композиционных планах и планах для смесей, если точки в ограниченной области выбраны для окончательного эксперимента, и интересующие нас значения зависимых переменных получены, анализ проводится стандартным образом.
Например, Cornell (1990, стр. 68) описывает эксперимент с тремя пластификаторами и их воздействие на толщину винилового покрытия автомобильных сидений. Производственные ограничения на три компоненты пластификатора x1, x2 и x3 следующие:
.409 ![]() x1
x1 ![]() .849
.849
.000 ![]() x2
x2
![]() .252
.252
.151 ![]() x3
x3
![]() .274
.274
| x1 | x2 | x3 |
|---|---|---|
| .8490 .7260 .4740 .5970 .6615 .7875 .6000 .5355 .7230 |
.0000 .0000 .2520 .2520 .1260 .0000 .1260 .2520 .1260 |
.1510 .2740 .2740 .1510 .2125 .2125 .2740 .2125 .1510 |
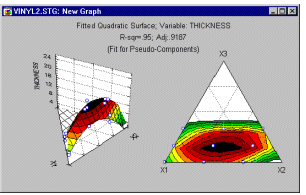
| В начало |
Обзор
В разделе стандартных факторных планов (смотрите Дробные 2**(k-p) факторные планы и 3**(k-p) планы, планы Бокса-Бенкена, и Смешанные 2-х и 3-х уровневые планы) и центральных композиционных планов обсуждалось свойство ортогональности. Коротко говоря, если уровни установок факторов не коррелированы, то есть изменяются независимо друг от друга, то говорят, что они ортогональны. (Если вы знакомы с матричной и векторной алгеброй, два вектор-столбца X1 и X2 в матрице ортогональны, если X1'*X2= 0). Интуитивно понятно, что можно извлечь максимальное количество информации о зависимой переменной в экспериментальной области (область, определяемая мыслимыми уровнями установок факторов), если все эффекты факторов ортогональны друг другу. Обратно, предположим, что проводится эксперимент из четырех опытов для двух факторов следующим образом:
| x1 | x2 | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 |
1 1 -1 -1 |
1 1 -1 -1 |
Процедуры D- и A-оптимальных планов предоставляют различные опции для отбора из списка подходящих точек-кандидатов (то есть комбинаций установок факторов) тех точек, которые извлекают из экспериментальной области максимальное количество информации для модели, которую вы хотите подогнать к данным. Вы уже имеете список точек-кандидатов, например, вершин и центроидов, вычисленных с помощью Планов для поверхностей и смесей с ограничениями, тип ожидаемой модели, число опытов. Тогда будет построен план с заданным числом опытов, который обеспечит максимальную ортогональность столбцов матрицы плана.
Смысл D- и A-оптимальности обсуждается, например, в монографии Бокса и Дрейпера (Box и Draper, 1987, глава 14). Различные алгоритмы, используемые для поиска оптимальных планов, обсуждаются в работах Dykstra (1971), Galil и Kiefer (1980) и Mitchell (1974a, 1974b). Подробное сравнительное описание алгоритмов проводится в работе Cook и Nachtsheim (1980).
Основные идеи
Техническое обсуждение идей, лежащих в основе D- и A-оптимальных планов, а также их ограничения находятся за пределами этого обсуждения. Однако, основные идеи достаточно прозрачны. Рассмотрим снова простой двухфакторный эксперимент из четырех опытов:
| x1 | x2 | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 |
1 1 -1 -1 |
1 1 -1 -1 |
| x1 | x2 | |
|---|---|---|
| x1 x2 |
1.0 1.0 |
1.0 1.0 |
| x1 | x2 | |
|---|---|---|
| Run 1 Run 2 Run 3 Run 4 |
1 1 -1 -1 |
1 -1 1 -1 |
| x1 | x2 | |
|---|---|---|
| x1 x2 |
1.0 0.0 |
0.0 1.0 |
Определитель матрицы плана. Определитель D квадратной матрицы (подобной корреляционной матрице 2 на 2, показанной выше) является числом, количественно выражающим независимость столбцов или строк матрицы или степень сводимости их друг к другу. Для случая 2 на 2 он просто равен произведению диагональных элементов минус произведение внедиагональных элементов (для матриц большей размерности вычисления более сложные). Например, для двух матриц, показанных выше, определитель D равен, соответственно:
| D1 = |
|1.0 1.0| |1.0 1.0| |
= 1*1 - 1*1 = 0 |
| D2 = |
|1.0 0.0| |0.0 1.0| |
= 1*1 - 0*0 = 1 |
D-оптимальные планы. Это базовое соотношение обобщается для матриц плана больших размерностей. Чем более зависимы векторы-столбцы матрица плана, тем более близок к 0 (нулю) детерминант корреляционной матрицы для этих векторов, а чем более независимы столбцы, тем больше детерминант этой матрицы. Таким образом, нахождение матрицы плана с максимальным детерминантом D означает нахождение плана, в котором эффекты факторов максимально независимы друг от друга. Этот критерий называется критерием D-оптимальности.
Матричные обозначения. В действительности обычно проводятся вычисления с ковариационной (а не корреляционной) матрицей. В матричных обозначениях, если матрица плана обозначается X, то интересующая нас величина есть детерминант матрицы X’X (X-транспонированнная, умноженная на X). Таким образом, поиск D- optimal - D-оптимальных планов заключается в максимизации |X’X|, где (|..|) обозначают детерминант матрицы.
A-оптимальные планы. Другим способом взглянуть на проблему независимости является максимизация суммы диагональных элементов матрицы X’X при минимизации внедиагональных элементов. Так называемый критерий следа или критерий A-оптимальности воплощает эту идею. A-критерий определяется как:
A = trace(X'X)-1
где trace обозначает сумму диагональных элементов матрицы (X'X)-1.Информационная функция. Здесь следует упомянуть, что D-оптимальные планы минимизируют ожидаемую ошибку предсказания зависимой переменной, то есть такие плана будут максимизировать точность прогноза, а значит, информацию (которая определяется как обратная величина ошибки), извлекаемую из интересующей нас экспериментальной области.
Измерение эффективности плана
Было предложено несколько стандартных мер, суммарно оценивающих эффективность плана.
D-эффективность. Эта мера связана с критерием D-оптимальности:
D-efficiency = 100 * (|X'X|1/p/N)
Здесь p обозначает число факторов-эффектов плана (столбцов в X), а N – число требуемых опытов. Эта мера может быть интерпретирована как относительное число опытов (в процентах), которое требовалось бы ортогональному плану для достижения той же величины детерминанта |X'X|. Однако ортогональный план часто нереален. Во многих случаях, это лишь теоретический критерий. Следовательно, вы должны использовать эту меру лишь как относительный индикатор эффективности для сравнения с другими планами того же объема, построенными из того же списка точек-кандидатов плана. Также заметим, что эта мера - единственно осмысленная (и только она может сообщаться), если вы решили, что факторы (то есть установки факторов точек из списка точек-кандидатов) имеют минимум -1 и максимум - +1.A-эффективность. Эта мера относится к критерию A-оптимальности:
A-efficiency = 100 * p/trace(N*(X'X)-1)
Здесь p обозначает число факторов-эффектов плана (столбцов в X), N – число требуемых опытов, а trace означает сумму диагональных элементов матрицы (N*(X'X)-1)) (след матрицы). Эта мера может интерпретироваться, как относительное число опытов (в процентах), которое потребовалось бы ортогональному плану для достижения той же самой величины следа (X'X)-1. Однако, снова отметим, что вы должны использовать эту меру как относительный индикатор эффективности для сравнения других планов того же объема, построенных из того же списка точек-кандидатов. Более того, это единственно осмысленная мера, если вы решили перекодировать установки факторов от -1 до +1.G-эффективность. Эта мера вычисляется как:
G-efficiency = 100 * square root(p/N)/![]() M
M
Построение оптимальных планов
Средства построения оптимальных планов в модуле Планирование эксперимента будут “осуществлять поиск” оптимальные планы при заданном списке “точек-кандидатов”. Иными словами, при заданном списке точек, определяющих допустимую область, и определенном пользователем числе опытов окончательного эксперимента, программа будет отбирать точки для оптимизации соответствующего критерия. Этот “поиск” наилучшего плана не точный метод, а алгоритмическая процедура, использующая некоторые стратегии поиска для нахождения наилучшего плана (согласно некоторому критерию оптимальности).
Предложенные процедуры и алгоритмы поиска описаны ниже (для обзора и подробного сравнения, смотрите работу Cook и Nachtsheim, 1980). Они расположены в порядке скорости реализации: Последовательный метод или метод Дейкстры является наиболее быстрым, но часто приводит к неправильному результату, то есть к плану, не являющемуся оптимальным (например, строится только локально оптимальный плану, вопрос о котором будет коротко обсужден далее).
Последовательный метод или метод Дейкстры. Этот алгоритм принадлежит Дейкстре (Dykstra, 1971). Начиная с пустого плана, программа ведет поиск по списку точек-кандидатов и на каждом шаге отбирает одну, которая максимизирует выбранный критерий. Не проводятся итерации, программа просто последовательно отбирает заданное число точек. Таким образом, этот метод самый быстрый из обсуждаемых. Кроме того, по умолчанию, этот метод используется остальными для построения начального плана.Метод простого обмена (Винна-Митчелла). Этот алгоритм обычно приписывают работам Mitchell и Miller (1970) и Wynn (1972). Метод стартует с начального плана требуемого объема (по умолчанию строящийся с помощью алгоритма последовательного поиска, описанного выше). В каждой итерации одна точка (опыт) выбрасывается из плана, а одна – добавляется из списка кандидатов. Выбор точек для выбрасывания и добавления последовательный, то есть на каждом шаге точка, добавляющая меньше всего относительно выбранного критерия оптимальности выбрасывается из плана, затем алгоритм отбирает точку из списка кандидатов для максимального увеличения соответствующего критерия. Алгоритм останавливается, когда нет дальнейшего улучшения с помощью дополнительных изменений.
Алгоритм DETMAX (обмен с отклонениями). Этот алгоритм принадлежащий Митчеллу (Mitchell, 1974b), вероятно наилучший из известных и наиболее широко используемый для поиска оптимального плана. Подобно алгоритму простого обмена (Винна-Митчелла) вначале строится исходный план (по умолчанию с помощью алгоритма последовательного поиска, описанного выше). Поиск начинается с применения алгоритма простого обмена (Винна-Митчелла), как описано выше. Однако, если соответствующий критерий (D или A) не улучшается, алгоритм предпринимает отклонения. А именно, алгоритм добавляет или выбрасывает более одной точки за один раз, так что во время поиска число точек в плане может изменяться между ND+ Nотклонение и ND+ Nотклонение, где ND – требуемый объем плана, а Nотклонение обозначает максимально допустимое отклонение, определяемое пользователем. Итерации останавливаются, когда выбранный критерий (D или A) больше не улучшается с помощью максимального отклонения. Модифицированный алгоритм Федорова (одновременного переключения). Этот алгоритм представляет модификацию (Cook и Nachtsheim, 1980) основного алгоритма Федорова, описанного ниже. Он также начинается с исходного плана требуемого объема (по умолчанию строящегося с помощью алгоритма последовательного поиска). На каждой итерации алгоритм обменивается каждой точкой плана с отобранной из списка точек-кандидатов, чтобы оптимизировать план согласно выбранному критерию (D или A). В отличие от алгоритма простого обмена (Винна-Митчелла) алгоритм, описанного выше, в данном алгоритме обмен не последовательный, а одновременный. Так, на каждой итерации каждая точка плана сравнивается с каждой точкой из списка кандидатов, и обмен происходит парой, оптимизирующей план. Алгоритм останавливается, когда нет дальнейшего улучшения соответствующего критерия оптимальности.Алгоритм Федорова (одновременного переключения). Этот оригинальный метод одновременного переключения предложен В.В.Федоровым (см. Cook и Nachtsheim, 1980). Отличие данной процедуры от процедуры, описанной выше (модифицированный алгоритм Федорова), заключается в том, что на каждой итерации осуществляется только единственный обмен, то есть на каждой итерации оцениваются все возможные пары точек плана и списка кандидатов. Алгоритм обменивается парой, оптимизирующей план относительно выбранного критерия. Таким образом, этот алгоритм потенциально может быть весьма медленным, поскольку на каждой итерации осуществляется ND*NC сравнений для обмена единственной точкой.
Общие рекомендации
Если вы подумаете над основными стратегиями поиска, представленных различными алгоритмами, описанными выше, станет ясно, что не существует точного решения проблемы оптимального плана. Именно, детерминант матрицы X’X (и след ее обратной) являются сложными функциями списка точек-кандидатов. В частности, имеется несколько “локальных минимумов” относительно выбранного критерия оптимальности, например, в любой момент поиска план может казаться оптимальным, до тех пор, пока вы одновременно не выбросите половину точек плана и не выберете некоторые другие точки из списка кандидатов, но если вы обмениваетесь отдельными точками или только несколькими точками (как в алгоритме DETMAX), тогда улучшения не случится.
Следовательно, важно попробовать ряд начальных планов и несколько алгоритмов. Если после повторения оптимизации несколько раз со случайного старта получится тот же самый или близкий оптимальный план, тогда вы можете быть в достаточной мере уверены, что вы не “попали” в локальный минимум или максимум.
Кроме того, методы, описанные выше, сильно различаются способностью “попадания” в локальные минимумы или максимумы. Общее правило состоит в том, что чем медленнее алгоритм (то есть чем он ниже в списке, описанном выше), тем более вероятно, что он приведет к истинно оптимальному плану. Однако, заметим, что модифицированный алгоритм Федорова практически работает так же хорошо, как и не модифицированный алгоритм (смотрите Cook и Nachtsheim, 1980); следовательно, если не рассматривать фактор времени, мы рекомендуем модифицированный алгоритм Федорова как наилучший для практического использования.
D-оптимальность и A-оптимальность. По вычислительным соображениям (смотрите Galil и Kiefer, 1980), обновление следа матрицы (для критерия A-оптимальности) много медленнее, чем обновление детерминанта (для D-оптимальности). Так что, если вы выбираете критерий A-оптимальности, вычисления могут занимать значительно больше времени по сравнению с критерием D-оптимальности. Поскольку на практике имеется много других факторов, влияющих на качество эксперимента, (например, надежность измерения зависимой переменной), мы, вообще говоря, рекомендуем использование критерия D-оптимальности. Однако, в трудных ситуациях построения плана, например, когда выясняется, что имеется много локальных максимумов критерия D, и повторные попытки приводят к сильно различающимся результатам, вы можете попробовать несколько прогонов оптимизации критерия A , чтобы лучше изучить различные типы возможных планов.
Устранение вырожденности матрицы
Может оказаться, что в процессе поиска, программа не сможет вычислить обратную матрицу к X’X матрица (для A-оптимальности) или, что детерминант матрицы становится близок к 0 (нулю). В этом случае поиск обычно не может продолжаться. Чтобы избежать подобной ситуации, программа осуществляет оптимизацию, основываясь на подправленной матрице X’X :
X'Xaugmented = X'X + ![]() *(X0'X0/N0)
*(X0'X0/N0)
“Подправление” планов
Свойства оптимальных планов могут быть использованы для “подправления” планов. Например, предположим, что вы используете ортогональный план, но некоторые данные потеряны (например, из-за неисправности оборудования), и вследствие этого некоторые интересующие вас эффекты не могут быть оценены. Вы, конечно, можете переделать потерянные опыты, но, предположим, что у вас нет ресурсов для того, чтобы переделать их все. В этом случае вы можете построить список точек-кандидатов из всех подходящих для этого точек экспериментальной области, добавить к этому списку все точки, для которых вы уже проделали опыты, и проинструктировать программу всегда включать эти точки в окончательный план (и никогда их не исключать, то есть вы можете пометить их в списке кандидатов с помощью опции непременного (насильственного) включения). Теперь можно исключать из плана лишь те точки, в которых вы пока не ставили опытов. Подобным образом вы можете, например, найти единственный опыт, добавив который к эксперименту, вы оптимизируете соответствующий критерий.
Ограниченные экспериментальные области и оптимальный план
Типичным применением оптимального плана являются ситуации, когда интересующая нас экспериментальная область ограничена. Как описано ранее в этом разделе, существуют средства и возможности для нахождения вершин и центроидов в случае областей с линейными ограничениями и для смесей. Такие точки могут затем быть представлены в списке точек-кандидатов для построения оптимального плана заданного объема для конкретной модели. Таким образом, эти два свойства, будучи объединены, предоставляют очень мощное средство справиться с трудными ситуациями построения плана, когда интересующая нас область подвергнута сложным ограничениям, а мы желаем подогнать конкретную модель при наименьшем числе опытов.
| В начало |
Последующие разделы описывают некоторые методы анализа: Профили отклика/функции желательности, проведение Анализа остатков и выполнение Преобразования Бокса-Кокса зависимых переменных.
Смотрите также Дисперсионный анализ, Методы дисперсионного анализа и Компоненты дисперсии и смешанные модели ANOVA/ANCOVA.
Создание профиля предсказанного и желательного отклика
Основная идея. Типовая задача, часто решаемая на производстве, заключается в поиске набора условий или уровней входных переменных, которые позволяют получить продукт с наилучшими характеристиками, т.е. с наилучшими значениями переменных отклика. Процедуры, используемые для решения этой задачи обычно включают два шага: (1) предсказание отклика, т.е значений зависимых Y-переменных, с помощью подгонки моделирующего уравнения на основе имеющихся данных об отклике на заданных уровнях независимых X-переменных, (2) поиск уровней X-переменных, которые одновременно дают наиболее желательные предсказанные отклики Y-переменных. Derringer и Suich (1980) предложили в качестве примера этих процедур задачу нахождения состава ткани, наиболее устойчивого к истиранию. В ней даны такие переменные Y, как PICO показатель истирания, 200-процентный модуль, продолжительность воздействия и плотность. Характеристики продукта в терминах переменных отклика зависят от состава, переменных X, таких как hydrated silica level – доля гидрата кварца, silane coupling agent level – доля соединения силана и sulfur. Задача состоит в нахождении уровней переменных X, которые максимизируют желательность откликов Y. Решение должно учитывать тот факт, что уровни переменных X, которые максимизируют один отклик, могут не максимизировать другой отклик.
Профиль отклика/функции желательности в анализе таких планов, как 2**(k-p) (двухуровневые факторные) планы, 2-х уровневые отсеивающие планы, Максимально несмешанные 2**(k-p) планы, Планы 3**(k-p) и планы Бокса-Бенкена, Смешанные 2-х и 3-х уровневые планы, Центральные композиционные планы и Планы для смесей позволяет вам просматривать поверхность отклика, получаемую при подгонке наблюдаемых откликов с использованием уравнения, основанного на уровнях независимых переменных.
Профили предсказания. Когда вы анализируете результаты любого из перечисленных выше планов, для подгонки наблюдаемых откликов каждой зависимой переменных (содержащих различные коэффициенты, но одинаковые члены) используются отдельные уравнения предсказания. Как только эти уравнения построены, предсказанные значения для зависимых переменных могут быть вычислены для любой комбинации уровней предикторов. Профиль предсказания для зависимой переменной состоит из серии графиков, по одному на каждую независимую переменную (предиктор), предсказанных значений зависимой переменной при различных уровнях независимой переменной, при значениях других независимых переменных, равных константе на заданных уровнях, называемых текущими значениями. Если выбраны соответствующие текущие значения для независимых переменных, просмотр профиля предсказания поможет выяснить, какие уровни предикторов дают наиболее желательный отклик зависимой переменной. Исследователь может быть заинтересован в контроле предсказанных значений зависимых переменных только на текущих уровнях, которые принимают независимые переменные в течение эксперимента. В качестве альтернативы, исследователь может быть заинтересован в контроле предсказанных значений зависимых переменных на уровнях, отличных от текущих уровней независимых переменных, используемых в течение эксперимента, в целях выявления промежуточных уровней независимых переменных, которые могут дать даже более желательные отклики. Также, возвращаясь к примеру Derringer и Suich (1980), для некоторых переменных отклика наиболее желательные значения не обязательно являются наиболее экстремальными значениями, например, наиболее желательное значение продолжительности воздействия может лежать в узком диапазоне возможных значений. Желательность отклика. Разные зависимые переменные могут по-разному зависеть от различных взаимосвязей между вкладами переменной и желательностью вкладов. Более светлое пиво может быть более желательным, но более вкусное пиво также может быть более желательным: оба свойства - большей "светлости" и большей "вкусности" - более желательны. Взаимосвязь между предсказанными откликами зависимой переменной и желательностью откликов называется функцией желательности. Derringer и Suich (1980) выработали процедуру для определения взаимосвязи между предсказанными откликами зависимой переменной и желательностью откликов, процедуру, которая предполагает до трех точек "перегиба" функции. Применительно к примеру по составу ткани, описанного выше, эти процедуры включают преобразование вкладов каждой из четырех результирующих переменных, характеризующих состав ткани, в желательности вкладов, которые находятся в интервале от 0.0 для нежелательных до 1.0 для очень желательных. Например, их функция желательности для hardness - плотности состава ткани определяется заданием значения желательности 0.0 для показателя hardness, меньшего 60 или большего 75, значения желательности 1.0 для срединного показателя hardness 67.5, значения желательности, увеличивающегося линейно от 0.0 до 1.0 для показателей hardness между 60 и 67.5 и значения желательности, уменьшающегося линейно от 1.0 до 0.0 для показателей hardness между 67.5 и 75.0. В более общем смысле это означает, что процедуры нахождения функций желательности должны обеспечивать кривизну "уменьшения" желательности между точками перегиба функции. После преобразования предсказанных значений зависимых переменных при различных комбинациях уровней предикторных переменных в индивидуальные показатели желательности может быть вычислена общая желательность исходов при различных комбинациях уровней предикторных переменных. Derringer и Suich (1980) предложили вычислять общую желательность как геометрическое среднее отдельных желательностей (что имеет интуитивно понятный смысл, так как, если отдельная желательность некоторого исхода равна 0.0, или нежелательна, общая желательность тоже будет равна 0.0, или нежелательна, не учитывая при этом, насколько желательны другие отдельные исходы — геометрическое среднее берет произведение всех значений и возводит это произведение в степень, обратную числу значений). Процедура Derringer и Suich дает простой способ преобразования предсказанных значений для множественных зависимых переменных в простой показатель общей желательности. Проблема одновременной оптимизации нескольких переменных отклика затем сводится к выбору уровней предикторных переменных, которые максимизируют общую желательность откликов зависимых переменных. Выводы. Когда исследователь разрабатывает продукт, для которого известно, что его свойства зависят от его "ингредиентов", создание лучшего продукта, возможно, требует определения эффектов его ингредиентов на каждое свойство продукта в отдельности и последующее нахождение гармонического сочетания ингредиентов, оптимизирующего общую желательность продукта. В терминах анализа данных, процедура, которая производит максимизацию желательности продукта, делает следующее: (1) находит адекватные модели (т.е. уравнения предсказания) для предсказания свойств продукта как функцию уровней независимых переменных, и (2) определяет оптимальные уровни независимых переменных для получения высокого общего качества продукта. Эти два шага, если им точно следовать, с большой вероятностью приводят к большему успеху в усовершенствовании продукта, чем придуманная, но статистически сомнительная методика надежды на случайные достижения и открытия, которые радикально улучшили бы качество продукта.Анализ остатков
Основная идея. Расширенный анализ остатков - это ряд диагностических средств для контроля различных остаточных и предсказанных значений, проверки адекватности модели предсказания, необходимости преобразований переменных модели, и наличия выбросов в данных.
Остатки – это отклонения наблюдаемых значений зависимой переменной от предсказанных значений, получаемых текущей моделью. Модели ANOVA, используемые в анализе откликов зависимой переменной, делают некоторые предположения о виде распределения остатков (но не предсказанных значений) зависимой переменной. Эти предположения можно выразить, сказав, что модель ANOVA предполагает нормальность, линейность, постоянство дисперсии и независимость остатков. Эти свойства остатков для зависимой переменной могут быть проверены с помощью Статистик остатков.Преобразование Бокса-Кокса зависимых переменных
Основная идея. В дисперсионном анализе делается предположение, что дисперсии различных групп (состояний эксперимента) однородны, и что они не коррелированы со средними. Если распределение значений в каждом состоянии асимметрично, и если средние коррелированы со стандартными отклонениями, то исследователь часто может применить соответствующее степенное преобразование зависимой переменной для стабилизации дисперсий, а также для уменьшения или устранения корреляции между средними и стандартными отклонениями. Преобразование Бокса-Кокса используется для выбора соответствующего (степенного) преобразования зависимой переменной.
Опция Преобразование Бокса-Кокса выдает график Остаточной суммы квадратов, даваемой моделью, как функции значения лямбда, где лямбда используется для задания преобразования зависимой переменной,| y' = ( y**(lambda) - 1 ) / ( g**(lambda-1) * lambda) | if lambda |
| y' = g * natural log(y) | if lambda = 0 |
| Approximate lambda |
Suggested transorfmation of y |
|---|---|
| -1 -0.5 0 0.5 1 |
Reciprocal Reciprocal square root Natural logarithm Square root None |
| В начало |
![]()
© Copyright StatSoft, Inc., 1984-1998
STATISTICA is a trademark of StatSoft, Inc.