5.4. Координация нечетких решений в многоуровневой иерархической системе

Процедура соединения элементов в многоуровневой иерархической системе может быть сведена к некоторой рекуррентной процедуре. Рассмотрим построение этой рекуррентной процедуры, основываясь на работе [54]. Этот алгоритм относится к классу безытеративных алгоритмов.

При принятии оперативных решений в сложной иерархической системе (рис.5.4) основной целью является нахождение на каждом уровне вектора решений , которые обеспечивают максимум системного вектора целевых функций при координационном задании , полученном от (N+1)-го уровня управления. Причем процесс принятия решений осуществляется дискретно в моменты времени и в общем случае, шаг дискретизации по управлению возрастает от нижних уровней к верхним. Часть решений (в основном на нижних уровнях) носит характер управляющих воздействий, а большая часть лишь координирует работу подсистем разных уровней. Назначение нижестоящим подсистемам целевых функций также является средством координации, однако в данной задаче предполагается, что они уже выбраны.

Найденное решение , должно принадлежать подмножеству допустимых для системы режимов (технологических, надежностных, экономических и т.д.) , т.е. быть согласованным с возможностями технологии.

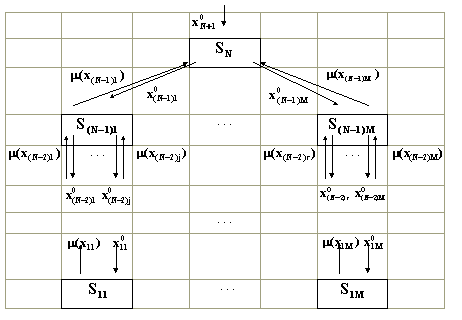
Рис.5.4. Структурная схема многоуровневой иерархической системы

Попытка непосредственного использования единого глобального критерия верхнего уровня с последующей его декомпозицией для подсистем всех уровней делает задачу оптимизации крайне сложной и игнорирует наличие собственных целевых функций у активных подсистем. К тому же, глобальная целевая функция не зависит явным образом от решений, принимаемых подсистемами нижестоящих уровней, что затрудняет выбор режимов работы подсистем и путей его улучшения [155]. Поэтому будем предполагать, что для каждой j-ой подсистемы i-го уровня заданы свои цели на множествах решений подсистем, а системная целевая функция является векторной и зависит как от глобального критерия , так и от целевых функций подсистем .

В настоящее время принято исследовать вопросы оптимизации для двухуровневой системы и принимать эту задачу как основной модуль для любой N-уровневой системы [155], причем для решения задачи на (i -1)-м уровне считается заданным результат оптимизации на уровне i. Или, если записать в виде

,

где - число подсистем на i-м уровне управления, то предполагается, что при нахождении решений , все решения , уже приняты. Поэтому для оптимизации в многоуровневых системах в основном используются различные итеративные методы [162].

Применим метод инвариантного погружения [53] и будем рассматривать вместо задачи с четким решением (планом) на (N+1) -м уровне и фиксированным числом уровней Nнекоторое семейство задач с N = 1,2,3, ... ; . В этом случае максимум функций будет зависеть от N и . Эту зависимость мы и постараемся найти. Таким образом, исходная четкая задача с помощью метода инвариантного погружения фактически размывается, что приводит к понятию нечеткого решения для каждого уровня управления. Это позволяет нам применить для решения задачи аппарат теории нечетких множеств.

На возможность преодоления трудностей, вызываемых наличием векторного критерия, отсутствием унимодальности, дискретностью и сложностью исходной задачи путем преднамеренного внесения неопределенности или случайности, в решении задачи указывалось еще в работе [194]. Но в отличие от предлагаемого подхода предлагается осуществлять не "размывание", а рандомизацию решения для одноуровневых систем.

В качестве характеристики принимаемых решений по отдельным подсистемам j и для всей системы в целом будем использовать функцию принадлежности принимаемых решений к подмножеству допустимых, эффективных и скоординированных решений , причем эта функция не сводится для четких решений к функции , так как она включает в себя не только характеристику эффективности решения, но и характеристику его допустимости (степень принадлежности решения к подмножеству допустимых режимов С) и скоординированности с целями и ограничениями нижестоящих подсистем (степень принадлежности решения к подмножеству скоординированных режимов К). Функции принадлежности определяются на множестве решений . Эффективность решений задается нечеткой целью как нечеткое подмножество с функцией принадлежности , допустимость решений - нечетким подмножеством с функцией принадлежности и скоординированность - нечетким множеством с функцией принадлежности . Результирующее влияние нечеткой цели G, нечеткого ограничения С и нечеткой координации К на выбор решения может быть представлено пересечением . Функция принадлежности для пересечения задается соотношением

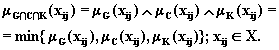(5.10)

Тогда нечеткое подмножество будем называть нечетким решением подсистемы jуровня i, причем

. (5.11)

При наличии материальных потоков между иерархическими уровнями или различных уравнений материального баланса, описывающих группы подсистем, решение для подсистемы r на уровне (i + 1) может быть связано с решением подсистем i-го уровня уравнением

(5.12)

В случае, когда множество решений Х состоит только из одного параметра, уравнение может быть записано в виде

. (5.13)

Решения могут быть более сложными и характеризоваться вектором параметров , например давлением газа , расходом и температурой газа . В общем случае решения могут приниматься и для нестационарных режимов работы системы, тогда вместо зависимостей (5.12) будут фигурировать дифференциальные уравнения в частных производных.

Системное скоординированное решение на уровне N может быть определено выражением вида

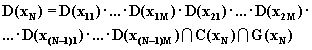(5.14)

Из записи системного решения (5.14) несложно получить простую рекуррентную процедуру для принятия решений в N - уровневой иерархической системе.

Вследствии инвариантности введенного описания по уровням системы из (5.14) следует, что

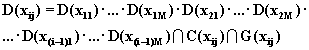(5.15)

в частности,

(5.16)

В связи с тем, что в иерархической структуре решение на i-м уровне управления зависит только от состояния на этом уровне и решений, принимаемых вышестоящим (i+1)-м и нижестоящим (i-1)-м уровнями управления (что обусловлено самим принципом принятия решений в иерархических системах), в решении учитываются все решения нижестоящих подсистем согласно выражению (5.195). Тогда (5.16) можно записать через нечеткие решения нижестоящего уровня следующим образом:

. (5.17)

Причем для принятия решения управляющая подсистема rуровня (i+1) должна предварительно свернуть решения нижестоящих подсистем в системное решение . Тогда (5.17) можно записать в виде

. (5.18)

Наличие такой рекуррентной процедуры обусловлено особенностью принятия решений в иерархической структуре и наличием самостоятельных прав по обработке информации и принятию решений в каждой системе управления. Однако в отличие от общепринятого представления решений в четкой форме (т.е. в виде конкретных числовых значений параметров управления) допустим, что решения всех подсистем в процессе координации решений является нечеткими и задаются для каждой подсистемы функциями принадлежности . Тогда для функций принадлежности рассматриваемого подмножества эффективных и допустимых решений уравнение (5.18) приобретает вид

, (5.19)

где (5.20)

Бинарная операция Aнад функциями принадлежности может быть в каждом конкретном случае или алгебраическим произведением, или операцией Заде [98], или алгебраическим сложением. Выбор операции обуславливается типом операции над множествами, физическим смыслом функций принадлежности и аксиоматикой нечетких множеств [98].

Функция принадлежности характеризует согласно (5.10) межуровневую координацию К, причем для принятия решения на (i+1)-м уровне необходимо спроектировать координирующее решение на ось с учетом уравнения (5.13). Тогда функцию можно будет представить в виде

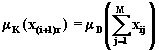(5.21)

Уравнение (5.21) наглядно показывает, что решение вышестоящего уровня может быть выполнено с помощью различных решений нижестоящих подсистем . Причем, анализируя выражение (5.20), можно сделать вывод, что при прочих равных условиях работа подсистемы r уровня (i+1) будет наиболее эффективной в случае, когда каждая подсистема jуровня i будет принимать оптимальные решения (максимизируя свою функцию принадлежности) и при определении решений подсистемам нижестоящего уровня мы будем стремиться максимизировать проекцию этих решений на ось , т.е.

. (5.22)

Это дает возможность характеризовать оптимальную стратегию подобно принципу оптимальности Р.Беллмана [98].

Оптимальное решение многоуровневой иерархической системы обладает тем свойством, что каковы бы ни были состояние и решение вышестоящего уровня управления в момент t, последующие решения нижестоящих уровней должны быть оптимальными относительно этого решения.

Применение принципа оптимальности позволяет реализовать наиболее эффективный способ координации решений, принимаемых на отдельных уровнях иерархии. Этот принцип позволяет до минимума сократить обмен информацией между уровнями и обеспечить локальную обработку информации по подсистемам.

Но только использование единого подхода к целевым функциям и ограничениям в теории нечетких множеств позволило получить адекватные характеристики нижестоящих подсистем, не сводящиеся только к экономическим аддитивным характеристикам в условиях полной определенности.

На основе этого принципа можно построить рекуррентную процедуру принятия решений, которая будет состоять из двух этапов для каждого (i+1)-го уровня управления.

1. Решается оптимизационная задача на декартовом произведении множеств с целевой функцией (5.22) для уровня (i+1) с учетом ограничения (5.13). Если подсистемы уровня i связаны между собой материальными потоками, то ограничение (5.13) необходимо дополнить системой ограничений - равенств и ограничений - неравенств:

, (5.23)

, (5.24)

описывающих связь подсистем на уровне i.

Результатом решения оптимизационной задачи является функция принадлежности .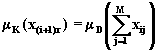

2. Находится нечеткое решение на ( i+1) - м уровне на основе формул (5.19) и (5.20).

Для принятия четкого решения на N-м уровне управления необходимо выбрать такое решение , для которого степень принадлежности к подмножеству эффективных и допустимых решений является максимальной, т.е.

. (5.25)

После принятия четкого решения на N-м уровне управления на основе решения оптимизационной задачи (5.22), (5.23), (5.24) при находятся четкие решения уровня (N-1) . Далее эта процедура повторяется до тех пор, пока не будут четко приняты все решения в системе .

Подсистемы управления первого уровня могут быть элементарными и не иметь координирующих функций, т.е.

. (5.26)

Активность подсистем первого уровня в этом случае проявляется в формировании своих нечетких решений

. (5.27)

Однако при наличии взаимосвязи подсистем первого уровня через технологический процесс возникает естественная необходимость координации решений подсистем, исходя из целевой функции и моделей, описывающих этот процесс. В этом случае координирующая функция будет получена на основе решения оптимизационных задач для сложных технологических процессов.

Целевые функции подсистем более высоких уровней могут быть специфическими для каждого уровня и состоять лишь в обеспечении эффективных режимов работы нижестоящих подсистем

. (5.28)

Если же вышестоящая подсистема имеет собственную цель G, то при принятии решений она будет учитывать цели и возможности нижестоящих подсистем через координирующее нечеткое решение в формуле (5.10). Эта функция принадлежности гарантирует назначение нижестоящим подсистемам режимов работы, близких к наиболее предпочтительным для них режимам, т.е. фактически отражает факт учета интересов подсистем в процессе принятия решений.

В общем случае функция принадлежности может быть условной, т.е. зависеть от некоторого параметра - . Например, если есть расход газа для подсистемы j уровня i, то - давление газа на ее выходе.

Описанная таким образом на языке теории нечетких множеств активная иерархическая система является полностью определенной, так как задана структура системы и выделены уровни иерархии, выявлены предпочтения для каждой подсистемы путем задания соответствующих функций принадлежности, система уравнений и ограничений, описывающих связи в иерархической системе.

Рекуррентная процедура предназначена для разрешения внутрисистемных конфликтов. Наличие двух этапов в рекуррентной процедуре связано с необходимостью разрешения в системе конфликтов двух видов: внутриуровневого, возникающего из-за несовместимости локальных целей отдельных элементов в рамках заданной структуры и ограничений, и межуровневого (между двумя смежным уровнями), имеющего место из-за того, что цель (задача) вышестоящего элемента не совпадает с обеспечением элементам нижестоящего уровня оптимальных режимов. Эти конфликты разрешаются последовательно с использованием первого и второго этапов рекуррентной процедуры. Особенности предлагаемого метода позволяют не только устанавливать наличие или отсутствие подобных конфликтов и их природу на основе использования соответствующих функций принадлежности в качестве характеристики многоуровневой системы, но и принимать эти функции принадлежности в качестве ориентиров для синтеза и целенаправленного изменения параметров и структуры системы. Необходимость учета всех этих факторов отмечена в работе [155].

Таким образом, в отличие от динамического программирования, данный метод направлен не на согласование решений, принимаемых для одной и той же системы в последовательные моменты, а для согласования решений по уровням в многоуровневой иерархической системе в определенный момент t, причем для каждого, в том числе и нижнего уровня (основного технологического процесса), может быть решена и динамическая задача.

Основная трудность решения задач оптимизации многоуровневых иерархических систем заключается в том, что решение нижестоящего уровня зависит от задания со стороны вышестоящего уровня (цели, ограничения), а решение вышестоящего уровня, в свою очередь, зависит от отклика элементов нижестоящего уровня. Эта дилемма разрешена путем введения на нижестоящем уровне понятия нечеткого оптимального решения.

Существует процесс координации, производимый до принятия решения нижестоящими элементами или после принятия решения (коррекция). Предлагаемый метод координации согласует решения в процессе принятия решений по оперативному управлению системой. Вышестоящий и нижестоящий элементы связаны между собой двумя видами сигналов. Сигнал, посылаемый наверх, несет вышестоящему элементу информацию о допустимости и эффективности режимов работы элементов (нечеткое оптимальное решение), а сигнал, идущий сверху вниз, конкретизирует задания, подлежащий выполнению на нижестоящем уровне. Вышестоящий элемент в связи с приоритетом действий должен выбрать для нижестоящих элементов стратегию поведения (выбор способа координации), изменения в структуре и параметрах нижестоящих элементов (аспект самоорганизации) и координирующее воздействие при фиксированной структуре и параметрах (аспект управления). Информация о нижестоящих элементах, необходимая вышестоящему элементу для принятия решения, зависит от цели решаемой задачи, от образа (модели) элементов и связей между ними.

Для многоуровневой иерархической системы важным является описание нижестоящего уровня как взаимодействие взаимосвязанных подсистем, каждая из которых преследует собственные цели. Поэтому основное внимание обращено на внутриуровневые и межуровневые взаимодействия. Предлагаемый подход полностью отвечает основным требованиям системного анализа, так как обеспечивает при моделировании целостность рассмотрения сложной иерархической системы за счет теории нечетких множеств, позволяющих целиком удерживать в поле зрения всю систему в целом для решения задачи на всех уровнях управления с позиции системной цели; всесторонность рассмотрения на основе учета основных элементов и процессов в системе и связей между ними; при существующем узком рассмотрении лишь отдельных процессов на определенных уровнях управления получается искаженное, одностороннее представление о системе, не позволяющее иметь достоверные оценки об отдельных подсистемах и судить о требованиях к ним для обеспечения их совместного целенаправленного функционирования в системе; достаточную степень упрощения при моделировании, которая позволяет адекватно отразить реальный процесс и учесть определяющие факторы в этой системе; это связано с тем, что при определении управляющих воздействий на систему рассматривается не сама система, а ее модель; слабое отражение разнообразия системы в модели ставит под сомнение правильность выбора тех или иных управляющих воздействий.

Применение системного подхода позволило сформулировать факторы, определяющие природу изменения эффективности и допустимости состояний сложной системы и свести массивы информации, описывающие состояние системы в различные моменты и при различных условиях, к небольшому числу обобщенных характеристик с целью наглядной интерпретации количественных данных о системе при подготовки их для принятия решения.

Функции принадлежности удовлетворяют основным требованиям, предъявленным к числовым характеристикам:

1. они представляют собой величины, зависящие от состояния элементов системы и связей между ними, и достаточно просто вычисляются исходя из имеющейся информации о системе (детерминистической, вероятностной, лингвистической);

2. каждая из функций принадлежности, построенных для элемента системы, дает наглядное представление об одном из свойств системы;

3. функция принадлежности допускает простую приближенную оценку на основе экспериментальных данных или экспертных оценок.

Одним из существенных достоинств решения многокритериальной задачи является тот факт, что в результате решения однокритериальной задачи мы получаем решение на границе какого-либо ограничения, т.е. она по сути дела представляет собой великолепный "генератор" узких мест, которые болезненно отражаются на поведении реального объекта и значительно снижают другие показатели режима работы – надежность, соответствие условиям рациональной разработки месторождения и т.д. Многокритериальная постановка задачи отличается большей близостью к реальной задаче и меньшей долей абстракции.

Использование языка теории нечетких множеств совместно с теорией иерархических многоуровневых систем в качестве метаязыка позволяет правильно отобразить основные свойства исходной системы и упростить процесс ее анализа. Принятая степень абстрагирования является наиболее приемлемой, так как более широкое обобщение будет бесплодным с точки зрения практики, а недостаточная степень абстрагирования приведет к невозможности решения задачи – она останется излишне сложной.

При использовании предлагаемого метода соблюдается гомоморфность каждой модели. В то же время формирование моделей происходит не за счет исключения отдельных параметров, а за счет объединения их в более крупные показатели по принципу, провозглашенному С. Биром: "Многое в одном".

На самом высоком иерархическом уровне рассматриваются вопросы распределения ресурсов и взаимовлияние между подсистемами с точки зрения всей системы в целом и вопрос об эффективности и допустимости ее режимов. Наиболее детально при анализе рассматриваются только те подсистемы, в которых имеется существенное снижение степени эффективности и допустимости режимов, а все, что не играет особой роли с системной точки зрения, исключается из дальнейшего детального рассмотрения. Таким образом, для введенной иерархической системы при переходе с низкого на более высокий уровень иерархии теряется некоторая информация о деталях, но появляется возможность судить о сравнительной важности различия аспектов исследуемого в задаче явления с точки зрения более высокого уровня.

Рассмотрение задач на каком-либо уровне управления позволяет дать ответ лишь на определенную группу вопросов, причем каждый из уровней имеет свои, только ему присущие ограниченные возможности.

Возможности обычного метода оптимизации после принятия решения по оперативному управлению иерархической системой исчерпываются. Предлагаемый же подход позволяет продолжать работу с той же моделью и принимать решения по дальнейшему совершенствованию системы, повышению эффективности ее работы на плановом режимах. Причем метод позволяет произвести многоцелевую оценку каждого управляющего воздействия, более просто и менее трудоемко получить оптимальное решение с использованием интерактивного режима.

При решении задачи, сформулированной в терминах нечетких множеств, нет необходимости точно задавать все границы принимаемых решений, что требует для точного задания каждой границы большой и трудоемкой работы. Функции принадлежности первоначально лишь грубо задают систему предпочтений и ограничений, допуская дальнейшее уточнение значений функции лишь в районе предполагаемой точки оптимума. Таким образом достигается сокращение непроизводительного труда специалистов по подготовке исходной информации для решения задачи и стимулируется их творческая инициатива для поисков новых неформальных возможностей улучшения решения при анализе информации, выданной ЭВМ.

Процесс координирования в системе осуществляется в связи с определенной целью или задачей так, чтобы вся система в целом достигала поставленной цели. Конфликт между нижестоящими подсистемами возникает из-за наличия у них собственных индивидуальных целей и из-за различных видов системных ограничений и связей. Действия координатора направлены на уменьшение такого внутрисистемного конфликта. Успех вышестоящей подсистемы в деятельности по координации можно оценивать с помощью введенной функции принадлежности режимов работы этой подсистемы к подмножеству эффективных и допустимых режимов.

Основная трудность решения задач оптимизации многоуровневых иерархических систем заключается в том, что решение нижестоящего уровня зависит от задания со стороны вышестоящего уровня (цели, ограничения), а решение вышестоящего уровня, в свою очередь, зависит от отклика элементов нижестоящего уровня. Эта дилемма разрешена путем введения на нижестоящем уровне понятия оптимального нечеткого решения.

Введем два понятия координируемости на языке теории нечетких множеств, которые соответствуют абстрактным определения работы [155] и имеют целью количественно рассчитать координируемость реальных систем.

Как мы уже определили ранее, управление с использованием функций принадлежности заключается в нахождении такого режима , для которого функция принадлежности принимает максимальное значение. Следовательно, задача имеет решение, если существует такой режим , для которого , т.е.

. (5.29)

Решения нижестоящих элементов j уровня i описываются функциями принадлежности , а решение задачи вышестоящих элементов r уровня (i+1) по координированию решений нижестоящих подсистем - функцией принадлежности . Отсюда следует, что задачи, решаемые нижестоящими элементами, координируемы между собой в момент tтогда и только тогда, когда справедливо следующее положение:

. (5.30)

Следовательно, координируемость задач между собой требует, чтобы эта задача имела решение хотя бы при одном и для этого решения множество частных задач D, решаемых нижестоящими элементами, также имело решение.

В случае, когда является максиминным или мультипликативным критерием, выражение (5.30) может быть записано виде

, (5.31)

т.е. в терминах теории нечетких множеств задачи, решаемые нижестоящими элементами, координируемы между собой в том случае, если нечеткое множество D не пусто

. (5.32)

Задачи, которые будут решаться нижестоящими элементами, координируемы относительно заданной глобальной цели G уровня (i+1) в момент t, если справедливо следующее предложение:

(5.33)

Так как является максиминным критерием, выражение (5.33) можно переписать в виде

. (5.34)

Исходя из этих двух понятий координируемости, постулат совместмости можно записать следующим образом.

Для успешной работы многоуровневой иерархической системы необходимо, чтобы цели (задачи) ее подсистем были скоординированы между собой и с глобальной целью всей системы в целом.

Система управления будет обладать свойством безусловной межуровневой согласованности, если управляющие воздействия со стороны вышестоящего уровня управления, максимизирующие согласно принципу оптимальности глобальную функцию принадлежности, одновременно максимизируют и локальные функции принадлежности нижестоящего уровня, т.е. это свойство будет присуще лишь идеально спроектированной системе.

Для реальной системы степень согласованности будет отличаться от 1, и потери при координации отдельных подсистем можно оценивать разностью между и при работе подсистемы j в общей системе.

5.5. Численные методы согласования нечетких решений

Построение формальных моделей обычно производится путем последовательного выдвижения предположений (гипотез) о характере процессов, окружающей среды для сведения исходной задачи на естественном языке к одной из типовых схем моделирования. Причем степень адекватности гипотезы для конкретного объекта может изменяться во времени.

Выполнение всех этих гипотез обычно проверяется для каждого конкретного случая применения этой модели. Вполне естественно, что точное выполнение гипотез на практике отсутствует, а соответствующие количественные характеристики степени применимости модели для каждой конкретной ситуации отсутствуют и в модель объекта они не включаются. Между тем такие характеристики очень важны, особенно при наличии нескольких моделей или многоуровневой системы моделей и необходимости их согласования и координации. В данном случае в качестве языка, позволяющего провести согласование в условиях неопределенности и многоуровневости моделей, применяется теория нечетких множеств.

Пусть решение по каждой из mмоделй задано нечетким множеством D_i на множестве решений Y, тогда согласованное решение Dможет быть представлено как пересечение частных решений

Для каждого нечеткого решения D_i будет задаваться функция принадлежности .

После нахождения системного решения могут быть скорректированы ( скоординированы) исходные функции принадлежности.

Коррекция исходных нечетких величин

В общем случае задача коррекции исходных нечетких величин записывается следующим образом. Пусть имеется системное нечеткое решение

,

полученное в результате согласования нечетких решений и для моделей 1 и 2.

Исходные нечеткие параметры для модели 1 заданы функциями , для которых определено, что

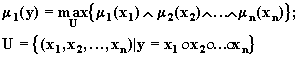
где o - арифметическая операция.

Необходимо получить скорректированные функции , для которых выполняется условие

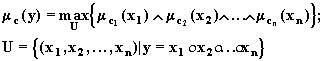
Алгоритм решения достаточно рассмотреть для случая n=2, поскольку для n>2 процесс коррекции сводится к последовательному применению данного простейшего алгоритма.

Пусть

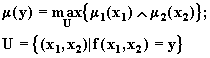(5.35)

,

где - корректирующая функция (например, функция предпочтения центра).

1. Для произвольного фиксированного y⁰ находим решение из системы уравнений

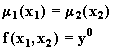
Если соотношение распадается на несколько зависимостей то выбирается та, для которой выполняется (5.35).

2. Полагаем

.

Тогда справедливо равенство

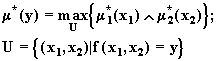
Обозначим

(5.36)

,

тогда

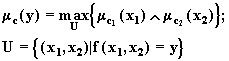
На основе данного метода нетрудно построить численные процедуры коррекции.

Коррекция по носителю

Для проведения коррекции по носителю для выбранных числовых значений y₁, y₂, ..., y_n используется приведенный выше метод коррекции, который в этом случае может быть сокращен, так как отпадает необходимость выполнения 3-го этапа. Это происходит потому, что y_i можно задавать только на , поскольку . Более того, если , то y_i задается в той части носителя, где .

Коррекция по r-уровням

Разобьем интервал на m r-уровней точками r_i, i=1,m. Из решения уравнений определяются r _i-уровненвые множества .

Находятся r_i -уровненвые множества для функции и из решения двух систем уравнений

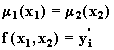(5.37)

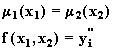(5.38)

откуда

где - решения систем уравнений (5.37) и (5.38) соответственно.

Поскольку и известны, то из (5.36) находятся r_i -уровненвые множества для и .

Алгоритм также можно упростить, если разбивать r _i-уровнями интервал [0, a ], где

и решать m систем

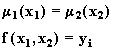
где y _i определяется из уравнения .

Если функции и заданы не аналитически, а дискретно по r_i -уровням, то в алгоритме коррекции первые два пункта не выполняются, а третий пункт изменяется следующим образом. Для нахождения r_i -уровневых множеств функций и функциональная зависимость

линеаризуется для соответствующего r_i -уровня. Тогда уравнения (5.37) и (5.38) принимают следующий вид:

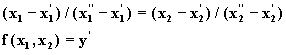
и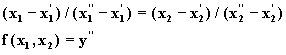

Причем, для выполняются следующие равенства

Уравнения при дискретном задании функций и можно аппроксимировать и нелинейной зависимостью, однако для практических расчетов линейная аппроксимация дает достаточно приемлемые результаты.

[К предыдущей главе].....[К содержанию] ......[К следующей главе]