6.1. Характеристика задач нечеткого математического программирования

Классическое математическое программирование и его разновидности - в значительной степени нормативная методология эффективного выбора. Нечеткое же программирование выделяет естественную множественность неточно определенных целей, значений и ограничений. При этом оптимальность определяется и в терминах поведения, и как качество, присущее решению.

Главная цель нечеткого математического программирования (НМП) - помочь лицу, принимающему решение, разобраться в выдвинутых им допущениях. Нечеткий подход не подменяет собой простейшего анализа в поисках разумной точности. Он облегчает задачу лица, принимающего решения, позволяя ему не формулировать явно точные ограничения. Вот почему плодотворный обмен идеями между теорией нечетких множеств и классическим программированием может явиться значительным шагом к созданию новых методов.

Стандартная задача нечеткого математического программирования формулируется обычно как задача максимизации (или минимизации) заданной функции на заданном множестве допустимых альтернатив, которое описывается системой равенств или неравенств. Например:

,

где Х - заданное множество альтернатив, и - заданные функции.

При моделировании в нечеткой форме реальных задач принятия решений в распоряжении исследователя - математика могут оказаться лишь нечеткие описания функции f и j , параметров, от которых зависят эти функции, да и самого множества Х. Таким образом, задача стандартного математического программирования превратится в задачу нечеткого математического программирования.

Формы нечеткого описания исходной информации в задачах принятия решений могут быть различными; отсюда и различия в математических формулировках соответствующих задач нечеткого математического программирования.

Перечислим некоторые из таких постановок [179].

Задача 1. Максимизация заданной обычной функции на заданном нечетком множестве допустимых альтернатив .

Задача 2. Нечеткий вариант стандартной задачи математического программирования. Пусть определена следующая задача математического программирования:

Нечеткий вариант этой задачи получается, если “смягчить” ограничения, т.е. допустить возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации функции f(х) можно стремиться к достижению некоторого заданного значения этой функции, причем различным отклонениям значения функции от этой величины приписывать различные степени допустимости.

Задача 3. Нечетко описана “максимизируемая” функция, т.е. задано отображение ,где Х - универсальное множество альтернатив, - числовая ось.

В этом случае функция при каждом фиксированном представляет собой нечеткое описание оценки результата выбора альтернативы (нечеткую оценку альтернативы ) или нечетко известную реакцию управляемой системы на управление . Задано так же нечеткое множество допустимых альтернатив .

Задача 4. Заданы обычная максимизируемая функция и система ограничений вида , причем параметры в описаниях функций заданы в форме нечетких множеств.

Задача 5. Нечетко описаны как параметры функций,определяющих ограничения задачи, так и самой максимизируемой функции.

Рассмотрим, например подробнее задачу линейного программирования с нечёткими коэффициентами. Нечеткость в постановке задачи математического программирования может содержаться как в описании множества альтернатив, так и в описании целевой функции.

(6.1)

На практике часто сталкиваются с применением точной теории оптимизации к неточным моделям, где нет оснований писать точно определенные числа и где слишком часто появляются трудности вычислительного характера при описании больших систем.

Нечеткую обстановку можно рассматривать как множество Х альтернатив вместе с его нечеткими подмножествами, представляющими собой нечетко сформулированные критерии (цели и ограничения), т.е. как систему (Х, f₀, f₁, ..., f_n). Принять во внимание по возможности все критерии в такой задаче означает построить функцию

D = f₀ f₁ ... f_n, (6.2)

в которую цели и ограничения входят одинаковым образом.

Решение можно определить как нечеткое подмножество универсального множества альтернатив. Оптимум соответствует той области Х , элементы которой максимизируют D. Это и есть случай нечеткого математического программирования.

Очевидно, неразумно в реальных ситуациях проводить резкую границу для множества допустимых альтернатив, поскольку может случится так, что распределения, лежащие за этой границей, дадут эффект, превышающий меньшую желательность для лица принимающего решения.

Например, ясно, что при несовместных распределениях эта область пустая. В этом случае налицо необходимость модификации ограничений. Желательно выяснить, как изменить ограничения задачи, чтобы появились допустимые решения и задача стала разрешимой.

В таких случаях представляется целесообразным вводить нечеткое множество допустимых элементов и, следовательно, рассматривать проблему как задачу НМП с применением подхода, дающего человеку больше свободы в использовании его субъективных представлений о ситуации.

Формы нечеткого описания исходной информации в задачах принятия решений могут быть различными; отсюда и различия в математических формулировках соответствующих задач НМП.

Нечеткий вариант стандартной задачи математического программирования получается, если "смягчить" ограничения, т.е. допустить возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации целевой функции f(x) можно стремиться к достижению некоторого заданного ее значения, причем различным отклонениям значения f(x) от этой величины приписывать различные степени допустимости (например, чем больше отклонение, тем меньше степень его допустимости).

Пусть а - заданная величина функции цели f(x), достижение которой считается достаточным для выполнения цели принятия решений, и пусть имеется пороговый уровень b такой, что неравенство f(x) < a-b означает сильное нарушение неравенства f(x) a. Тогда функцию принадлежности для нечеткой функции цели можно определить следующим образом:

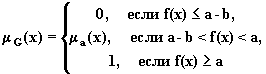(6.3)

где m _а - функция принадлежности, описывающая степени выполнения соответствующего неравенства с точки зрения лица, принимающего решения.

Аналогично определяется функция принадлежности для нечетких ограничений. В результате исходная задача оказывается сформулированной в форме задачи выполнения нечетко определенной цели, к которой применим подход Беллмана - Заде (6.2).

При моделировании ситуации в форме задачи линейного программирования

(6.4)

о коэффициентах a_ij, b_i иc_i известно лишь то, что они находятся в некотором множестве, отражающем все реальные возможности.

В некоторых случаях точное описанное множество ограничений (допустимых альтернатив) может оказаться лишь приближением реальности в том смысле, что в реальной задаче альтернативы вне множества ограничений могут не допустимыми, а лишь в той или иной степени менее желательными для лица, принимающего решения, чем альтернативы внутри этого множества.

Рассмотрим задачу нахождения минимума на заданной области. Пусть задана область вида:

, (6.5)

где - нечеткие подмножества множества R, а бинарная операция + обозначает сложение нечетких множеств.

Требуется найти на заданной области.

Коэффициент при каждой переменной в ограничениях можно считать функцией полезности, определенной на числовой оси. Можно считать, что эти коэффициенты дают субъективную оценку различных возможностей, включая таким образом другие, не определенные ограничения.

Сведём решение исходной задачи к решению ряда задач линейного программирования. Для этого введём дискретные a -уровни. В результате нечёткие ограничения принимают следующий интервальный вид:

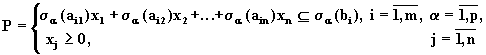(6.6)

Т.о., мы перешли от нечётких множеств к чётко определённым и теперь, зная, что s- обычный интервал, можем записать нашу задачу в следующем виде (случай 2? 2 ) :

(а₁₁ , а₁₂) x₁ + (c₁₁, с ₁₂) x₂ (b₁₁ , b₁₂)

(а₂₁ , а₂₂) x₁ + (с₂₁, с₂₂) x₂ (b₂₁ , b ₂₂) (6.7)

Теперь, чтобы привести задачу к виду обычной задаче линейного программирования, нам достаточно записать неравенства отдельно по левому и правому краям интервалов, с учётом знаков неравенства. Т.е., мы приведём систему к следующему виду :

а ₁₁x₁ + с₁₁x₂ b₁₁

a ₁₂x₁ + c₁₂x ₂ b₁₂ (6.8)

a₂₁x₁ + c₂₁x₂ b₂₁

a₂₂x ₁ + c₂₂x₂ b₂₂

С помощью несложных преобразований мы перешли от задачи с нечёткими коэффициентами к задаче линейного программирования с чёткими коэффициентами , при этом количество ограничений увеличилось в два раза и полученную задачу мы можем решить симплексным методом.

Таким образом, из рассмотренного примера явно просматривается алгоритм решения задачи с нечеткими коэффициентами. Следуя ходу рассуждений в данном примере, составим алгоритм решения задачи. Он имеет вид:

Как видим, исходная задача НМП представляется в виде совокупности обычных задач линейного программирования на всевозможных множествах уровня множества допустимых альтернатив. Если альтернатива х₀ есть решение задачи на множестве уровня a , то можно считать что число a есть степень принадлежности альтернативы х₀ нечеткому множеству решений исходной задачи. Перебрав таким образом всевозможные значения a , получаем функцию принадлежности нечеткого решения.

Если же и компоненты целевой функции с_i являются нечеткими, то необходимо выбирать для каждого уровня a соответствующие границы множеств в соответствии с правилами интервальной арифметики, минимизируя предварительно таким образом .

Из данного примера видно, что за гибкость приходится платить ценой увеличения размерности задачи. Фактически исходная задача с ограничениями по включению преобразуется в задачу с ограничениями в виде неравенств, с которыми легко обращаться; при этом такая цена не слишком высока, поскольку сохраняется возможность использования хорошо разработанных классических методов.

6.2. Численные методы решения задач нелинейного, линейного, нечеткого и интервального программирования

В реальной жизни мы чаще сталкиваемся со сложными системами, имеющими иерархическую структуру. Размерность таких задач, как правило, бывает очень велика, что создает трудности для применения к подобным системам симплекс-метода. Решение таких систем симплекс-методом без их преобразования - это очень трудоемкая процедура, которая к тому же даже на современных вычислительных машинах занимает много времени. Это делает практически невозможным решение таких задач без специальных методов.

Поэтому к таким системам обычно применяют методы декомпозиции, т.е. “большую” задачу разбивают на необходимое число меньших подзадач и решают симплекс-методом уже ее подзадачи, а затем сводят к решению первоначальной задачи.

В таком подходе тоже есть свои сложности, потому что не всякая система может быть разбита на подзадачи. Это налагает определенные ограничения и требования на исходную задачу и возможность решения задачи зависит от структуры матрицы задачи.

Существуют различные виды декомпозиционных методов в соответствии со структурой матрицы ограничений А.Наиболее часто встречающаяся структура, поддающаяся разложению, - это так называемая блочно-диагональная система, которая представляет собой серию блочно-диагональных подматриц, связанных группой ограничений общего вида, а именно:

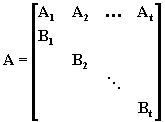
Задача с такой структурой матрицы ограничений может быть записана следующим образом:

максимизировать (6.9)

при условиях (6.10)

(6.11)

Такая структура возникает естественным образом в моделях, которые описывают процесс, разбитый на несколько стадий, когда ограничения заключают в себе все ограничения, относящиеся к периоду k=1,...,t, а группа связывающих ограничений относится к условиям, имеющим силу в течение всего планового периода. Описанная выше структура возникает также при моделировании иерархических систем, где каждая полуавтономная система имеет свои собственные ограничения и в то же время подчиняется доминирующим организационным ограничениям . Ясно, что, если каким-то образом избавиться от связывающих ограничений, задачу можно решить, решив t меньших подзадач.

Метод Данцига-Вулфа , разработанный для достижения этой цели, основан на понятии генерации столбцов, которое означает, что небазисные столбцы матрицы А, необходимые для вычисления относительных оценок, генерируются только по мере необходимости.

Предположим, что множество точек , удовлетворяющих ограничениям , является замкнутым и ограниченным (мы можем всегда обеспечить замкнутость и ограниченность множества, наложив соответствующее ограничение сверху на каждый элемент ). Тогда еще одна фундаментальная концепция, используемая в методе Данцига-Вулфа, заключается в том, что любая точка множества может быть представлена в виде

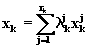(6.12)

где 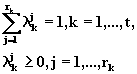(6.13)

а - вершины (крайние точки) множества .

Мы можем, следовательно, переформулировать исходную задачу (6.9)-(6.11) в виде: из всех решений, определяемых соотношениями (6.11), найти те, которые удовлетворяют уравнению (6.10) и максимизируют .

Используя равенство (6.12) , выражение (6.9) преобразуем к виду:

максимизировать , (6.14)

а уравнение (6.10) к виду

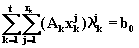(6.15)

Если мы определим

и ,

тогда выражения (6.12)-(6.15) определят задачу линейного программирования относительно переменных , называемую координирующей задачей :

максимизировать 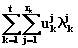(6.16)

при условиях 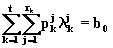(6.17)

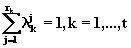(6.18)

Отметим, что эта задача имеет только , строк, в то время как исходная задача имела строк; таким образом мы получаем значительную потенциальную экономию. Назначение координирующей задачи - приписать соответствующие весовые коэффициенты решениям , удовлетворяющим соотношениям (6.11) .

Однако число столбцов координирующей задачи равно числу вершин множества , k = 1,...,t, которое может быть очень велико. Поэтому для решения исходной задачи мы используем метод генерации столбцов, создавая их по мере необходимости.

Предположим, что решая координирующую задачу, мы вычислили вектор оценок ограничений и теперь нам нужен небазисный столбец для вычисления его относительной оценки.

Относительная оценка небазисного столбца, соответствующего переменной ,равна

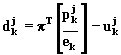
Разбив вектор на части , отвечающие уравнениям (6.11), мы можем представить в виде:

Поиск наиболее отрицательной относительной оценки эквивалентен решению задачи линейного программирования, называемой k-й подзадачей:

максимизировать (6.19)

при условиях (6.20)

Решение, которое обозначим через , будет крайней точкой множества и будет соответствовать наиболее отрицательной относительной оценке. Таким образом, мы сгенерируем требуемый столбец

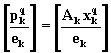
который теперь можно ввести в базис координирующей задачи, а соответствующий коэффициент целевой функции определим по формуле .

Этот процесс повторяется для всех k=1,...,t, и решение, соответствующее наиболее отрицательной относительной оценке среди всех k подзадач, определяет столбец для ввода в базис координирующей задачи; выполнение последующих шагов симплекс-метода приведет к вычислению нового вектора относительных оценок на следующей итерации.

В качестве альтернатив решению каждой подзадачи в отдельности можно осуществлять агрегирование, определив

и

Тогда координирующая задача будет иметь строк вместо и только одну подзадачу:

максимизировать (6.21)

при условиях (6.22)

Эта задача может быть решена решением t индивидуальных подзадач с последующим агрегированием их решений.

Преимущество первого варианта решения задачи (6.16)-(6.18) - его гибкость; плата за эту гибкость - лишние (t-1) строк в координирующей задаче.

Существующие вычислительные алгоритмы решения задач нелинейного программирования можно подразделить на следующие группы:

1. Применение аппарата линейного программирования для задач нелинейного программирования путем использования процедуры последовательной линейной аппроксимации [233]. Применяются также методы квадратичной аппроксимации [122] с решением на каждом шаге задачи квадратичного программирования.

2. Декомпозиция задачи нелинейного программирования с ограничениями в эквивалентную ей последовательность простых задач (например, безусловной оптимизации) путем введения в рассмотрение штрафных функций и т.д. [233].

3. Применение интервальной и нечеткой арифметики, позволяющей оперировать в процессе решения задач оптимизации с областями допустимых и нечетких решений (с изменяющейся степенью допустимости решения) [134, 166].

4. Покомпонентная релаксация, когда уменьшение невязок сетевых уравнений производится их последовательной обработкой по отдельным уравнениям и переменным.

Описание, потенциальные возможности и сравнительный анализ ряда существующих методов и пакетов программ для ЭВМ по решению задач нелинейного программирования приведены в работах [233, 280]. Сравнительный анализ и рекомендации по условиям применимости этих пакетов сделаны с учетом следующих характеристик: точность, быстродействие, сходимость, размерность решаемых задач, эффективность работы, ограничение на число переменных и ограничений, наличие сервисных средств (ввода описаний, редактирования, использования отображения в графической форме процесса сходимости и т.д.) [280].

Методы линейной аппроксимации. Наличие ППП для решения задач линейного программирования большой размерности при наличии ограничений-равенств и ограничений-неравенств линейной структуры привело к созданию большого числа методов решения задач нелинейного программирования с помощью процедуры линеаризации с применением итерационного процесса. В этом случае задача нелинейного программирования в общей постановке

, (6.23)

при ограничениях

; (6.24)

; (6.25)

может быть модифицирована путем записи каждой из нелинейных функций этой задачи двумя первыми числами в соответствующем разложении в ряд Тейлора в окрестности и сведена к задаче линейного программирования:

; (6.26)

при ограничениях

; (6.27)

. (6.28)

Сходимость этих методов к решению гарантируется, если [40] :

1) являются непрерывными и дифференцируемыми функциями ;

2) функция выпуклая, а выпуклая в допустимой области D;

3) представляют собой вогнутые функции;

4) множество D замкнутое, выпуклое и непустое;

5) все фигурирующие в условиях функции ограничены.

При отсутствии выполнения условий 1-5 алгоритмы, использующие методы линейной аппроксимации, позволяют найти локальный оптимум.

Задача линейного программирования (ЛП) с целью координации решений и учета допущений дополняется условием, ограничивающим длину шага при перемещении в том или ином направлении малой величиной

. (6.29)

Полученное решение задачи (6.26)-(6.28) дает возможность вычислить следующую точку

. (6.30)

Повторением приведенной выше процедуры при постепенном уменьшении достигают такой ситуации, когда минимизирующая поправка к найденному на предыдущем шаге значению оказывается меньше наперед заданного числа. В случае, когда начальный вектор оказывается вне пределов допустимой области D, вводятся искусственные переменные , добавляемые в ограничения равенства и неравенства.

Принадлежащий к этому классу алгоритмов метод обобщенного приведенного градиента (GRG) применяется в алгоритмах оптимизации работы газопровода [146]. В качестве достоинств этого метода отмечаются:

- простота формулировки целевой функции для трубопровода как функции независимых и зависимых переменных;

- возможность получения допустимого решения на каждой итерации за счет перемен местами зависимых и независимых переменных;

- устойчивость алгоритма к нарушению исходных предпосылок и его надежность;

- оптимальные решения находятся даже при больших интервалах задания начальных условий.

Однако этот метод успешно применяется только при решении задач с непрерывной и дифференцируемой по управляющим переменным функцией цели, когда параметры в задаче имеют непрерывные диапазоны.

Когда управляющие или координирующие параметры имеют дискретные значения (например, при выборе схемы включения ГПА на КС) используются другие методы, например, динамическое программирование [53, 146]. Декомпозиция задач позволяет использовать при решении каждой локальной задачи тот метод, который наиболее эффективен для данной ситуации. Так в работе [146] для оптимизации режима работы газопровода в целом используется метод ПКП, а для оптимизации режима работы КС - динамическое программирование.

Декомпозиционные методы.

Принцип параметрической декомпозиции. Производится фиксация r параметров и решается основная задача (6.23)

(6.31)

, (6.32)

размерность которой сокращается на r [90]. В результате решения этой задачи линейного программирования находятся базисные, небазисные переменные и двойственные оценки для ограничений (6.31). После этого решается вторая задача

(6.33)

при ограничениях

; (6.34)

.

Все небазисные переменные в (6.34), найденные при решении задачи (6.31)-(6.32) приравниваются нулю, осуществляется линейная аппроксимация ограничений (6.34) (иногда и целевой функции) и решается полученная задача (например, методом проекции градиента [90]). Решение задачи (6.33)-(6.34) используется для нахождения нового решения задачи (6.31)-(6.32) и процедура повторяется , пока не будет достигнута заданная точность решения.

Одним из примеров интерактивной оптимизации является метод крупноформатных электронных таблиц (КЭТ) [226], который представляет собой выгодную альтернативу алгоритмам линейного программирования.

Проведение структурной декомпозиции исходной задачи путем линеаризации исходной модели позволяет использовать новый класс моделей - линейных моделей с переменными коэффициентами.

Применение этих моделей дает возможность решить задачу следующего вида [90] :

; (6.35)

;

. (6.36)

где - заданные функции управлений .

Такую модель можно записать, когда работа каждого элемента описывается линейной моделью с переменными коэффициентами вида

(6.37)

. (6.38)

Модели элементов (агрегатов) вида (6.37)-(6.38) имеют широкую область применения в нефтехимии [90], электроэнергетике и т.д. Модель отдельного элемента (агрегата) можно рассматривать как результат линеаризации нелинейной модели

(6.39)

по входным параметрам , например, путем разложения функции в ряд Тейлора в окрестности некоторого значения входных параметров и пренебрегая в этом разложении членами второго порядка и выше [90].

Для аппроксимации производственных возможностей агрегатов, допускающих различные режимы работы внутри интервала , используется понятие граничного режима [90]. Промежуточные режимы представляются как линейные комбинации граничных. Граничные режимы характеризуют предельно возможные условия работы технологических агрегатов. Путем последовательной фиксации значения в интервале для каждого из этих значений с использованием принципа параметрической декомпозиции можно получить последовательность оптимальных значений функционала F и затем выбрать решение, дающее наименьшее значение F.

Иногда для моделирования сложных процессов применяются диапазонные моделивида [90]

; (6.40)

;

где - векторы; - матрицы коэффициентов; - векторы входных и выходных потоков объекта; - вектор переменных, обеспечивающих диапазонную зависимость выходов и входов.

Сведение задач к стандартным задачам по решению систем линейных уравнений, линейного программирования позволяет воспользоваться хорошо разработанными стандартными алгоритмами и программами [153, 193, 224], для которых определены условия существования и сходимости решений. Вопросы количественной оценки степени обусловленности для ряда задач даны в работе [193].

В качестве численных методов решения системы алгебраических уравнений вида

(6.41)

применяются метод Ньютона-Рафсона и алгоритмы работы с симметричными разреженными матрицами - метод -факторизации и метод автоматической перенумерации узлов [175, 177] . Метод перенумерации узлов обеспечивает минимум ширины ленты матрицы , а метод -факторизации - возможность представления матрицы в виде

. (6.42)

Тогда (6.41) может быть записано в виде

; (6.43)

. (6.44)

Сначала решается уравнение (6.43) относительно , затем (6.44) относительно [98].

Имеются также методы параллельного решения на N процессорах систем линейных алгебраических уравнений [167].

В случае наличия ошибок замеров параметров в уравнении (6.41) вместо истинных параметров могут замеряться искаженные ошибками значения . То есть, возникает необходимость найти последовательность решений , сходящуюся к истинному решению , на основе последовательности , сходящейся к истинным данным . Однако решения в этом случае будут неустойчивыми, так как обратный оператор в общем случае не ограничен (а иногда может не существовать).

Ввиду того, что небольшие изменения значений исходных данных могут привести к значительным отклонениям в решении, эта задача относится к классу некорректных задач [81, 138, 165].

Основными методами решения некорректных задач являются [81]:

- метод регуляризации А.Н.Тихонова;

- метод статистической регуляризации;

- прямые и итерационные методы.

Рассмотрим регуляризацию функционала

, (6.45)

где Е и Х - пространства данных и решений соответственно.

Тогда согласно теореме, доказанной в [302], если сходится к в Е, а последовательность положительных чисел выбрана так, что

при ,

существует последовательность ( выпуклое замкнутое подмножество Х) такая, что

а) , (6.46)

б) сильно сходится к в Х.

Эти результаты можно использовать для решения задач идентификации распределенных систем. В этом случае задача идентификации будет трактоваться как задача оптимизации некоторых квадратичных функционалов [302].

Задача вида (6.45) может быть использована и для идентификации параметров моделей. В этом случае вместо записывается выражение для оцениваемых параметров L. Задача оценивания может быть поставлена и для более сложного случая, когда - то есть, одновременно необходимо и оценивать параметры состояния и уточнять коэффициенты моделей . В этом случае задача оценивания может быть сведена к определению значений и в двухэтапной задаче оптимизации [326]

, (6.47)

при условиях, определяемых системой уравнений (6.46).

Для определения параметра регуляризации l используется целый ряд методов [165]. Они основаны на оценивании параметра регуляризации l из дополнительного условия

, (6.48)

где y - нелинейный функционал, определенный на решениях задачи (6.45), а - априори задаваемый уровень допустимых значений функционала y .

В работе [352] рассмотрены три способа выбора параметров регуляризации :

(принцип невязки) (6.49)

(принцип квазирешений) (6.50)

(6.51)

(принцип сглаживающего функционала).

Величина характеризует задаваемый уровень невязки и определяется по методу невязки. Величина связана с априорными сведениями о размере области, в которой находится искомое решение, и определяется методом квазирешений. Величина практически выбирается из тех же соображений , что и .

Если , , принадлежат множествам значений функций r , g и j , то уравнения (6.49) - (6.51) однозначно разрешимы [165].

Это связано с тем , что функции , и непрерывны при , причем и строго монотонно возрастают , а строго монотонно убывает. В той же работе приводятся модификации этих уравнений, к которым применимы быстро сходящиеся алгоритмы ньютоновского типа.

Из детерминированных методов неплохо зарекомендовал себя при параметрической идентификации метод наименьших квадратов с использованием теории чувствительности [108], который заключается в определении отклонения фактических параметров

от их номинальных значений в предположении, что величина является малой. Для решения этим методом задач балансирования потоков газа и идентификации коэффициентов моделей такое предположение является естественным ввиду монотонного характера изменения коэффициентов эффективности для линейных участков (ЛУ) и незначительного изменения потоков газа в магистральных газотранспортных сетях между проводимыми часовыми и суточными расчетами.

Однако из-за некорректности задачи (замеры давления имеются не во всех вершинах сети) осуществляется минимизация функционала J вида (6.45) с регуляризующей добавкой.

Переменные в условиях малых отклонений от номинальных могут быть представлены приближенно в виде

, (6.52)

где 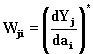- функция чувствительности переменной по параметру , причем * - означает, что производные или переменные вычисляются при номинальных значениях параметров. Переменные определяются из решения заданной системы уравнений при номинальных значениях параметров , а функции чувствительности находятся из решения системы линейных уравнений

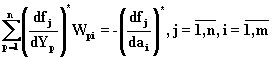. (6.53)

Далее из условий минимума квадратической формы вида

(6.54)

находятся по методу наименьших квадратов оценки параметров , а по ним и новые значения параметров

(6.55)

После этого проверяется критерий окончания счета

, (6.56)

где e - заданная точность оценки параметров. Если условие (6.56) выполняется, то расчет считается законченным, если нет - полученные оценки принимаются как номинальные и расчет повторяется.

Вопросы существования и единственности решения для этого метода обсуждаются в [108,стр.260]. Этот метод может также применяться и при наличии одновременно L замеров для всех переменных. В этом случае квадратическая форма Ф выглядит следующим образом:

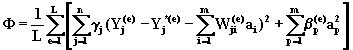. (6.57)

Величины определяются с использованием рекомендаций теории чувствительности, а весовые коэффициенты g могут выбираться равными обратным значениям дисперсий измерений [108]. Конкретные примеры по выбору и приведены для различных задач газотранспортных сетей в работе [30].

Использование нескольких последовательных замеров режимов работы сети газопроводов приводит к переходу от недоопределенной к переопределенной системе узловых уравнений [153]. Однако если удастся получить замеры лишь незначительно отличающихся друг от друга режимов, то это может привести к плохой обусловленности матрицы нормальной системы уравнений.

Применение сложных нестационарных моделей требует больших дополнительных объемов исходной информации, которую либо готовит диспетчерский персонал, либо она собирается с помощью телеметрии.

Однако низкая точность этой дополнительной информации, отсутствие целого ряда дополнительных датчиков, сложность комплексной проверки вводимой информации заставляет разработчиков АСДУ искать принципиально новые подходы к моделированию режимов, например, использовать функции чувствительности энергосистем [148].

На этих же идеях теории чувствительности построен алгоритм регулирования напряжения и мощности в энергетических системах иерархической структуры [258]. С использованием ЭВМ первого уровня иерархии осуществляют регулирование напряжения и мощности в пределах подсистем в предположении линейной зависимости связывающих отклонения регулируемых параметров с отклонениями параметров режима регулирующих устройств с учетом соответствующих матриц чувствительности S

, (6.58)

где - отклонения параметров, вызванные изменениями нагрузок. ЭВМ вышестоящего уровня осуществляет координацию потоков с учетом связей отдельных подсистем.

Накопленный в электроэнергетике опыт показывает эффективность и достаточную точность анализа чувствительности при решении задач диспетчерского управления режимами и связанных с ними оптимизационных проблем [150 ]. Представленный в работах Тиннея В.Ф. и Доммела Г.В. [150] обобщенный метод для вычисления чувствительности одной или нескольких зависимых переменных или некоторой целевой функции к изменению некоторого подмножества специально выбранных параметров электроэнергетической системы, использует линейное приближение и в условиях нормальных режимов является достаточно точным. Однако даже в условиях, значительно отличающихся от нормальных, знак и величина коэффициентов чувствительности могут оказаться полезной информацией, указывающей на признаки аварийной ситуации [ 150]. Для улучшения сходимости могут использоваться понятия нечеткой чувствительности при наличии нечетко заданных замеров и коэффициентов уравнений [170].

[К предыдущей главе].....[К содержанию] ......[К следующей главе]