6.3. Игры в нечетко определенной обстановке
Во многих прикладных областях часто встречаются ситуации, в которых выполнение цели или результаты принятия решений одним лицом зависят не только от его действий, но и от действий другого лица или группы лиц, преследующих свои собственные цели. Рассмотренный подход к задачам принятия решений можно применять и для анализа подобных игровых ситуаций в нечетко определенной обстановке. Формулируется такая игра следующим образом.
Пусть X и Y - множества элементов,
которые могут выбирать игроки 1 и 2
соответственно. Допустимые выборы
(стратегии) игроков 1 и 2 описываются
нечеткими множествами С1 и С2 в X и Y соответственно с
функциями принадлежности ![]() и
и ![]() . Заданы
также функции
. Заданы
также функции ![]() , причем значение
, причем значение ![]() есть
оценка игроком i ситуации (х,у) без учета допустимости
выборов х и у. Цель игрока i
описывается
нечетким множеством Gi в R c функцией
принадлежности
есть
оценка игроком i ситуации (х,у) без учета допустимости
выборов х и у. Цель игрока i
описывается
нечетким множеством Gi в R c функцией
принадлежности ![]() . Следует заметить, что
цель, поставленная игроком, может
оказаться плохо или вообще
несовместимой с его возможностями,
т.е. с множеством его стратегий.
. Следует заметить, что
цель, поставленная игроком, может
оказаться плохо или вообще
несовместимой с его возможностями,
т.е. с множеством его стратегий.
Целью игрока i можно считать нечеткое множество в X* Y с функцией принадлежности
![]() .
(6.59)
.
(6.59)
Образом этого нечеткого множества при отображении fi является заданное нечеткое множество цели игрока i.
Введем нечеткие множества D 1и D2 в X* Y, определив их функции принадлежности следующим образом:
![]() (6.60)
(6.60)
![]()
Смысл нечетких
множеств D1и D 2 можно пояснить
следующим образом. Если, например,
игроку 1, известен конкретный выбор у* игроком 2, то перед ним
стоит задача достижения нечеткой
цели![]() при множестве допустимых
альтернатив
при множестве допустимых
альтернатив ![]() . В соответствии с
используемым здесь подходом
Беллмана - Заде решение D1
такой задачи
определяется как пересечение
нечетких множеств цели и
ограничения:
. В соответствии с
используемым здесь подходом
Беллмана - Заде решение D1
такой задачи
определяется как пересечение
нечетких множеств цели и
ограничения:
![]() .
(6.61)
.
(6.61)
Таким образом,
нечеткое множество D1
можно
рассматривать как семейство (по
параметру у) решений задач
достижения нечетких целей ![]() .
Аналогичный смысл придается и
множеству D 2.
.
Аналогичный смысл придается и
множеству D 2.
Далее будем
считать, что при каждом
фиксированном выборе одного игрока
второй выбирает стратегию, которая
максимизирует соответствующую ему
функцию ![]() .
.
Если игрок полагается целиком лишь на свои возможности, то естественной является его ориентация на получение наибольшего гарантированного выигрыша, т.е. рациональным считается такой способ оценки игроком 1 своих выборов, при котором он рассчитывает на наихудшую для него реакцию игрока 2 из множества возможных реакций последнего.
При этом важную роль играет имеющаяся в его распоряжении информация об интересах и ограничениях игрока 2. Если, например, игрок 1 имеет возможность первым выбрать свою стратегию, а игроку 2 становится известным этот выбор, то наибольший гарантированный выигрыш игрока 1 равен
![]() (6.62)
(6.62)
Присутствующее в этом выражении множества Y(x), зависящего от х, есть множество возможных реакций (ответов) игрока 2 на выбор х игрока 1. В этом смысле зависимость Y(x) отражает степень информированности игрока 1 об интересах и ограничениях игрока 2.
Если величина H1 слишком мала, то это означает, что цель, к выполнению которой стремится игрок 1, слишком завышена (с учетом его возможностей). В связи с этим естественным образом возникает следующая задача. Каково должно быть нечеткое множество стратегий игрока 1, которое гарантировало бы ему (при заданной информированности об игроке 2) достижение цели со степенью, не меньшей некоторого заданного числа a ?
Для решения этой задачи введем множество
![]() (6.63)
(6.63)
Если ![]() , то
H1 < a, и следовательно,
игрок 1 не может гарантировать
достижение своей цели со степенью
большей или равной a независимо от того,
какое множество стратегий
находится в его распоряжении.
, то
H1 < a, и следовательно,
игрок 1 не может гарантировать
достижение своей цели со степенью
большей или равной a независимо от того,
какое множество стратегий
находится в его распоряжении.
Пусть ![]() , тогда
можно заключить, что гарантировать
достижение цели со степенью не
менее a можно только тогда,
когда
, тогда
можно заключить, что гарантировать
достижение цели со степенью не
менее a можно только тогда,
когда ![]() при некотором
при некотором ![]() .
.
6.4. Многошаговые процессы принятия решений
Для простоты будем полагать, что управляемая система А является инвариантной по времени детерминированной системой с конечным числом состояний. Именно, каждое состояние х t, в котором система А находится в момент времени t, t=0,1,2,..., принадлежит заданному конечному множеству возможных состояний Х= {s1,..., sn}; при этом входной сигнал в момент времени t является элементом множества U={a1,..., am}. Динамика системы во времени описывается уравнением состояния
![]() ,
(6.64)
,
(6.64)
в котором f - заданная функция,
отображающая X*U
в X. Таким образом, ![]() представляет собой последующее
состояние для хt при входном сигнале ut
. Считается также,
что заданы начальное состояние х0 и фиксированное время
окончание процесса N.
представляет собой последующее
состояние для хt при входном сигнале ut
. Считается также,
что заданы начальное состояние х0 и фиксированное время
окончание процесса N.
Предполагается,
что в каждый момент времени t на входную переменную
наложено нечеткое ограничение Сt, являющееся нечетким
множеством в U с функцией
принадлежности ![]() . Кроме того, считается,
что цель - нечеткое множество GN в Х, определяемое
функцией принадлежности
. Кроме того, считается,
что цель - нечеткое множество GN в Х, определяемое
функцией принадлежности ![]() . Задача заключается в
нахождении максимизирующего
решения.
. Задача заключается в
нахождении максимизирующего
решения.
Используя идеи п.5.1, можно записать решение как нечеткое множество в U* ...* U в виде
![]() (6.65)
(6.65)
где`GN - нечеткое множество в U* ...* U, индуцируемое GN в Х. Для функции принадлежности имеем
![]() (6.66)
(6.66)
где хN может быть выражено как функция от u 1,...,uN-1и х0 путем последовательного применения уравнения (6.64).
Для многошаговых процессов целесообразно представить решение в виде [54]:
![]()
где pt - принятая "стратегия" или правило выбора входного воздействия ut в зависимости от состояния системы хt.
Таким образом,
задача сводится к нахождению
оптимальных стратегий pt и соответствующей
последовательности входных
воздействий u1,...,uN-1
, максимизирующих ![]() в (6.66). Для решения
задачи применяется метод
динамического программирования.
Используя (6.64) и (6.65), имеем
в (6.66). Для решения
задачи применяется метод
динамического программирования.
Используя (6.64) и (6.65), имеем
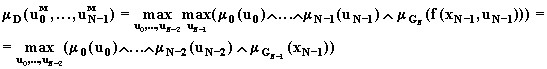 (6.67)
(6.67)
где ![]() (6.68)
(6.68)
может рассматриваться как функция принадлежности нечеткой цели в момент t = N-1, индуцированной заданной целью GN в момент t = N.
Повторяя процесс обратных итераций, получаем систему рекуррентных уравнений
![]()
![]() (6.69)
(6.69)
которая дает
решение задачи. Таким образом,
максимизирующее решение
получается последовательной
максимизацией величин ![]() в (6.69),
причем
в (6.69),
причем ![]() определяется как функция от
определяется как функция от ![]() .
.
В качестве простого примера рассмотрим систему с тремя состояниями s1, s 2 и s 3 и двумя входными сигналами a1 и a2. Пусть N=2 и нечеткая цель в момент времени t=2 определяется функцией принадлежности, принимающей значения
![]()
Пусть далее, нечеткие ограничения в моменты t=0 и t=1 задаются функциями
![]()
Допустим, что таблица изменения состояний, задающая функцию f в (6.64), имеет следующий вид
| s1 | s2 | s3 | |
| a1 | s1 | s3 | s1 |
| a2 | s2 | s1 | s3 |
Используя (6.69), находим функцию принадлежности нечеткой цели в момент t=1:
![]()
Соответствующее максимизирующее решение имеет вид
![]() .
.
Аналогично для t = 0 имеем
![]()
и ![]() .
.
Итак, если
начальное состояние в момент
времени t=0 есть
s 1, то максимизирующим
решением будет a2,
a1, причем
соответствующее значение функции
принадлежности ![]() равно 0,8.
равно 0,8.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]