6.5. Особенности контроля и управления в условиях стохастической неопределенности

При составлении проекта редко располагают необходимой для синтеза системы управления полной априорной информацией об объекте и окружающей его среде. Даже если известны системы уравнения, описывающие поведение системы, то часто оказывается, что нет данных о величине отдельных параметров и к тому же нередко имеющиеся модели слишком сложны. В дальнейшем оказывается, что принятая при проектировании модель существенно отличается от реального объекта, что значительно уменьшает эффективность разработанной системы управления. В связи с этим актуальной становится возможность уточнения модели на основе наблюдений, полученных в условиях нормального функционирования объекта.

Таким образом, задача идентификации формулируется следующим образом: по результатам наблюдений над входными и выходными переменными системы должна быть построена оптимальная в некотором смысле модель, т.е. формализованное представление этой системы.

В зависимости от априорной информации об объекте управления различают задачи идентификации в узком и широком смысле. В последнем случае приходится предварительно решать большое число дополнительных проблем. К ним относятся: выбор структуры системы и задание класса моделей, оценка степени стационарности и линейности объекта, степени и формы влияния входных воздействий на состояние, выбор информативных переменных и др. Задача идентификации в узком смысле состоит в оценке параметров и состояния системы по результатам наблюдений над входными и выходными переменными, полученными в условиях функционирования объекта. Для решения отмеченных проблем в современной теории управления обычно используют модели в пространстве состояний.

Проблеме построения алгоритмов управления объектами с неполной информацией в настоящее время уделяется большое внимание. Это объясняется прежде всего тем, что при создании систем управления сложными технологическими процессами обычно не располагают достоверными моделями объектов. Ни одна из существующих теорий не может претендовать на то, что единственно она дает правильное описание работы систем. Скорее имеется целый спектр теорий, трактующих эти проблемы. При имеющемся сейчас узком рассмотрении лишь отдельных процессов и только на определенных уровнях описания получается одностороннее представление о системе, не позволяющее иметь достоверные оценки обо всех процессах.

Поведение реальной системы характеризуется некоторой неопределенностью, причем при достаточно большом объеме информации об объекте внешнее возмущение, действующее на управляемый объект, можно представить как случайный процесс.

Стохастическое оптимальное управление в значительной степени базируется на основных положениях динамического программирования .

Для линейных систем с квадратичным критерием решение дается так называемой теоремой разделения, которая позволяет составлять оптимальную стратегию из двух частей: оптимального фильтра, который вычисляет оценки состояния в виде условного среднего при заданных наблюдениях выходных сигналов и линейной обратной связи. Оказывается, что линейная обратная связь может быть найдена путем решения задачи детерминированного управления. Оценка состояния характеризует выходную переменную фильтра Калмана, который по существу представляет математическую модель системы, когда управление осуществляется по наблюдениям. Таким образом, теорема разделения обеспечивает связь между теориями фильтрации и стохастического оптимального управления.

Описание многомерных динамических объектов. Под "состоянием" объекта понимают совокупность величин, полностью определяющих его положение в данный момент и играющих роль начальных условий для всего будущего движения. Такой путь описания, обладая рядом математических преимуществ, получил значительное распространение в анализе систем и особенно систем, подверженных случайным воздействиям.

Математические описания динамических объектов при случайных воздействиях внешне ничем не отличаются от соответствующего описания объектов в детерминированной постановке. Однако за внешним сходством скрываются существенные особенности, заключающиеся в том, что в этом случае, как вектор состояния, так и вектор выходных переменных объекта представляют собой случайные процессы, порождаемые либо случайными возмущениями на входе объекта, либо случайными начальными условиями, либо помехами в каналах измерений.

Выбор вектора состояния и вывод уравнения состояния являются начальным этапом разработки систем управления динамическими объектами, поскольку первичное описание объектов задается обычно в виде системы дифференциальных уравнений в частных производных.

Исследование условий наблюдаемости и идентифицируемости фильтров Калмана при моделировании процессов. Оптимальное управление, оценка и идентификация возможны только в том случае, когда имеет место управляемость, наблюдаемость и идентифицируемость. Поведение динамического объекта может описываться уравнением состояния

X _k+1=ФX _k+ГQ _k(6.70)

при следующей схеме измерений:

Y_k=HX_k , (6.71)

гдеY_k - т-вектор замеров (пластовых давлении); H[m:n]- матрица измерений.

В этом случае возникает вопрос: при каких условиях можно получить необходимую информацию о состоянии объекта, измеряя его выходные сигналы.

Таким образом, имеем

Y₀ =HX₀; (6.72)

Y₁=HX ₁=HФX ₀;

…

Y_n-1=HФ^n-1X₀

или транспонируя, получаем

(6.73)

Так как векторы Y известны, существует единственное решение X₀ , когда матрица

N=[H ^TФ^T H^T… (Ф ^T)^n-1H^T ] (6.74)

Имеет ранг n. В этом случае пара (Ф,Н) называется наблюдаемой. Тогда, если принять нестационарную систему

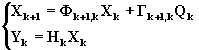(6.75)

квазистационарной на интервале дискретности T, то условия полной наблюдаемости системы (6.70) можно свести к нахождению ранга матриц N_k в опорных точках траектории коэффициентов матриц Ф _k, H_k, где k-количество опорных точек или интервалов дискретности. Естественно, при высоких размерностях вектора состояния решение этой задачи требует довольно сложных алгоритмов и значительного объема вычислений. Чтобы устранить эти затруднения, образуют новые матрицы наблюдаемостиW_k, в виде

W_k=N_k N_k^T, (8.76)

гдеW_k, - всегда квадратные матрицы размерностью n,n. Таким образом, оценка наблюдаемости многомерных нестационарных объектов может быть сведена к простой процедуре вычисления в опорных точках определителей матриц W_k,. При этом для полной наблюдаемости объекта необходимо, чтобы det W_k 0.

При построении адаптивных систем управления нестационарными объектами учет условий идентифицируемости, как и условий наблюдаемости, является принципиально необходимым. В противном случае задача не может быть решена или же будут получены неправильные результаты с физической точки зрения. Предполагая, что скорость изменения параметров нестационарной системы достаточно мала по сравнению со временем переходного процесса в системе, нестационарную систему можно заменить эквивалентной системой с кусочно-постоянными параметрами. Тогда условие идентифицируемости можно получить следующим образом:

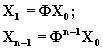(6.77)

или

[X₁ X₂ … X_n-1]= Ф[X₀Ф X₀… Ф ^n-1X₀]. (6.78)

Так как векторы X_i известны, существует единственное решение для Ф, когда матрица

V=[X₀ФX₀… Ф^n-1X₀ ] (6.79)

имеет ранг n.

Синтез алгоритмов оптимальной оценки состояния. При невозможности прямого измерения всех компонент вектора состояния, обычный классический подход к оценке методом наименьших квадратов приводит к использованию непоследовательных схем оценки, основной недостаток которых состоит в необходимости повторять полный расчет каждый раз, когда производится дополнительное наблюдение. Рекуррентные алгоритмы дают возможность уменьшить количество вычислительных операций и существенно упрощают программирование задач оценки. Алгоритм оптимальной в среднеквадратическом смысле оценки состояния динамической системы можно записать в виде

X_k+1,k+1=X_k+1,k+K _k+1(Y_k+1-H_k+1 -H_k+1X_k+1,k;

X _k+1,k=Ф _k+1,kX_k,k+ Г_k+1,kQ_k+G _k+1,km_k;

K_k+1 =F_k+1H^T_k+1 (H_k+1F_k+1,kH ^T_k+1+R_k+1) ^-1; (6.80)

F_k+1,k=Ф_k+1,kF _k,kФ^T _k+1,k+G_k+1,ke_k G^T_k+1,k;

F _k+1,k+1=(I-K_k+1H_k+1 )F_k+1,k.

Формулы (6.80) образуют рекуррентный алгоритм обработки измерений объекта управления. Новая оценка состояния строится как экстраполированная по уравнениям динамики системы, старая оценка плюс "взвешенная" разность между измерением выхода и прогнозом этого измерения на основании прошлых измерений". Для начала рекуррентной процедуры вычисления необходимы априорные сведения о ковариационных матрицах шумов e, R и начальном состоянии системы X_0,0иF₀.

Полученный алгоритм оценки состояния совпадает с фильтром Калмана, так как в основе алгоритмов лежит один и тот же критерий оптимальности и приняты те же самые ограничения.

Однако в отличие от существующих алгоритмов здесь рассматривается управляемое движение нестационарных объектов, и при этом учитываются ошибки измерений и нестационарность внешних возмущений.

Использование фильтров Калмана для оценки вектора X _k,kпредполагает наличие большой оперативной памяти ЭВМ и связано с методами декомпозиции исследуемого процесса. Поэтому для практических целей удобнее применять методы стохастической аппроксимации. Обозначим скалярный показатель качества идентификации определяемый в виде

(6.81)

Оценка вектора состояния получается из алгоритма стохастической аппроксимации следующим образом:

(6.82)

Для обеспечения сходимости последовательность р _k. должна удовлетворять условиям Дворецкого.

6.6. Контроль и управление динамическими системами в нечетких условиях

Применение стохастических методов для контроля и управления процессом в некоторых ситуациях оказывается затруднительным ввиду отсутствия вероятностных распределений параметров. Сложность получения численных результатов при работе со случайными величинами также снижает практическую ценность стохастических алгоритмов.

В случае неполной информации о сложном процессе удобнее представлять неточно заданные параметры в виде нечетких величин и при работе с ними пользоваться предложенными в данной работе методами.

Коэффициенты целого ряда моделей фактически зависят от многих факторов реального процесса, не учтенных в модели. При описании процессов двухмерными моделями мы заменяем по третьему измерению однородным слоем и значения коэффициентов для него определяем как среднее, средневзвешенное и т.д. Попытка внесения в модель учета ряда факторов, введение третьего измерения приводят к значительному усложнению модели и резкому повышению размерности задачи. К тому же, в такой усложненной модели появляются параметры, которые невозможно или крайне трудно измерить. При их задании опять вводятся некоторые допущения, которые только затрудняют и ухудшают точность решения задачи.

Как показывает практика, использование детерминированных моделей с четкими значениями параметров (даже при наличии адаптационного процесса их уточнения путем решения обратных задач) приводит к тому, что модель оказывается излишне грубой. Методы интервального анализа дают возможность построить модель для случая, когда для каждого из этих коэффициентов задан интервал допустимых значений. Однако на практике в связи с наличием информации о том, что какие-то значения коэффициентов более допустимы, чем другие, описание этих коэффициентов в виде нечетких множеств является более удачным. В этом случае на интервале дополнительно задается функция принадлежности, причем, если информация о различии допустимости имеет статистический характер, то эта функция может быть определена объективно, если нет — то субъективно, на основе приближенного отражения экспертом в агрегированном виде имеющегося у него неформализованного представления о величине этого коэффициента.

Естественно, что введение нечетких коэффициентов усложняет процесс моделирования, однако в этом случае решение становится адекватным принятым упрощениям, например, при исключении третьей координаты z понятие в точке (х, у) становится размытым, нечетким, так как относится не к точке, а к интервалу.

В общем случае динамику дискретных систем можно представить уравнением состояния [166]:

,

,

где X - пространство состояний, U- множество допустимых управлений , F - переходная функция состояния, в общем случае нелинейная

.

Эта система является детерминированной, если в любой момент времени k можно однозначно определить ее новое состояние в момент времени (k+1) по текущему состоянию и управлению .

Для стохастических систем переходная функция записывается в виде

,

где XP - множество распределений вероятности на X. Для учета неопределенностей в модель могут вводится случайные величины или коэффициенты. Однако для этих моделей необходимо иметь информацию для построения вероятностных распределений.

Неполностью определенные процессы можно моделировать с помощью аппарата нечетких множеств. Коэффициенты и некоторые величины могут быть заданы в виде функций принадлежности. Тогда динамика системы описывается нечетким отношением

, (6.83)

представляющим собой нечеткое подмножество декартова произведения .

Величина рассматривается как интенсивность перехода или, точнее, как степень принадлежности элемента образу пары при отображении F, т.е. основной характеристикой системы является функция принадлежности .

Используя понятие нечеткого отношения, можно ввести следующие пути определения функции F:

1. Если отсутствует модель процесса и имеется лишь лингвистическое описание желаемого поведения системы вида "если давление газа очень большое, то значительно увеличить расход". Подобные выражения дают информацию о том, что должно произойти в системе при поступлении на ее вход управляющих воздействий в форме нечетких множеств, определенных на универсальных множествах "давление газа" и "расход". Тогда нечеткое условное высказывание есть нечеткое отношение, которое определяется как

;

; .

Если F будет являться нечеткой функцией, то состояние нечеткой системы в момент времени (k+1) есть условное по и нечеткое множество, характеризуемое функцией принадлежности .

2. Возможно использование имеющейся модели системы для задания функции F. Рассмотрим вначале случай свободной динамики системы и построим рекуррентную процедуру оценки состояния динамической системы в нечетких условиях.

В настоящее время для оценивания состояния динамических систем в теории оптимального оценивания широкое распространение получил байесовский подход. Однако достаточно приемлемые для практической реализации результаты получены лишь для случая линейных динамических систем с гауссовскими помехами. Для таких систем оценка состояния может быть проведена с использованием рекуррентного фильтра Калмана [67].

Рассматривались также методы, использующие фильтры Калмана для нелинейных относительно состояния систем и негауссовских помех [41]. При этом проводится предварительная линеаризация нелинейных уравнений объекта и канала наблюдений, а негауссовские помехи приближенно аппроксимируются гауссовскими, что приводит ухудшению точности результатов.

На практике ситуация также усложняется частичным или полным отсутствием информации о статистических характеристиках шумов. Поэтому авторами предлагается для решения задачи оценивания применять теорию нечетких множеств.

Рассмотрим нелинейную динамическую систему с дискретным временем:

, (6.84)

для которой измерение и состояние системы связаны соотношением:

. (6.85)

В этих уравнениях индекс kсоответствует k-му моменту времени;

- нелинейные функции соответствующих аргументов;

- состояние динамической системы,

- нечеткая помеха, заданная для каждого момента времени kфункцией принадлежности ;

- ошибка измерения с известной функцией принадлежности ;

Предполагается известной и функция принадлежности для начального состояния .

В процессе функционирования системы в общем случае носитель начального нечеткого состояния расширяется. Чтобы уменьшить неопределенность ситуаций при принятии решений, необходимо использовать дополнительную информацию о замерах и исследованиях в системе.

Будем предполагать независимость ошибок измерения, помех и состояния в смысле определения независимости нечетких величин. При заданной условной функции принадлежности состояния при наличии последовательности измерений наилучшая четкая оценка состояния в момент времени k может быть найдена из соотношения:

.

При наличии известной условной функции принадлежности оптимальная точечная оценка состояния системы в момент (k+1) может быть определена аналогично:

.

Поскольку для реальных процессов функции и являются унимодальными, то процедура нахождения максимума довольно проста. Для оценивания состояний выведем рекуррентную процедуру для функции принадлежности . На основании определения условной функции принадлежности можно записать, что

(6.86)

где вектор представлен в виде .

Используя определение (6.86) и уравнение для ошибки измерения получаем:

,

а из условия независимости , , следует, что

. (6.87)

Условную функцию принадлежности можно определить на основе уравнения динамики системы с использованием определения условной функции принадлежности:

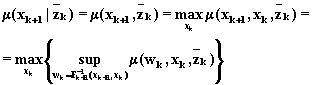(6.88)

Используя определение операции проектирования и учитывая соотношение (6.84), уравнение (6.88) может быть записано в виде

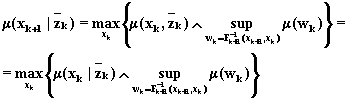
Используя в качестве характеристики нечеткого начального состояния априорную функцию принадлежности можно определить функцию , принимая во внимание (6.85):

. (6.89)

Окончательно рекуррентные соотношения для нахождения апостериорной функции принадлежности для нечеткого состояния системы на любом шаге (k+1) с учетом (6.89) можно записать:

; (6.90)

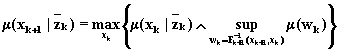. (6.91)

Для случая установившегося состояния используется только выражение (6.90), которое для этого случая принимает вид

. (6.92)

Если измерение отсутствует, то рекуррентная процедура сводится к соотношению

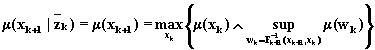. (6.93)

Рекуррентное соотношение имеет особенно простой вид в том случае, когда нечеткие шумы системы и ошибки измерения входят в (6.84), (6.85) линейно:

; (6.94)

. (6.95)

В этих уравнениях соответствия между и , и являются взаимно однозначными, поэтому для процедуры (6.90) выражение вида может быть представлено в следующей форме:

,

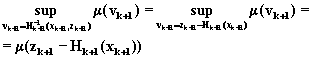а для уравнения (6.91) выражение вида можно преобразовать следующим образом:

.

Тогда рекуррентная процедура (6.90), (6.91) значительно упрощается и может быть представлена в виде:

; (6.96)

. (6.97)

Рекуррентные соотношения несложно реализуются практически, независимо от видов функций , и функций принадлежности , и .

В случае управляемой динамической системы также возможно использования имеющейся модели для задания функции F. Например, в случае линейной модели

, (6.98)

где на состояние и управление наложены нечеткие ограничения и задана нечеткая цель функционирования системы, для функций принадлежности с использованием определения образа нечеткого множества можно записать следующее соотношение:

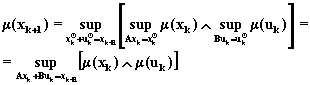(6.99)

В процессе функционирования системы в общем случае носитель начального нечеткого состояния расширяется. Чтобы уменьшить неопределенность ситуации при принятии решений необходимо использовать дополнительную информацию о проводимых замерах и исследованиях в системе.

Предполагается, что прямое измерение всего вектора текущего состояния системы невозможно, а процесс косвенного наблюдения описывается уравнением

,

где - нечеткий вектор замеров; H - функция измерений.

Для линейной модели (6.98) и линейного уравнения для замеров

можно записать следующую систему рекуррентных уравнений

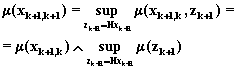; (6.100)

. (6.101)

В общем случае, когда функции F и H нелинейные, уравнения (6.100), (6.101) могут быть записаны в виде:

; (6.102)

. (6.103)

Рассмотрим теперь принципы управления нечеткой динамической системой для функции F вида (6.83). Допустим, что на управляющее воздействие в каждый момент времени kналожены нечеткие ограничения , характеризующиеся функцией принадлежности , и задано начальное состояние . Пусть - нечеткая цель, которую необходимо достигнуть в момент времени N. Эта цель характеризуется функцией принадлежности .

Оптимальные четкие управляющие воздействия могут быть определены следующим образом [54]:

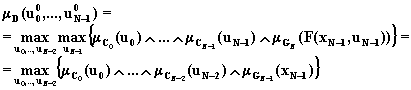(6.104)

где

(6.105)

Функция может рассматриваться как функция принадлежности для нечеткой цели в момент времени N-1, индуцированной конечной целью для момента N. Решение задачи может быть найдено с использованием метода динамического программирования следующей рекуррентной процедурой для промежуточной цели на момент N-j [54]:

(6.106)

где .

Таким образом, зная текущее нечеткое состояние , нечеткое ограничение и индуцированную нечеткую цель , на момент времени k можно найти эффективное четкое управление по (6.104), (6.105).

[К предыдущей главе].....[К содержанию] ......[К следующей главе]