В настоящее время только начинает создаваться комплексный подход к принятию решений в сложной многоуровневой иерархической системе газодобычи, которая учитывала бы иерархическую структуру управления, неопределенность измеряемых параметров и коэффициентов моделей, а также требования, накладываемые со стороны процесса разработки газового месторождения. Использование преимуществ иерархической структуры управления позволяет разделить алгоритм оптимизации на отдельные взаимосвязанные подзадачи, а применение теории нечетких множеств упрощает процедуру координации подзадач.
8.1. Детерминированные методы контроля и управления газодобывающими системами
Для рационального обоснования распределения ресурсов, выбора режимов работы технологического оборудования, проведения ремонтных работ и т.д. в газовой промышленности все шире начинают применяться количественные процедуры принятия решений. Однако в связи с наличием разнородной информации об объектах (детерминированной, качественной, статической, интервальной и т.д.), большими затратами времени и средств на измерения, необходимые для точной оценки параметров или вероятностных законов распределения, а также учитывая сложность многоуровневых иерархических систем, применение существующих детерминированных или вероятностных методов принятия решений является крайне затруднительным.
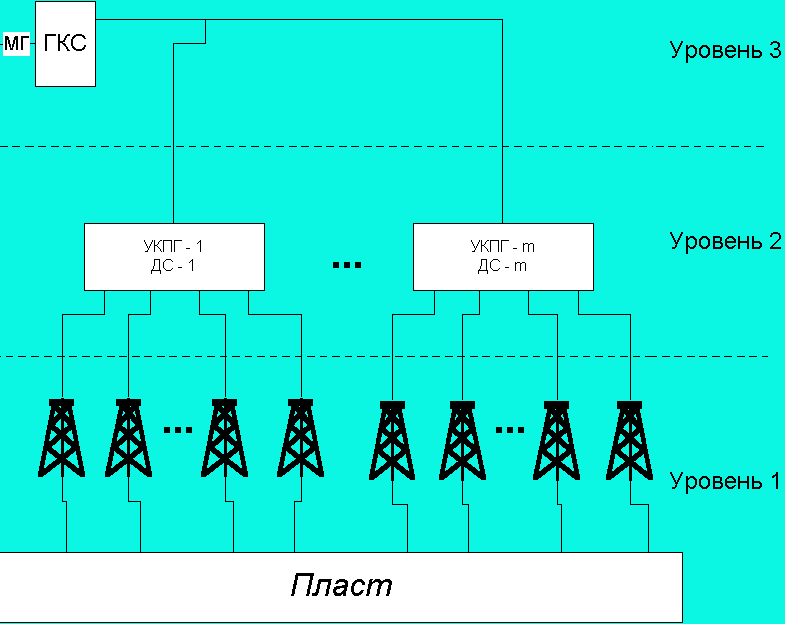
При освоении месторождений Тюменского региона создаются очень сложные и разветвленные системы сбора и межпромыслового транспорта газа (рис.8.1). Отличительными чертами таких систем являются: кустовое расположение скважин, разветвленная система шлейфов от скважин до УКПГ, сложная сетевая структура межпромыслового коллектора (МК), наличие нескольких (k) направлений магистрального транспорта газа (выходов системы) и головных компрессорных станций (ГКС).

Рис. 8.1. Структурная схема трехуровневой иерархической системы газодобычи
Промысловая информация характеризуется значительной степенью неопределенности, которая проявляется как в значительной погрешности измерений технологических параметров, так и в отсутствии замеров расходов, давлений и температур во многих узлах газотранспортной сети.
В настоящее время задачи по рациональному распределению отборов газа и выбора режимов работы технологического оборудования рассматриваются в основном лишь как одноуроневые одноцелевые. Это усложняет процесс согласования решений различных уровней, приводит к появлению определенных трудностей при использовании полученных результатов оптимизации на практике. На каждом уровне появляется также необходимость учета нескольких критериев, учитывающих эффективность работы технологического оборудования, минимальные затраты на подготовку газа, рациональность разработки газового месторождения и т.д. Многие цели противоречивы, и возникает необходимость принятия решения в конфликтной ситуации.
Расчетам гидравлических систем уделялось большое внимание в работах Х. Кросса, В.Г. Лобачева, М.М. Андрияшева, Б.Н. Пшеничного, М.Г. Сухарева, В.Я. Хасилева и других. Подробный обзор работ в этом направлении приведен в [153]. Все они развивают методы поконтурной и поузловой увязки для расчета транспротных сетей. Более сложные оптимизационные и расчетные задачи для гидравлических сетей поставлены и решены в работах А.П. Меренкова, В.Я.Хасилева [153]; А.Г. Евдокимова, А.Д. Тевяшева [92, 93, 94], М.Г. Сухарева, Е.Р. Ставровского [217, 218, 219], Р.Я. Бермана, В.С. Панкратова [60, 183], В.Б. Гармаша, В.В. Шершкова [11], Б.Н. Пшеничного [192], Б.Л. Кучина [137], П.Ф. Виллона [341], Д. Кралика [292, 293], М.А. Жидковой [97], И.В. Березиной, В.С. Ретинского [59], Е.И. Яковлева [55, 107], В.А. Юфина [55], Ю.И. Максимова [144], А.Ф. Воеводина, С.М. Шугрина [73], М.Н. Кулика [131], В.В. Дубровского [93].
Существует большое количество алгоритмов и программ расчета и оптимизации межпромысловых коллекторов [29, 30, 43, 44, 46, 47, 217, 126, 127, 134, 135, 147], газосборных сетей от скважин до УКПГ [43, 44, 46, 134, 154, 220, 221, 223, 153], режимов работы оборудования по очистке и осушке газа [43, 44, 46, 147, 220, 221]. Основные сложности применения этих моделей для диспетчерских и технологических расчетов связаны с невозможностью замера всех необходимых параметров в реальном масштабе времени с требуемой точностью во всех точках моделируемого технологического процесса. Очень часто при расчетах используются значения теоретических или паспортных коэффициентов моделей или производится итерационная процедура подбора этих коэффициентов диспетчером. Это иногда связано и с отсутствием замеров некоторых параметров, например, расходов газа. Наличие погрешности в замерах и коэффициентах моделей может привести к несовместности решений систем уравнений, а высокая размерность задачи затрудняет процесс поиска причин несовместности. Крайне сложной является проблема учета оптимальных решений, полученных при решении задач одного уровня управления, в решений задач другого уровня. В лучшем случае эти решения учитывались в виде интервальных ограничений, вводимых в задачу другого уровня.
Все это приводит к низкой точности получаемых результатов расчета и оптимизации, к сложностям при идентификации и повышенным требованиям к профессиональным знаниям пользователя и пониманию им всех тонкостей и ограничений математической модели.
Постановка
задачи: Имеется трехуровневая
система газодобычи которая
осуществляет сбор, подготовку и
межпромысловый транспорт газа.
Добыча газа производится из n
скважин, объединенных в m групп по ![]() скважин
в каждой j-ой группе. Каждая группа
скважин подает газ на свою УКПГ
через сложную систему шлейфов.
После подготовки газ поступает в
межпромысловый коллектор (МК) и
далее к k головным компрессорным
станциям (ГКС) магистральных
газопроводов (МГ).
скважин
в каждой j-ой группе. Каждая группа
скважин подает газ на свою УКПГ
через сложную систему шлейфов.
После подготовки газ поступает в
межпромысловый коллектор (МК) и
далее к k головным компрессорным
станциям (ГКС) магистральных
газопроводов (МГ).
На самом нижнем уровне иерархической системы моделей используются уравнения притока газа к забою и движения его по стволу скважины [134]:
![]() ; (8.1
)
; (8.1
)
![]() ; (8.2
)
; (8.2
)
где ![]() ; (8.3 )
; (8.3 )
![]() - пластовое, забойное
и устьевое давления i-ой скважины;
- пластовое, забойное
и устьевое давления i-ой скважины;
![]() - коэффициенты
фильтрационных сопротивлений;
- коэффициенты
фильтрационных сопротивлений;
![]() - коэффициент
сопротивления при движении газа по
стволу скважины;
- коэффициент
сопротивления при движении газа по
стволу скважины;
![]() - относительная
плотность газа по воздуху;
- относительная
плотность газа по воздуху;
![]() - глубина скважины;
- глубина скважины;
![]() - средняя абсолютная
температура газа в стволе скважины;
- средняя абсолютная
температура газа в стволе скважины;
![]() - средний коэффициент
сверхсжимаемости газа.
- средний коэффициент
сверхсжимаемости газа.
На дебиты скважин
накладываются ограничения в виде
нечетких множеств [35]: со стороны
процессов гидратообразования ![]() ,
разрушения прибойной зоны
,
разрушения прибойной зоны ![]() и
процессов обводнения конусом
подошвенных вод
и
процессов обводнения конусом
подошвенных вод ![]() .
.
Целевыми
функциями являются нечеткие
множества ![]() рациональных режимов работы
скважин по критерию равномерного
падения пластового давления и
равномерного стягивания контура
газоводяного контакта (ГВК).
рациональных режимов работы
скважин по критерию равномерного
падения пластового давления и
равномерного стягивания контура
газоводяного контакта (ГВК).
На втором уровне в качестве модели используются уравнения движения газа в шлейфах и регулирующих штуцерах [134]:
![]() ; (8.4
)
; (8.4
)
![]() ; (8.5
)
; (8.5
)
![]() ; (8.6)
; (8.6)
где ![]() -
давление газа в шлейфе после
штуцера и на входе j-ой УКПГ;
-
давление газа в шлейфе после
штуцера и на входе j-ой УКПГ;
![]() - коэффициенты
сопротивления при движении газа
через штуцер и в шлейфе;
- коэффициенты
сопротивления при движении газа
через штуцер и в шлейфе;
![]() - потери давления в
обвязках и на технологическом
оборудовании j-ой УКПГ.
- потери давления в
обвязках и на технологическом
оборудовании j-ой УКПГ.
На третьем уровне управления модель представляет собой систему уравнений стационарного движения газа по межпромысловому коллектору
![]() ; (8.7
)
; (8.7
)
![]() ; (8.8)
; (8.8)
где 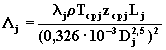 :
:
![]() - коэффициент
гидравлического сопротивления;
- коэффициент
гидравлического сопротивления;
![]() - длина линейного
участка (ЛУ);
- длина линейного
участка (ЛУ);
![]() - внутренний диаметр
трубы;
- внутренний диаметр
трубы;
![]() ,
, ![]() - множество
ребер, входящих в узел r и выходящих
из него.
- множество
ребер, входящих в узел r и выходящих
из него.
Газосборная сеть
задается в виде связного
ориентированного графа, имеющего N
узлов и L ребер. В соответствии с
процедурой декомпозиции эта
система уравнений может быть
дополнена для некоторых УКПГ
ограничением l (![]() ), учитывающим
зависимость давления на выходе
УКПГ от расхода газа
), учитывающим
зависимость давления на выходе
УКПГ от расхода газа
![]() , (8.9)
, (8.9)
где ![]() -
коэффициенты аппроксимации. Для
более сложных задач используются и
зависимости вида
-
коэффициенты аппроксимации. Для
более сложных задач используются и
зависимости вида ![]() . В качестве примера на
рис.8.2 приведена зависимость (8.9) для
УКПГ одного из северных
месторождений.
. В качестве примера на
рис.8.2 приведена зависимость (8.9) для
УКПГ одного из северных
месторождений.
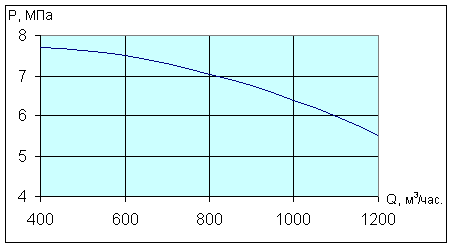
Рис.5.2. График выходного давления УКПГ
Технологические ограничения характеризуются максимальными и минимальными давлениями и расходами на входах в МК и выходах МГ
![]() ;
;
![]() ,
,
определяемые прочностью труб и производительностью ГКС. Кроме того заданы (m+k-J) граничных условий по давлениям и расходам, и температуры на входах МК.
Возможно проведение простого расчета режима или оптимизация режима работы газопровода по одному из следующих критериев:
1. максимум добычи
газа ![]() ;
;
2. максимум
давлений газа на входах в МГ ![]() ;
;
3. так распределить заданный отбор газа между УКПГ и скважинами, чтобы выбранный режим был эффективным с точки зрения разработки месторождения и работы технологического оборудования, допустимым технологически и не включал в себя режимов, имеющих высокую степень неопределенности.
Наиболее часто встречаются различные методы линеаризации, позволяющие свести систему нелинейных уравнений (8.7) - (8.9) к системе уравнений, линейных относительно квадратов давлений и расходов [293]
![]()
или ![]() , (8.10)
, (8.10)
где s - номер итерации.
На основе метода
линеаризации (8.10) система уравнений
(8.7) - (8.9) сводится к системе линейных
уравнений на шаге итерации s
относительно неизвестных расходов ![]() и
квадратов давлений
и
квадратов давлений ![]() ,
, ![]() . Размерность этой
системы может быть понижена путем
подстановки расходов из уравнений
(8.7) в уравнения (8.8). Полученная
система уравнений решается на
основе методов, разработанных для
симметричных систем с большим
числом нулевых элементов.
. Размерность этой
системы может быть понижена путем
подстановки расходов из уравнений
(8.7) в уравнения (8.8). Полученная
система уравнений решается на
основе методов, разработанных для
симметричных систем с большим
числом нулевых элементов.
Алгоритм
итерационного расчета состоит из
следующих этапов: с учетом
найденных начальных приближений
величин ![]() (некоторые способы их
нахождения обсуждены в [30]) решается
линеаризованная система уравнений
(8.7) - (8.9) для шага итерации s,
уточняются значения потоков по
каждому ребру, пересчитываются
коэффициенты
(некоторые способы их
нахождения обсуждены в [30]) решается
линеаризованная система уравнений
(8.7) - (8.9) для шага итерации s,
уточняются значения потоков по
каждому ребру, пересчитываются
коэффициенты ![]() и проверяется
критерий окончания счета -
обеспечение сбалансированности
потоков с заданной точностью x . Если
условие сбалансированности
выполняется, то расчет
заканчивается, в противном случае
итерационный процесс повторяется.
и проверяется
критерий окончания счета -
обеспечение сбалансированности
потоков с заданной точностью x . Если
условие сбалансированности
выполняется, то расчет
заканчивается, в противном случае
итерационный процесс повторяется.
Для расчета неизотермических процессов добавляется еще один итерационный цикл для пересчета температур газа в узлах сети [30]. Многочисленные примеры расчетов МК приведены в работах [29, 30, 134, 135]. При наличии на МК ДКС в систему уравнений добавляется уравнение для ДКС и расчет становится аналогичным расчету сетевого МГ.
8.2. Адаптивное оценивание нечетких коэффициентов уравнений
Перед расчетом
необходимо оценить вектор
коэффициентов ![]() в модели
в модели
![]() ,
(8.11)
,
(8.11)
где помеха ![]() вносит
некоторую неопределенность в
оценку
вносит
некоторую неопределенность в
оценку ![]() ; x –
вектор.
; x –
вектор.
Эта модель может
быть статической или динамической
(при включении в состав вектора x
прошлых значений y). Задача
оценивания может быть решена с
помощью различных методов:
наименьших квадратов,
максимального правдоподобия,
адаптации и т.д. При этом делаются
различные предположения о типе
помехи (аддитивная случайная
гауссовская с нулевым
матожиданием, мультипликативная и
т.д.), учитывается характер
априорной и апостериорной
информации о процессе и на основе
измеряемых величин ![]() , для
исследований проводится оценка
, для
исследований проводится оценка ![]() .
.
Рассмотрим два
метода оценивания на основе
нечеткого моделирования, которое
является одним из наиболее удачных
путей адекватного представления
наших объективных и субъективных
знаний об объекте. В этом случае
коэффициенты ![]() будем рассматривать
как нечеткие величины в своих
областях определения. Полученные
функции принадлежности для
будем рассматривать
как нечеткие величины в своих
областях определения. Полученные
функции принадлежности для ![]() могут
быть использованы в дальнейшем
непосредственно в нечетких моделях
типа (8.11), а также на их основе могут
быть получены точечные оценки.
Одним из путей построения
нечеткого множества L, которое
представляет коэффициент
могут
быть использованы в дальнейшем
непосредственно в нечетких моделях
типа (8.11), а также на их основе могут
быть получены точечные оценки.
Одним из путей построения
нечеткого множества L, которое
представляет коэффициент ![]() , может
служить следующий метод.
, может
служить следующий метод.
Пусть ![]() представляет собой вектор-столбец,
а положительно определенная
весовая матрица W, выбрана так, что
представляет собой вектор-столбец,
а положительно определенная
весовая матрица W, выбрана так, что ![]() представляет цену, связанную с
ошибкой
представляет цену, связанную с
ошибкой ![]() . Определим функцию С(а) как
. Определим функцию С(а) как
![]() (8.12)
(8.12)
Вектор нечетких
значений ![]() , при котором функция С(а)
достигает минимального значения,
обозначим
, при котором функция С(а)
достигает минимального значения,
обозначим ![]() . Тогда функцию
принадлежности любого
подмножеству L можно определить
следующим образом:
. Тогда функцию
принадлежности любого
подмножеству L можно определить
следующим образом:
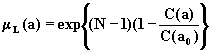 (8.13)
(8.13)
Используя
обобщенное понятие функции и
учитывая возможность наличия
нечетких ограничений С на
множестве Х, определяемых функцией
принадлежности ![]() , запишем функцию
принадлежности для нечеткого
множества решений А
, запишем функцию
принадлежности для нечеткого
множества решений А
![]() (8.14)
(8.14)
При необходимости
может быть найден вектор четких
решений ![]() , при котором функция
принадлежности
, при котором функция
принадлежности ![]() достигает своего
максимального значения.
достигает своего
максимального значения.
Для модели (8.11) может быть использована рекуррентная процедура оценивания коэффициентов a . Причем для удобства использования имеющейся на практике информации об ошибках замеров параметров в этом случае неопределенность в оценке a можно отнести за счет неточности замера входных xk и выходных yk параметров в момент времени k, т.е.
![]() ,
(8.15)
,
(8.15)
где zk, s k - точечные значения замеров входных и выходных параметров, n, w- нечеткие помехи с известными функциями принадлежности m (n) и m (w ).
Считается, что для
параметра a задана нечеткая
априорная характеристика m(a
). Предполагается,
что оцениваемый параметр a не
зависит от параметров входа и
выхода в смысле определения
независимости нечетких величин.
Тогда, используя понятие условной
функции принадлежности, при
наличии векторов замеров входного ![]() и
выходного
и
выходного ![]() параметров на момент
времени (k+1) имеем:
параметров на момент
времени (k+1) имеем:
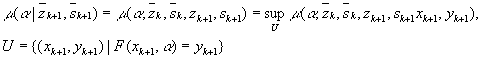
Используя далее условие независимости нечетких величин a , n , w можно записать:
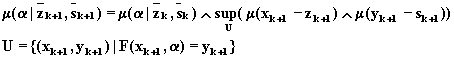 (8.16)
(8.16)
При наличии явной функциональной связи, выражение (8.16) можно упростить, исключив максимум по нечеткой величине y:
![]() (8.17)
(8.17)
Оптимальная оценка параметра a определяется следующим образом:
![]() (8.18)
(8.18)
Рассмотрим метод рекуррентного оценивания на примере оценки коэффициента гидравлического сопротивления l для уравнения стационарного движения газа по трубопроводу по замерам на момент времени k:
![]() (8.19)
(8.19)
где ![]() -
давление соответственно в начале и
конце линейного участка
трубопровода;
-
давление соответственно в начале и
конце линейного участка
трубопровода;
![]() - расход газа;
- расход газа;
с - константа.
Расход газа и давление измеряют с погрешностями
![]() ,
,
где для ошибок измерения n, wна основе характеристик измерительных приборов заданы функции принадлежности m (n ) и m( w ). Тогда, используя выражение (8.16), получаем
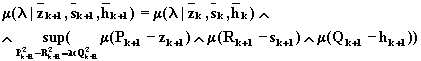 (8.20)
(8.20)
Функция принадлежности для отображения F: P* R* Q® lстроится численным методом по r-уровням нечетких множеств
![]() .
.
Процесс
адаптивного уменьшения
неопределенности и
соответствующего изменения
F-функции ![]() по мере поступления
оперативной информации для одного
из линейных участков
межпромыслового коллектора
Уренгойского месторождения
приведен на рис. 8.3. для нескольких
r-уровней.
по мере поступления
оперативной информации для одного
из линейных участков
межпромыслового коллектора
Уренгойского месторождения
приведен на рис. 8.3. для нескольких
r-уровней.
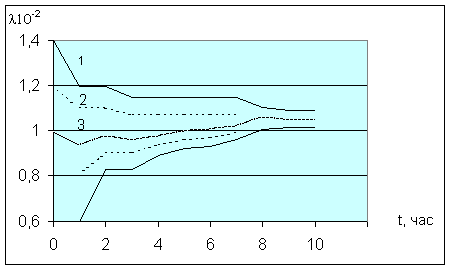
Рис.8.3. Изменение
функции принадлежности ![]() для
r-уровней 1- 0,1; 2 - 0,5; 3 - 1,0.
для
r-уровней 1- 0,1; 2 - 0,5; 3 - 1,0.
Для сравнения сходимости различных методов на рис.8.4. приведены результаты расчетов по классическому адаптационному алгоритму и максимизирующее решение алгоритма нечеткой адаптации.
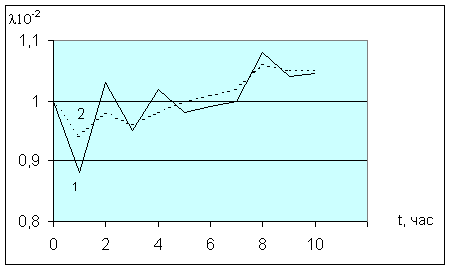
Рис.8.4. Графики
изменения ![]() при расчете по
классическому адаптационному
алгоритму (1) и максимизирующее
решение алгоритма нечеткой
адаптации (2).
при расчете по
классическому адаптационному
алгоритму (1) и максимизирующее
решение алгоритма нечеткой
адаптации (2).
[К предыдущей главе].....[К содержанию] ......[К следующей главе]