8.3. Идентификация фактических дебитов газовых скважин при неточных исходных данных и коэффициентах уравнений

В настоящее время на газовых промыслах севера Тюменской области дебиты отдельных скважин в оперативном режиме не замеряются. Замеры производятся лишь при проведении исследований скважин. Поэтому для систем газодобычи актуальна задача оценки дебитов газовых скважин при заданном давлении Р на входе УКПГ, ее производительности Q и по m замерам устьевых давлений на скважинах или, в случае их отсутствия, по пластовым давлениям . Очень высокая погрешность оценки дебитов скважин (20 - 30%) обусловлена в основном неточностью замеров расхода газа на УКПГ и устьевых (или пластовых) давлений и отсутствием точной информации о фактических коэффициентах гидравлических сопротивлений шлейфов, а если не замеряются устьевые давления - то и ввиду нечеткости оценки коэффициентов А и В и коэффициента гидравлического сопротивления по стволу скважин.

Существующие методы расчета фактических дебитов газовых скважин, например метод поправочных множителей, не учитывают этой имеющейся на практике неопределенности, что приводит к большим погрешностям расчета дебитов. Поэтому более правильным будет записать уравнение (8.4) стационарного движения газа по шлейфу как уравнение с нечеткими переменными.

Рассмотрим вначале случай, когда на скважинах поводятся оперативные замеры устьевого давления и каждая скважина подключена к УКПГ индивидуальным шлейфом. Для этого случая нечеткий дебит каждой скважины с учетом уравнения (8.1) запишется относительно нечетких величин следующим образом:

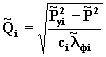(8.21)

Предположим, что нечеткость фактического коэффициента гидравлического сопротивления обусловлена неточностью нашего знания фактической эффективности Е, т.е.

, (8.22)

где для практических расчетов можно определить по формуле [56]

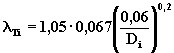(8.23)

Рассмотрим алгоритм расчета дебитов на примере, когда эффективность задана функцией принадлежности вида

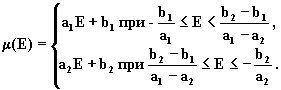(8.24)

1. Функция принадлежности для дебитов каждой i-ой скважины может быть найдена обратным аналитическим методом по r-уровням функций принадлежности нечетких параметров, для которых считаются справедливыми условия (8.2).

1.1. Воспользуемся выражением для r-уровня нечеткого множества , функция принадлежности которого была найдена в разделе 5 [39]:

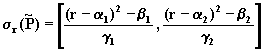(8.25)

1.2. Функция принадлежности для выражения находится по правилам возведения нечеткой величины в квадрат и деления на константу [68]:

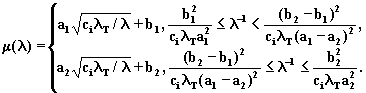(8.26)

Тогда соответствующий r-уровень функции определяется следующей формулой:

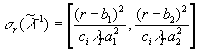(8.27)

1.3. Произвольный r-уровень функции принадлежности для допустимого дебита i-ой скважины находится с учетом выражений (8.25) и (8.27):

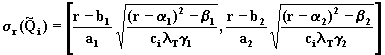(8.28)

2. Функция принадлежности допустимого расхода газа по УКПГ может быть вычислена для каждого дискретного r-уровня с учетом интервальных операций:

(8.29)

3. Скорректированную функцию принадлежности для суммарного расхода по УКПГ находим как пересечение полученной функции и функции , построенной по результатам замеров

(8.30)

4. Уточненные функции определяются последовательно с использованием численной процедуры, описанной в разделе 4 [39].

5. Точечные оценки искомых дебитов находятся по максимуму функций принадлежности :

(8.31)

После построения функций для дебитов скважин коэффициенты гидравлического сопротивления l и Е уточняются по алгоритму, описанному выше. При отсутствии замеров устьевых давлений алгоритм расчета фактических дебитов несколько усложняется. В этом случае необходимо учитывать уравнения притока газа к забою скважины ( находятся из решения задачи прогноза падения пластового давления на требуемый момент времени t)

; (8.32)

движения газа по стволу

(8.33)

и по шлейфу

(8.34)

Выражая дебит скважины из уравнений (8.32)-(8.34), получаем

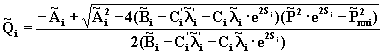(8.35)

Функция принадлежности находится обратным численным методом по дискретным r-уровням исходных функций [68]. Если принять, что коэффициент эффективности для всех шлейфов данной УКПГ является нечеткой величиной , то алгоритм оценки рабочих дебитов газовых скважин будет состоять из следующих этапов.

1. По замерам устьевых давлений и давления на входе УКПГ определяем нечеткую величину

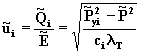(8.36)

2. Суммируем нечеткие величины :

(8.37)

3. Учитывая, что , получим выражение для совместной функции принадлежности

(8.38)

4. Далее, зная функцию принадлежности для нечеткой величины общего расхода (по результатам замера), оценим коэффициент эффективности

(8.39)

5. Тогда оценки фактических дебитов газовых скважин определяются следующим образом:

(8.40)

где

6. Точечные значения дебитов находятся из условия

(8.41)

В случае кустового подключения скважин нечеткие оценки рабочих дебитов определяются следующим образом:

1. По известным замерам общего расхода и давления на входе УКПГ рассчитывается нечеткая величина квадрата давления в точке врезки первой скважины

(8.42)

2. Оценивается дебит первой скважины

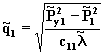(8.43)

3. Процедура вычислений является рекуррентной. Так, после некоторой точки врезки скважины i расход газа по основному шлейфу находится по уравнению

(8.44)

4. Вычисляется квадрат давления в точке врезки скважины (i + 1)

(8.45)

5. Оценивается дебит (i + 1) скважины

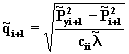(8.46)

Таблица 8.1.

Исходные данные для гипотетической УКПГ

* - Коэффициент сопротивления измеряется [(Мпа)²/(тыс.м/сут.)²]10^-6.

Таблица 8.2.

Результаты оценки дебитов (тыс.м³ /сут.)

По предложенной методике определялись фактические дебиты скважин для некоторых УКПГ Медвежьего и Уренгойского месторождений. В качестве примера в табл. 8.1 приведены исходные данные для гипотетической УКПГ (при входном давлении в УКПГ Р = 7,56 МПа и суммарном расходе Q = 11,075 млн.м ³/сут.). Результаты оценки дебитов для вышеупомянутых методов расчета рабочих дебитов газовых скважин сведены в табл. 8.2.

Допустимые интервалы для дебитов газовых скважин получены с учетом интервалов возможных значений коэффициентов гидравлических сопротивлений и погрешностей замеров давлений.

Величины вычислены по замерам давлений и теоретическому коэффициенту гидравлического сопротивления (Е=0,9). При этом млн.м³/сут. и значительно отличается от замера суммарного расхода на УКПГ.

Величины вычислены с помощью метода поправочного множителя . Этим достигается равенство .

Однако при этом некоторые дебиты скважин могут выйти за допустимый интервал. В предпоследней колонке табл. 8.2 приведены результаты вычислений по предложенной методике. В этом случае, оценки рабочих дебитов скважин получены с учетом погрешностей замеров давлений, суммарного расхода, неточности коэффициентов гидравлических сопротивлений и лежат в области допустимых значений .

8.4. Расчет и оптимизация режимов работы сетевого межпромыслового коллектора

Для крупных газовых месторождений Тюменского региона характерны сложные и разветвленные системы сбора и межпромыслового транспорта газа. Отличительными чертами таких систем является сложная сетевая структура межпромыслового коллектора, наличие нескольких направлений магистрального транспорта и установок комплексной подготовки газа. При вводе новых технологических объектов, изменении нагрузок установок комплексной подготовки газа, плановых заданий по добыче газа и при различных аварийных ситуациях возникает необходимость расчета различных режимов работы межпромыслового коллектора.

Стационарное движение газа при таком способе представления газосборной сети описывается системой нелинейных алгебраических уравнений (8.7) - (8.8).

Предположим теперь, что полученный граф имеет N узлов и L ребер. Понятие входящих и выходящих ребер определяет ориентацию графа. Поскольку каждое ребро графа характеризуется величиной расхода, а каждая вершина - величиной давления, то общее количество переменных равно N+L. Система (8.7), (8.8) имеет N-(K+M) уравнений типа (8.8) и L уравнений типа (8.7). Поэтому необходимым условием решения данной системы уравнений является задание K+M переменных.

Особенность рассматриваемого ниже итерационного метода решения состоит в том, что он позволяет производить расчеты для произвольных смешанных K+M переменных. При этом требуется выполнить следующие условия:

- если давление задается в узлах, то 1, поскольку в противном случае хотя бы одно из уравнений вида (8.8) можно представить линейной комбинацией остальных;

- для i-го ребра не должны быть одновременно определены так как уравнение (8.7) превращается в верное тождество;

- из тех же соображений нельзя задавать все , входящие в уравнение (8.8).

Алгоритм расчета состоит из следующих этапов.

1. Задается K+M переменных.

2. Начальное приближение величин определяется при решении методом последовательного исключения неизвестных линейной системы, составленной из уравнений вида

(8.47)

(8.48)

3. Решается система линейных уравнений относительно неизвестных расходов и квадратов давлений

(8.49)

(8.50)

где s - номер итерации.

4. Уточняются значения потоков газа по каждому ребру

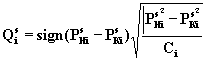(8.51)

5. Проверяется критерий окончания счета

(8.52)

где - заданная точность.

Если последнее условие выполняется, то расчет заканчивается. В противном случае необходимо вернуться к этапу 3.

Скорость сходимости алгоритма и время счета, естественно, тем меньше, чем меньше размерность системы. Можно свести систему (8.49), (8.50) к системе меньшей размерности, линейной относительно лишь квадратов давлений.

Пусть давление газа задается в узлах графа, следовательно, необходимо задать (K+M)- потоков газа. Все расходы, которые не заданы, находятся из уравнений (8.50)

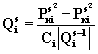(8.53)

В уравнениях (8.49) неизвестные величины расхода заменяются значениями правой части равенства (8.53). Таким образом, получают N-(K+M) линейных уравнений относительно N- неизвестных квадратов давлений. При добавлении к ним (K+M)- уравнений линейных участков (8.50), для которых потоки газа заданы, получают окончательную систему.

В отличие от традиционных методов расчета, в рассмотренном методе расчета стационарного движения газа по сложной сети газопроводов применяется итерационный метод, основанный на линеаризации уравнений (8.50) по расходам газа с их уточнением по формулам (8.51), что дает возможность уменьшить количество уравнений исходной системы с увеличением числа задаваемых давлений в узлах графа. Это позволяет значительно сократить время счета с одновременным уменьшением необходимого объема оперативной памяти.

Для газосборных коллекторов линейной структуры выход на режим с максимальной пропускной способностью не вызывает больших затруднений. Однако при наличии газосборного коллектора произвольной сетевой структуры это становится уже крайне сложной технологической задачей. Упрощение сетевого коллектора путем эквивалентирования, экспертные оценки технологов и диспетчеров дают слишком грубую ошибку по сравнению с фактическими данными. Поэтому пропускная способность такого коллектора в экстремальных ситуациях часто используется не полностью.

Задача определения максимальной пропускной способностиформализуется следующим образом. Входные технологические ограничения определяются допустимой производительностью установок комплексной подготовки газа:

(8.54)

(8.55)

Выходные ограничения определяются допустимыми режимами работы головных компрессорных станций:

(8.56)

Необходимо найти распределение по установкам комплексной подготовки газа входных расходов , максимизирующую целевую функцию

(8.57)

при системе ограничений (8.7)-(8.8), (8.54)-(8.56).

Метод расчетаоснован на линеаризации исходной системы уравнений по расходам газа и итерационном решении ряда задач линейного программирования.

1. Начальное приближение величин находится из максимизации суммарного расхода газа (8.57) с учетом линейной системы уравнений (8.47), (8.48) и ограничений (8.54)-(8.56). Эта задача относится к классу задач линейного программирования и может решаться симплекс-методом.

2. Для каждой следующей итерации s максимизируется целевая функция (8.57) с учетом линеаризованной по расходам системы уравнений (8.49), (8.50). Решение может также находится симплекс-методом.

3. По формуле (8.51) уточняются значения потоков газа по каждому ребру.

4. Проверяется критерий окончания счета (8.52).

Если последнее условие выполняется, то расчет заканчивается. В противном случае необходимо вернуться к этапу 2.

В штатных ситуациях обычно необходимо найти распределение заданного суммарного расхода по установкам комплексной подготовки газа

(8.58)

максимизирующее давление на входах головных компрессорных станций

(8.59)

при системе ограничений (8.7)-(8.8), (8.54)-(8.56) и (8.58).

Метод расчета также базируется на использовании линеаризации (8.50) и решении задачи линейного программирования на каждом шаге итерации. По сравнению с существующими способами решения подобных задач указанные методы обладают более быстрой сходимостью итерационного процесса (шесть - семь шагов) и значительно сокращают время счета.

[К предыдущей главе].....[К содержанию] ......[К следующей главе]