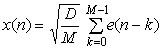1) с корреляционной функцией вида
Здесь D - дисперсия процесса, а а-определяет корреляцию (статистическую зависимость) соседних чисел (считаем а>0).
Для моделирования гауссовского случайного процесса с экспоненциальной функцией корреляции используется следующий алгоритм:
где e(n) - значения дискретного белого гауссовского шума с нулевым математическим ожиданием и единичной дисперсией. Параметрами модели в данном случае являются дисперсия выходного моделируемого процесса D и параметр а, который определяет статистическую связь соседних случайных отсчетов.
Как правило, на практике исходным параметром является нормированный коэффициент корреляции
| (3) |
который определяет нормированную корреляцию соседних отсчетов случайного процесса и практически задается из интервала от 0.9 до 0.9999. Когда этот коэффициент равен 1, то все значения случайного процесса становятся одинаковыми, а когда этот коэффициент стремится к 0, то получается рассмотренная ранее модель - дискретный белый гауссовский шум.
Программа 1 ( исходный файл lect2_1.cpp , выполняемый файл lect2_1.exe ).
На следующем фрагменте приведена программа моделирования реализации случайного процесса с экспоненциальной функцией корреляции:
#define N 500
#include "model.h"
#include <math.h>
float D = 1, a = 0.15;
float x[N];
void main(void)
{ float e, k1, k2; int n;
k2 = exp( - a );
k1 = sqrt( D*( 1. - k2* k2 ));
x[0] = gauss(0, D);
for(n =1; n <N; n++)
{ e = gauss(0, 1);
x[n] = k1* e + k2* x[n-1];
}
Init_graph();
graf_1("exp_korration ", x, 0, N-1);
Close_graph();
}
|
2) с корреляционной функцией вида
Здесь, как и раньше, D - дисперсия процесса, а а-определяет корреляцию (статистическую зависимость) соседних чисел.
Последовательность этапов моделирования следующая:
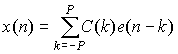 , , |
|
| где |
3) с корреляционной функцией вида
Здесь, как и раньше, D - дисперсия процесса, а а-определяет корреляцию (статистическую зависимость) соседних чисел.
Последовательность этапов моделирования следующая:
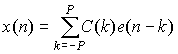 , , |
|
| где |
Таким образом, длительность реализации стационарного процесса с требуемой функцией корреляции равна N=N-2P.
4) с треугольной корреляционной функцией.
В рассматриваемом случае функция корреляции описывается формулой:
 .
.где ![]() , M определяет протяженность корреляционной функции, D - дисперсия случайного процесса. При других m R(m) = 0.
, M определяет протяженность корреляционной функции, D - дисперсия случайного процесса. При других m R(m) = 0.
Алгоритм моделирования реализации гауссовского случайного процесса с рассматриваемой корреляционной функцией заключается в следующем: