(2.25)2.4. Прямой аналитический метод нахождения результатов алгебраических операций
Для нахождения результатов алгебраических операций над F -величинами используются несколько аналитических и численных методов. Причем, если решение ищется для общего вида записи задачи (2.5), то метод называют “прямым”. Если метод основан на некоторой переформулировке исходной задачи с использованием a-уровней, то его называют “обратным” или методом a -уровневых сечений. Как и прежде, основное внимание будет уделяться операциям первого типа, которые определяются посредством (2.3).
Умножение F-величин на скаляр. Если B=l =( 1,l), то в силу взаимной однозначности отображения z= lx, из (2.3) получим
(2.25)
Если l=0, то очевидно, что
(2.26)
т.е. если A - нормальная F-величина, то 
.
Сложение F-величины со скаляром. Аналогично предыдущему случаю, если B=l =(1, l), и, следовательно, z=x+ l, то
(2.27)
Этим самым
осуществляется сдвиг функции 
вправо
или влево по вещественной оси на
величину |l|.
Нетрудно проверить, что соотношения (2.25)-(2.27) справедливы и для алгебраических операций второго типа.
Пример 2.11. Пусть A=( 1-(x-1)2, (0,1)) . Тогда, согласно (2.25) и (2.26) имеем
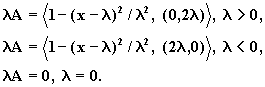
Из (2.27) получим
В разделе 2.2 было
отмечено, что нахождение F-величины 
, т.е.
нахождение ее F-функции, сводится к
решению параметрической
экстремальной задачи (2.5). Причем, с
помощью замены из уравнения связи 
данная
задача преобразуется в задачу без
ограничений (2.7), т.е. для операций
первого типа получим
.
(2.28)
Из теории экстремальных задач [41, 71, 163, 233] хорошо известно, что нахождение глобального максимума некоторой функции на заданном множестве U из R существенно упрощается, если эта функция унимодальна, т.е. имеет на U единственный максимум.
Нетрудно
заметить, что если F-величина А строго
выпукла и функция достигает на 
своей
верхней грани, то унимодальна на 
. Если А-
выпуклая, то это уже не так. Тем не
менее, даже для выпуклой F-величины нахождение
верхней грани ее F-функции значительно
проще, чем для F-величины с
произвольной F -функцией.
Следовательно,
предпочтительнее решать задачу (2.28)
для выпуклых F-величин, поскольку
функция 
определяет выпуклую F-величину. Исключение
составляет операция умножения,
когда множества и 
содержат нуль в
качестве внутренней точки. Кроме
того, для выпуклых F-величин справедливо
следующее утверждение.
Теорема 2.7.Если
Aи B - выпуклые, то 
-
выпуклая F-величина.
Доказательство.
Рассмотрим операцию сложения.
Пусть 
, 
, 
и 
, 
. Тогда для
произвольного 
имеем
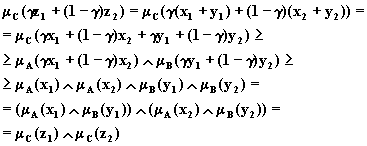
что и требовалось доказать.
Поскольку 
, а (-В)-
выпуклая F-величина,
то для операции вычитания
утверждение теоремы можно считать
тоже доказанным.
Рассмотрим
операцию умножения, т.е. 
. Пусть 
, 
, 
и 
, 
.
Положим для определенности, что 
, 
, 
. Тогда для
произвольного 
найдутся 
и 
с
условием 
. Пусть 
, для которых
,
,
.
Тогда получим
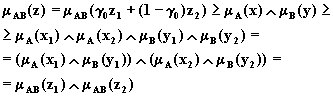
что и требовалось доказать.
Для операции
деления утверждение доказывается
аналогично, причем, если 
, то 
. Таким
образом теорема доказана
полностью.
Предположение о
выпуклости F-величин
обусловлено также тем, что
большинство функций
принадлежности на практике
являются выпуклыми. В некоторых
случаях может оказаться полезным
следующий подход к решению задачи
(2.5), который можно назвать принципом
декомпозиции. Если возникает
ситуация, когда A и B - невыпуклые, то их
можно представить в виде
объединения выпуклых F -величин. Из
определения алгебраических
операций над F-величинами нетрудно
заметить, что если 
, то
(2.29)
Следовательно, если А и В - невыпуклые, то представление их в виде объединения выпуклых F-величин в некоторых случаях может облегчить решение задачи (2.5). Имея ввиду все отмеченные выше обстоятельства, в дальнейшем будем предполагать, что все используемые F-величины являются выпуклыми.
В основе прямого
аналитического метода для бинарных
операций лежит классический подход
к поиску точек экстремума функции
на некотором множестве из R. Будем предполагать,
что функция 
всегда достигает своей
верхней грани на s
(A) кроме тех
случаев, когда верхняя грань
достигается в точках -
или + .
Тогда, как известно [41], точками экстремума
функции (x) наs(A) могут быть лишь те
точки, в которых выполняется одно
из следующих условий:
1. либо (x) терпит разрыв;
2. либо (x) непрерывна, но
производная 
не существует;
3. либо существует
и равна нулю;
4. либо x=a или x=b, если s(A)=[a, b].
Если множество s(A) неограниченно,
то нужно также изучить поведение
функции (x) при
x ® - или +.
Рассмотрим теперь каждую из операций над F -величинами.
Сложение F-величин. В этом случае уравнение связи имеет вид x+y=z
т.е. для
произвольного фиксированного z
0 величина
равна
верхней грани функции
для (2.3)
на прямой в R2 с уравнением y= z0-x. Соотношение (2.28)
запишется в виде
(2.30)
Из (2.30) видно, что
значениями функции 
являются
верхние грани семейства F-величин 
,
зависящих от z как
от параметра. Если в зависимости от z
экстремальные
точки функции 
можно выразить в виде
соотношений:
x=j 1(z), x=j2 (z), ..., x=j n(z),
то получим
где
.
Следует отметить
то обстоятельство, что точка
глобального максимума функции 
в
некоторых случаях может быть
получена непосредственно из
решения уравнения
.
Проиллюстрируем выше изложенное рядом простых примеров.
Пример 2.12.
Пусть 
, 
.
Тогда из уравнения 
имеем 
, откуда 
,
, и,
следовательно, 
, 
.
Делая соответствующие подстановки, после несложных преобразований получим
,
. (2.31)
Поскольку 
, то 
, т.е. 
.
Пример 2.13.
Пусть 
и 
.
Тогда из уравнения
получаем 
Делая
подстановку 
, находим
Таким образом,
Пример 2.14. Если
и
, то по аналогии с
предыдущим примером из анализа
уравнения
получим, что
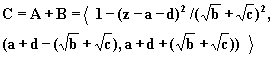(2.32)
Пример 2.15.
Пусть 
и 
, где
,
, 
,
,
В общем случае
графики функций 
и 
показаны на рис.2.6.
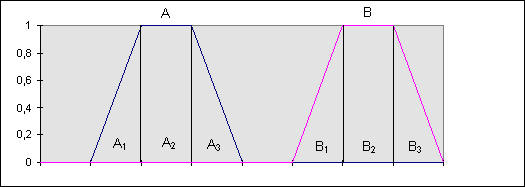
Рис.2.6.
Графики функций 
и 
.
В данном случае можно воспользоваться принципом декомпозиции, причем соответствующий анализ показывает, что
.
(2.33)
Из уравнения 
находим,
что 
и, следовательно,
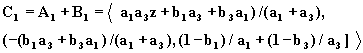(2.34)
По аналогии для 
имеем
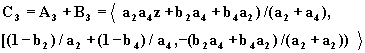(2.35)
И, наконец,
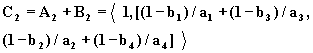(2.36)
Пример 2.16. Пусть 
и 
. Тогда из уравнения
получим
,
.
Таким образом,
x1 = j 1(z) = -z,
x2 = j2(z) = z/3.
Делая соответствующие подстановки,
получаем
В этом случае
Приведем один пример на сложение второго типа, определяемого по (2.4).
Пример 2.17. Пусть A и B из примера 2.12. Тогда из уравнения
получим, что
и, следовательно,
.
(2.37)
Вычитание F-величин. В этом случае уравнение связи имеет вид
z = x - y,
т.е. для
произвольного фиксированного z0
величина
равна
верхней грани функции
на
прямой в R2 с уравнением y= z0-x. Соотношение (2.28)
запишется в виде
.
(2.38)
Кроме того, поскольку A-B=A+(-B), т.е. вычитание сводится к сложению, то эта задача не представляет самостоятельного интереса. Поэтому ограничимся двумя примерами.
Пример 2.18. Пусть A и B из примера 2.13. Тогда из уравнения
получаем
Делая подстановку
,
находим
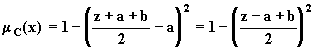
Таким образом,
Пример 2.19. Пусть A и B из примера 2.12. Тогда из уравнения
имеем 
, откуда 
,
, и,
следовательно,
,
(2.39).
Окончательно,
.
По аналогии с примером 2.17 нетрудно показать, что для вычитания второго типа
.
(2.40)
Умножение F-величин. В этом случае уравнении связи имеет вид
z = x y,
т.е. для
произвольного фиксированного z0
величина 
равна
верхней грани функции
на
гиперболе в R2 с уравнением y=z0
/x. Соотношение
(2.28) запишется в виде
(2.41)
Ввиду нелинейности ограничения нахождение произведения F-величин представляет собой более трудную задачу, чем суммирование и вычитание.
Пример 2.20. Пусть A и B из примера 2.16. Тогда из уравнения
получаем
.
.
Делая
соответствующую подстановку 
,
получаем
Пример 2.21. Пусть
A и B из примера 2.12. Из
уравнения 
получим 
,
. Из первого
уравнения имеем 
, откуда
.
Следовательно, 
, 
,
где 
.
Осталось
рассмотреть еще одно уравнение 
, из которого
.
Обозначая 
, получим 
,
.
Учитывая, что 
и,
рассматривая арифметические
значения корней, окончательно
имеем:
,
(2.42)
.
(2.43)
Рассмотрим
частный случай данного примера.
Пусть 
,
т.е. 
.
Тогда для 
получим
, 
Поскольку при 
имеем
то окончательно
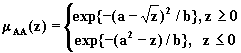
Если 
, то 
,
.
Таким образом, 
, т.е.
результат не зависит от положения
точки а . При
а=0 получаем
Интересно
отметить, что если отображение 
трактовать как возведение F-величины А в
квадрат, то при а=0 получим
,
т.е. в этом смысле 
.
Очевидно, что это справедливо для
любой F -величины,
носитель которой содержит нуль в
качестве внутренней точки.
Пример 2.22. Пусть
A и B из примера 2.15. Для
упрощения рассмотрим частный
случай, когда 
, т.е. 
. Здесь также можно
использовать принцип декомпозиции.
Соответствующий анализ показывает,
что
.
(2.44)
Очевидно, что 
.
Соотношение 
приводит
к уравнению 
, из
которого следует
.
Учитывая, что 
, получим
.
Из уравнений 
и 
следует
.
Аналогично, на основе уравнения
с учетом ограничений на коэффициенты, получим
,
откуда
.
Например, если 
, т.е. 
, то
получим
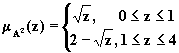
Графики F-функций 
и 
показаны
на рис 2.7.
Рис. 2.7.
Графики F-функций
и 
.
Деление F-величин. Уравнение связи в этом случае имеет вид
z = x / y, y
0,
т.е. для
произвольного фиксированного
z0 величина
равна
верхней грани функции
на
прямой в R 2 с уравнением х=z
0у.
Следовательно, можно записать
.
(2.45)
Вообще говоря, операция деления F-величины А на B сводится к умножению A на 1/B. С другой стороны, ввиду линейности ограничения x=zy операция деления во многих случаях значительно проще операции умножения.
Пример2.23. Пусть 
и 
. Тогда из уравнения
получаем
y1 = j 1(z) = 2/(z-1),
y 2 = j2 (z) = 6/(z+1).
Делая соответствующие подстановки, получаем
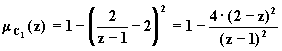
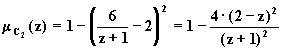
Таким образом,
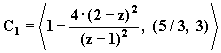
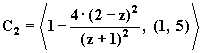
В этом случае 
.
Пример 2.24. Пусть А и В из примера 2.14. Из уравнения
получаем
,
,
т.е.
,
,
Учитывая условие 
,
рассмотрим следующие случаи.
1. Числа a и d одного знака, т.е. 
. Анализ
функции 
в зависимости от знака
величин 
показывает, что
,
для которых
,
(2.46)
,
(2.47)
где берутся
арифметические значения
квадратных корней из c и b. Поскольку при 
, а при 
, то
получаем
(2.48)
Следствие.
Очевидно, что если нуль не является
внутренней точкой для 
, то 
.
Следовательно, из (2.48) имеем 
.
2. Числа a и d разных знаков, т.е. 
. Анализ
функции 
показывает, что
,
для которых
,
.
Поскольку при 
, а при 
, то
получаем
(2.49)
Следствие.
Очевидно, что если нуль не является
внутренней точкой для 
, то 
, т.е. 
.
Следовательно, в этом случае 
.
Пусть, например, 
, т.е. 
и
являются ограниченными, т.е.
множества 
и 
- ограниченные. Тогда из (2.46)
получим, что
,
график которой показан на рис. 2.8.
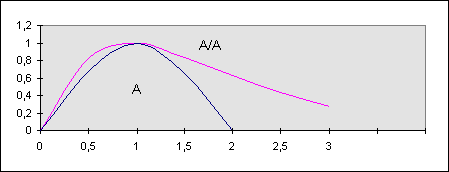
Рис. 2.8.
Графики F-функций
и 
.
Таким образом, 
-
неограниченное множество. Это
является следствием того, что нуль
является граничной точкой для 
.
Пусть 
, т.е. 
, 
. В этом случае 
,
т.е. является ограниченной.
Пусть 
.
Поскольку 
, то из (2.46) и (2.47) получаем
,
.
Окончательно
, 
.
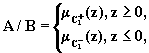
Пример 2. 25. Пусть 
, 
, 
. Пользуясь результатами предыдущего
примера, получаем.
1. Если 
, то
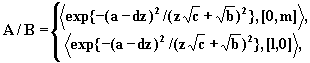
где 
,
.
Следствие.
Если 
или
, то
,
где 
, если 
и
, если 
.
1. Если 
, то
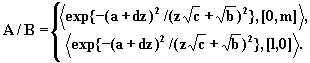
Следствие.
Если 
,
то 
и,
следовательно,
,
где 
, если 
и
, если 
.
Пример 2.26. Пусть A и B из примера 2.22. В этом случае
.
(2.50)
Введем следующие обозначения:
,
.
Из уравнения
получим
и, следовательно,
.
(2.51)
Аналогично получаем
.
(2.52)
И, наконец,
.
(2.53)
Пусть, например, 
. В этом
случае
,
,
.
F -функция 
показана
на рис.2.9.
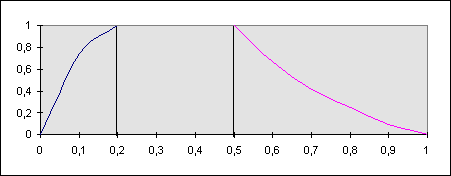
Рис. 2.9.
График F-функции
.
На примерах данного параграфа можно убедится, что нахождение результатов алгебраических операций второго типа связано, как правило, с гораздо большими техническими трудностями.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]