2.5. Обратный аналитический метод нахождения результатов алгебраических операций
В предыдущем
разделе задача нахождения функции ![]() ,
задаваемой соотношением
,
задаваемой соотношением
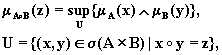 (2.54)
(2.54)
решалась так
называемым прямым методом, т.е. для
произвольного ![]() определялось
определялось ![]() .
.
В основе обратного метода нахождения результатов алгебраических операций лежит важное следствие из следующей теоремы.
Теорема 2.8.
Пусть X и Y - произвольные базовые
множества, A![]() F(X) и
задано отображение f: X® Y. Если для "y
F(X) и
задано отображение f: X® Y. Если для "y![]() Y $x
Y $x![]() X такой, что
X такой, что ![]() , то
справедливо равенство
, то
справедливо равенство
![]() (2.55)
(2.55)
Доказательство.
Пусть ![]() такое,
что
такое,
что ![]() .
Тогда
.
Тогда ![]() ,
т.е.
,
т.е. ![]() и,
следовательно,
и,
следовательно, ![]() .
.
С другой стороны,
пусть ![]() , т.е.
, т.е. ![]() .
Тогда по условию теоремы
существует
.
Тогда по условию теоремы
существует ![]() такой, что
такой, что ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() . Теорема
доказана.
. Теорема
доказана.
Следствие.
Если A, B![]() F(R) , то
F(R) , то
![]()
Доказательство.Как
было отмечено ранее,
алгебраические операции
определяются отображением f:R* R®R , т.е. для F-величин A и B имеем f(A* B)=A°B. Учитывая, что в данном
случае справедливо равенство ![]() , с
учетом (2.55) получаем
, с
учетом (2.55) получаем
![]()
что и требовалось доказать.
Очевидно, что указанная теорема и следствие справедливы также для слабых a -уровневых множеств.
F-величина A называется ограниченной
, если s(A) - ограниченное
множество. Подкласс из F(R) ограниченных и
выпуклых F-величин
обозначим через ![]() .
.
Из условия теоремы следует, что доказанное следствие выполняется, когда основное соотношение (2.54) можно записать в виде
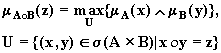 (2.56)
(2.56)
Суть обратного
метода решения задачи (2.56) для
ограниченных и выпуклых F -величин заключается в
следующем. Если A, B![]()
![]() , то для произвольного a из[0,1], пользуясь указанным
следствием, можно найти a-уровневое
множество для A°
B. Этим самым
определяется элемент
, то для произвольного a из[0,1], пользуясь указанным
следствием, можно найти a-уровневое
множество для A°
B. Этим самым
определяется элемент
![]()
из класса ![]() ,
находящегося во взаимно
однозначном соответствии с
,
находящегося во взаимно
однозначном соответствии с ![]() (теорема
1.3).
(теорема
1.3).
Разрешая
уравнения ![]() относительно a , получим образ
элемента
относительно a , получим образ
элемента ![]() в классе
в классе ![]() относительно биекции T:
относительно биекции T:
![]() ®
®![]() , т.е. F- функцию
, т.е. F- функцию ![]() . Таким
образом, название данного метода
вполне согласуется с идеей,
положенной в его основу.
. Таким
образом, название данного метода
вполне согласуется с идеей,
положенной в его основу.
Заметим, что
обратный метод согласно теореме 2.8, можно применять для
нахождения F-величины
f(A) при
отображении f: R®R,
A![]() F(R) . Поскольку
F(R) . Поскольку ![]() , то
следствие теоремы можно записать
так
, то
следствие теоремы можно записать
так
![]() , (2.57)
, (2.57)
где символ · обозначает интервальную алгебраическую операцию [247].
Приведем несколько примеров нахождения результатов алгебраических операций над F-величинами обратным методом.
Пример 2.27
.Пусть А и В
из примера 2.12, т.е. ![]() . Найдем F-величину A+B. Имеем
. Найдем F-величину A+B. Имеем
![]()
откуда
![]()
следовательно,
![]()
![]()
Далее
![]()
![]()
откуда
![]()
т.е. для всех z имеем
![]() ,
,
что совпадает с результатом (2.31), полученным прямым методом.
Пример 2.28.
Пусть А и В
из примера 2.12, т.е.
![]() и
и ![]() . Тогда
из уравнений
. Тогда
из уравнений
![]() ,
,
![]()
получим
![]()
![]()
Как и в предыдущем примере из соотношений
![]()
![]()
следует
![]() ,
,
![]() ,
,
что совпадает с результатом (2.32).
Пример 2.29 . Для А и В из примера 2.15 имеем
![]() ,
,
![]() ,
,
откуда
![]() ,
,
![]() .
.
Из соотношения
![]()
получаем
![]()
при ![]() .
.
Аналогично, из равенства
![]()
получаем
![]()
при ![]() .
.
Кроме того, ![]() , если
, если
![]()
Полученный ответ совпадает с результатом примера 2.15.
Пример 2.30. Рассмотрим операцию вычитания для A и B из примера 2.13. Тогда из уравнений
![]() ,
, ![]()
получим
![]()
![]()
Далее из соотношений
![]()
![]()
следует, что для всех z имеем
![]()
т.е.
![]()
что совпадает с результатом примера 2.13, полученным прямым методом.
Пример 2.31. Рассмотрим операцию умножения для A и B из примера 2.20. В этом случае имеем
![]() ,
, ![]()
откуда
![]()
![]()
В нашем случае
![]() .
.
Таким образом, для всех z>0 имеем
![]() ,
,
т.е.
![]() ,
,
что совпадает с результатом примера 2.20, полученным прямым методом.
Пример 2.32. Рассмотрим еще
операцию умножения для A и B из примера 2.28 при
условии, что ![]() . В этом случае имеем
. В этом случае имеем
![]() ,
,
откуда, обозначая ![]() , получим
уравнение
, получим
уравнение
![]() ,
,
решения которого имеют вид
![]() .
.
Следовательно,
![]() .
.
Учитывая условие ![]() ,
получаем
,
получаем
![]() .
.
Очевидно, что решение уравнения
![]()
дает тот же результат.
Пример 2.33. Рассмотрим операцию деления для A и B из примера 2.23. Из уравнений
![]() ,
, ![]()
имеем
![]()
В этом случае
![]()
Для решения достаточно одного уравнения. Следовательно,
![]() ,
,
откуда
![]() ,
,
т.е.
![]() .
.
При a=4 и b=2
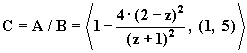 ,
,
что совпадает с результатом примера 2.23, полученным прямым методом.
Пример 2.34. Для A и B из примера 2.32 найдем F- величину A/B. В этом случае
![]() ,
, ![]()
Для решения достаточно одного уравнения. Следовательно, имеем
![]() ,
,
откуда
![]() ,
,
т.е.
![]() .
.
Этот же результат был получен прямым методом в примере 2.24 (3-е следствие).
Алгебраические операции второго типа. Обратный метод решения задачи
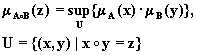
заключается в следующем. Уравнение
![]()
описывает линию
уровня функции ![]() в плоскости (х,у).
Пусть
в плоскости (х,у).
Пусть ![]() -
выпуклая F-величина,
т.е. для любой точки (х,у) из
области, ограниченной линией
уровня, выполняется неравенство
-
выпуклая F-величина,
т.е. для любой точки (х,у) из
области, ограниченной линией
уровня, выполняется неравенство
![]() .
.
Тогда очевидно, что если кривая, описываемая уравнением
![]() .
.
Касается границы данной области, то
![]() . (2.58)
. (2.58)
Следовательно,
если установлена функциональная
зависимость ![]() , в которой z и t
удовлетворяют (2.58), то
, в которой z и t
удовлетворяют (2.58), то
![]() .
.
Пример 2.35 . Пусть A и B из примера 2.12 найдем F-величину A+B. Уравнение линии уровня в этом случае имеет вид
![]() , (2.59)
, (2.59)
а уравнение связи
![]() ,
,
которое описывает
линию уровня функции ![]() при
некотором фиксированном
при
некотором фиксированном ![]() . В данном
случае существуют две точки
касания:
. В данном
случае существуют две точки
касания: ![]() и
и ![]() . Поскольку вектор-градиент
. Поскольку вектор-градиент
![]()
в любой точке на
прямой ![]() и,
кроме того, в
и,
кроме того, в ![]() имеет одно направление с
имеет одно направление с ![]() , а в
, а в ![]() -
противоположные, то тангенс угла
наклона вектора-градиента
-
противоположные, то тангенс угла
наклона вектора-градиента ![]() в точках
касания равен единице. Поскольку
в точках
касания равен единице. Поскольку
![]() ,
,
то, следовательно,
![]() ,
,
где ![]() -
некоторая точка касания. С учетом
(2.59) имеем
-
некоторая точка касания. С учетом
(2.59) имеем
![]() ,
,
![]() .
.
Подставляя ![]() (или
(или ![]() ) в
уравнение связи, получаем
) в
уравнение связи, получаем
![]() ,
,
откуда
![]() .
.
Этот же результат был получен прямым методом в примере 2.17.
Рассмотренные
аналитические методы построения
функции принадлежности ![]() позволяют
получить результат операции сразу
в аналитическом виде, что очень
удобно для практических
приложений. Однако на практике
могут встречаться более сложные
аналитические выражения для
исходных F-величин,
для которых имеются значительные
трудности при нахождении
аналитического решения. К тому же,
иногда возникает необходимость в
численных методах работы с
дискретно заданными F-функциями. В этом
случае F
-величинаA°B также будет
дискретной. Для практических
приложений этого, как правило,
вполне достаточно. При
необходимости полученное решение
можно аппроксимировать некоторой
функциональной зависимостью.
позволяют
получить результат операции сразу
в аналитическом виде, что очень
удобно для практических
приложений. Однако на практике
могут встречаться более сложные
аналитические выражения для
исходных F-величин,
для которых имеются значительные
трудности при нахождении
аналитического решения. К тому же,
иногда возникает необходимость в
численных методах работы с
дискретно заданными F-функциями. В этом
случае F
-величинаA°B также будет
дискретной. Для практических
приложений этого, как правило,
вполне достаточно. При
необходимости полученное решение
можно аппроксимировать некоторой
функциональной зависимостью.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]