3.1. Анализ интервальных методов

При управлении различными технологическими процессами необходимо обеспечить в реальном масштабе времени расчет и оптимизацию режима, который гарантированно будет лежать в области допустимых режимов и будет реализуем системами автоматического управления нижнего уровня иерархической системы управления. Стандартно применяемые методы мало подходят для решения задач такого класса ввиду низких скоростей сходимости вещественных итерационных методов типа метода Ньютона и возможности появления произвольных неконтролируемых ошибок в результатах при наличии погрешностей в исходных данных. Кроме того, в зависимости от имеющегося вида неопределенности при принятии решений необходимо обеспечить проведение на ЭВМ расчетов с интервальными и нечеткими величинами.

Например, особенности управления системами газоснабжения заключаются в том, что даже редкие колебания давлений и расходов сверх определенных пределов (прежде всего прочностных) могут привести к авариям. Поэтому при управлении такими системами приходится ориентироваться на самое неблагоприятное (экстремальное) сочетание факторов неопределенности и использовать понятие гарантированного результата [116, 137].

Наиболее перспективными для нахождения решений систем уравнений с учетом отмеченных особенностей работы алгоритмов реального времени в условиях неопределенности являются интервальные [109, 175, 277, 304, 323] и нечеткие [2, 166] методы. Эти методы получили большое распространение при решении систем дифференциальных уравнений [109, 247, 304], систем линейных и нелинейных уравнений [109, 175, 232, 234], задач глобальной оптимизации [323].

Применение интервального анализа и различных минимаксных (гарантированных) подходов [48, 49, 116, 133, 242, 304] обладает целым рядом преимуществ:

- не требуется знание вероятностных характеристик неопределенных факторов, которые редко бывают точно известны на практике;

- при минимаксном подходе получают строгие оценки для самих искомых величин, а не для вероятностей или математических ожиданий, что имеет большое значение при наличии малого числа замеров параметров и одной или нескольких реализаций;

- cтатистические характеристики не могут гарантировать определенный исход одного конкретного опыта;

- во всех случаях даются гарантированные двусторонние аппроксимации искомых решений.

При минимаксном подходе операции над неопределенными величинами сводятся к соответствующим операциям над областями, однако даже в случае простых исходных областей неопределенности в результате операций над ними получаются области сложной формы, требующие для своего описания большого числа параметров [242]. Поэтому на практике применяется аппроксимация области неопределенности классом областей, зависящим от фиксированного числа параметров: параллелепипедами [247], эллипсоидами [50, 242] и т.д. Ставятся и задачи минимизации объема результирующих областей неопределенности [242].

В общем случае точность интервального результата полностью определяется следующими четырьмя факторами [8]:

1. Неопределенностью в задании исходных данных.

2. Округлениями при выполнении операций, изменяющих или порождающих интервальные объекты.

3. Приближенным характером используемого численного метода.

4. Степенью учета зависимостей между участвующими в вычислении интервальными объектами (переменными и константами).

Увеличение точности расчетов (уменьшение ширины результирующего интервала) достигается за счет компенсации влияния этих факторов. Задача получения для данного множества машинно-представимых чисел самого узкого интервала, содержащего объединенное расширение соответствующей рациональной функции, может ставиться как оптимизационная.

Для уменьшения погрешности округления используются изменение разрядности чисел, различные способы машинного представления и специальное упорядочение цепочки следующих друг за другом операций. А компенсация влияния четвертого фактора осуществляется путем предварительной обработки исходного алгоритма, в процессе вычислений и апостериорно [8].

Как отмечается в Добавлении А.Г.Яковлева к [8] широкое распространение интервальной арифметики обусловлено фактическим отсутствием конкурентноспособных подходов к построению надежного (в смысле гарантированности) и транспортабельности (по включению) программного продукта для решения численных задач. Интервальный подход позволяет навести математическую строгость в построении численных алгоритмов, которые традиционно основывались на аппроксимации точного значения одним "достаточно близким" к нему приближением. Для интервальных методов даются гарантированные двусторонние аппроксимации искомых решений [48], имеющие смысл наихудшего случая с точки зрения описания неопределенностей [249].

В связи с важностью понятий интервального анализа для теории нечетких множеств приведем основные понятия и методы из [109].

3.1.1. Интервальная арифметика

Интервальные числа

Пусть – множество всех вещественных чисел. Под интервалом , всюду ниже, если не оговорено противное, понимается замкнутое ограниченное подмножество вида

.

Множество всех интервалов обозначим через . Элементы будем записывать прописными буквами. Если А – элемент , , то его левый и правый концы будем обозначать как . Элементы называются интервальными числами.

Символы и т. п. понимаются в обычном теоретико-множественном смысле, причем обозначает не обязательно строгое включение, то есть соотношение допускает равенство интервалов. Два интервала А и В равнытогда и только тогда, когда .

Отношение порядка на множестве определяется следующим образом: А< В тогда и только тогда, когда . Возможно так же упорядочение по включению: А не превосходит В, если . Мы, в основном, используем первое определение.

Пересечениеинтервалов А и В пусто, если А < В или В< А, в противном случае – снова интервал.

Симметричным, по определению, является интервал , у которого .

Шириной интервала А называется величина . (3.1)

Серединаесть полусумма концов интервала А: . (3.2)

Абсолютная величинаопределяется как . (3.3)

Наконец, . Нетрудно заметить, что , когда , причем , если и .

Расстояниемежду элементами вводится равенством

.

Вырожденный интервал, то есть интервал с совпадающими концами , отождествим с вещественным числом а. Таким образом, .

Стандартная интервальная арифметика

Арифметические операции над интервальными числами определяются следующим образом. Пусть , . Тогда , (3.4)

причем в случае деления .

Легко проверить, что определение (3.4) эквивалентно соотношениям

, (3.5)

, (3.6)

, (3.7)

. (3.8)

Заметим, что операцию вычитания можно выразить через сложение и умножение, положив и .

В зависимости от знака чисел правило (3.7) для интервального умножения будет выглядеть так (мы полагаем ):

1.

2.

3.

4.

5.

6.

7.

8.

9.

Отсюда видно, что только в одном (последнем) случае для нахождения произведения требуется четыре умножения, а в остальных достаточно двух умножений.

Если А и В – вырожденные интервалы, то равенства (3.5)–(3.8) совпадают с обычными арифметическими операциями над вещественными числами. Таким образом, интервальное число есть обобщение вещественного числа, а интервальная арифметика – обобщение вещественной.

Из определения (3.4) непосредственно видно, что интервальные сложение и умножение ассоциативны и коммутативны, иначе говоря, для имеют место равенства

Роль нуля и единицы играют обычные 0 и 1, которые, как отмечалось, отождествляются с вырожденными интервалами и . Другими словами,

для любого . В дальнейшем точку для обозначения умножения будем, как правило, опускать.

Равенство (3.4) (как и (3.5)–(3.8)) показывает, что если один из операндов является невырожденным интервалом, то результат арифметической операции также невырожденный интервал. Исключение составляет умножение на . Отсюда, в частности, следует, что для невырожденного интервала А не существует обратных по сложению и умножению элементов, так как если А + В = 0, АС = 1, то А, В, С должны быть в силу сказанного вырожденными. Короче, вычитание не обратно сложению, деление не обратно умножению. Значит, , когда . Понятно, однако, что всегда .

Субдистрибутивность

Интересным свойством интервально–арифметических операций является невыполнение закона дистрибутивности – равенство

А(В + С) = АВ + АС(3.9)

не всегда имеет место. Действительно, , в то время как . Однако всегда справедливо включение

, (3.10)

называемое субдистрибутивностью. В самом деле, если , то это значит, что , где . Но , следовательно, .

Отметим некоторые важные случаи, когда (3.10) совпадает с (3.9). Будем называть интервал А нуль содержащим интервалом(н.с.-интервалом), если . Положим, по определению,

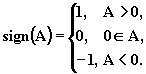(3.11)

Пусть в каждом из произведений А(В+С), АВ, АС нет одновременно двух н.с.-интервальных множителей. Тогда имеет место цепочка равенств

(3.12)

Полученное выражение будет нулем или в случае , или же когда . Для выполнения последнего равенства необходимо и достаточно, чтобы не только bc, но и были положительными. Это будет так, если либо или , либо . Сказанное справедливо для А, не являющегося н.с.-интервалом. Для н.с.-интервала А приведенные выводы остаются верными, когда ни один из интервалов В, С, В + С не будет н.с.-интервалом. Если А и В + С – н.с.-интервалы, а ни В, ни С таковыми не являются, первое в цепочке равенств (3.12) заменяется строгим неравенством, и, таким образом, (3.9) не имеет места. Ничего определенного нельзя сказать в случае, когда А, В + С и В и (или) С – н.с.-интервалы. Однако для симметричных интервалов В и С дистрибутивность (3.9) всегда имеет место.

Итак, установлено, что:

1. всегда справедливо (3.10);

2. если или , или , то А(В + С) = АВ + АС ;

3. если А – не н.с.-интервал, то А(В + С) = АВ + АСтогда и только тогда, когда ;

4. если , где , то А(В + С) = АВ + АС ;

5. если В и С– симметричные, то А(В + С) = АВ + АС.

Монотонность по включению

Интервальная арифметика обладает таким важным свойством, как монотонность по включению. Это значит, что если , то

(3.13)

(если ).

Эти соотношения прямо вытекают из определения (3.4). Пользуясь тем, что отношение включения транзитивно, мы приходим к следующему фундаментальному результату.

Теорема 3.1.

Если является рациональным выражением от интервальных переменных , то есть конечной комбинацией интервалов и конечного набора постоянных интервалов, соединенных интервальными арифметическими операциями, то из , следует

при любом наборе интервальных чисел , для которого интервальные арифметические операции в выражении имеют смысл (то есть не встретится деление на интервал содержащий нуль).

Эту теорему иногда называют основной теоремой интервальной арифметики.

3.1.2. Обобщения интервальной арифметики

Интервальная арифметика с нестандартными вычитанием и делением

Нестандартные операции вычитания и деления , определенные для элементов , вводятся следующим образом [109]:

,

Обозначим и укажем некоторые свойства, связанные с операциями и .

1. .

2. , , для (по определению ).

3. Из равенства не следует ; например,

.

4. Для уравнение имеет единственное решение: .

5. Для уравнение имеет решение . В случае у этого уравнения есть еще одно решение: .

6. Уравнение имеет решение . Если , то существует еще одно решение: .

7. тогда и только тогда, когда или , или .

8. .

9. , , для (по определению ).

10. Из равенства не следует ; например,

.

Определим для элементов функцию следующим образом:

.

11. Уравнение при имеет решение тогда и только тогда, когда , которое выражается в виде .

12. Уравнение при имеет решение . Если , то существует еще одно решение: .

13. Уравнение имеет решение . Если , то имеется еще одно решение: .

14. тогда и только тогда, когда или , или .

Ряд других свойств интервальной арифметики с нестандартными вычитанием и делением можно найти в [109].

Обобщенная интервальная арифметика

Некоторые присущие интервальной арифметике свойства, такие как A-A 0, A /A 1, и т.п., в ряде случаев приводят к возрастанию ширины получаемых в результате вычислений интервалов. Обобщенная интервальная арифметика позволяет во многих случаях уменьшить влияние этих отрицательных свойств обычной интервальной арифметики. Будем представлять интервал X = [ x, x ] в виде x = y + [ -c, c ], где y = m (x), c = v (x) 0 . Таким образом произвольная точка x X записывается в виде x = y + x , x [ -c, c].

Допустим нам требуется найти интервал, содержащий множество значений рационального выражения, зависящего от n переменных, изменяющегося в исходных интервалах X ₁, … , X _n .

Представим каждую переменную x _iX_i в виде

x_i = y_i + x_i, x_i [ -c _i, c _i ]

Любой интервал

` X_i = Y_i + a_(r=1..n)x_rZ _ir , (3.14)

где Y_i , Z_ir , i=1,..,n некоторые интервалы, а x_r[ -c _r, c _r ].

Интервал` X_i записанный в виде (3.14), называется обобщенным интервалом.

Полагая Y_{i =} [y_i, y_i ], Z _ii = [1,1], Z _ir = [0,0], r i , x_r [ -c _r, c_r ], имеем `X_i= X_i

Определим арифметические операции на обобщенными интервалами.

Пусть X_i = Y_i + a_(r=1..n)x _r Z _ir , X_j= Y_j + a_(r=1..n)x_r Z _jr

Положим X_{i *} X_j = Y_k+ a_(r=1..n)x_r Z _kr, где * { +, -, · , / }

Для каждой из этих операций в отдельности правила вычисления интервалов Y_k, Z_kr следующие:

сложение Y_k = Y _i + Y _j

Z_kr = Z_ir + Z_jr, r=(1..n)

вычитание Y_k = Y_i - Y_j

Z_kr = Z_ir - Z _jr, r=(1..n)

умножение Y_k = Y_i Y_j + a_(r=1..n) [0, c²_r] Z_irZ_jr,

Z_kr = Y_i Z_jr + Y_jZ_ir+ Z_ir a_{(s=1,sr, по n)}[-c_s, c_s] Z_is = Y_i Z_jr + Y_j Z_ir + [-1,1] ·| Z_ir | · a _{(s=1,s r, по n)} c_s|Z_is|

деление Y_k = Y_i / Y _j

Z_kr = (Y_j Z _ir - Y_i Z_jr) / Y_j (Y_j + [-1,1] a_{(s=1, по n)}c_s|Z_is| )

Нетрудно показать, что если

x_iX_i= Y_i + a_(r=1..n)x_r Z _ir ,

x_j X_j= Y_j + a_(r=1..n) x_r Z _ir , (3.15)

то x_i* x _jX_i*X_{j , *}{ +, -, · , / }.

Пример 3.1.Вычислим множество значений функций

f(x)=x-x и g(x₁, x₂) = x ₁ - x ₂,

x₁, x₂[0,1]. В первом случае полагаем

x = + x , x [ -, ],

а во втором случае

x₁ = + x₁, x ₂ = + x ₂, x₁,x₂ [ -, ],

Y ₁ = Ѕ, Y₂ = Ѕ, Z₁₁= Z₂₂ = 1, Z ₁₂ = Z₂₁ = 0,

что после сведения к интервалам дает

f([0,1]) = 0 + [ - , ] ·0 = 0

g([0,1], [0,1]) = 0 + [ - , ] · 1 + [ - , ] ·1 = [-1, 1]

Во введенном Каханом обобщении интервальных операций допускается деление на интервал, содержащий 0, и наличие ситуации, когда для интервала [8].

Обобщенная интервальная арифметика может применятся для сужения интервалов, содержащих множества значений функции в некоторых случаях. Однако при широких исходных интервалах (на которых задана функция) она зачастую дает интервалы шире чем другие способы. При очень узких или вырожденных интервалах лучше использовать обычную интервальную арифметику, т.к. обобщенная требует больше арифметических операций, а значит машинного времени.

[К предыдущей главе].....[К содержанию] ......[К следующей главе]