3.1.3. Интервальные функции

Включение областей значений функций вещественных пeременных в интервальные полиномы

Применение интервальных расширений в вычислительных процессах позволяет находить интервалы, гарантированно содержащие решения (множество решений) тех или иных задач. Заметим, что для этих целей часто достаточно наличия такой интервальнозначной функции , что и, в частности, , и не требуется обязательного выполнения равенства . Будем называть монотонную по включению интервальнозначную функцию F(X₁,…,X_n) n интервальных переменных RB-расширением функции, если f(X₁,…,X_n)ОF(X₁,…,X_n) для всех X=(X₁,…,X_n) из области задания f. На практике в качестве RB-расширения чаще всего используются интервальные полиномы. Рассмотрим ряд примеров.

Пример 3.2. Пусть функция f(x) определена и ограничена при xОX(0) : u f (x) v. Тогда постоянная интервальная функция F(X)=[u,v] будет RB-расширением для f(x).

Пример 3.3. Если f(x) - аналитическая при x ОX^* функция, R_p (X) - монотонное по включению интервальное расширение p-го коэффициента ряда Тейлора функции f(x), то интервальный полином

(3.16)

будет RB-расширением для f(x) и имеем f(x)ОF_p(x) МF_p(X) для всех xОXМX^*.

Пример 3.4. В двух конкретных случаях - для функций e^x и sin x - формула (3.16) выглядит так:

f(x)=e^x, X*=[0,1], x*=0:

f(x)=sin x, x*=0: sin x Оx-x³/3!+...+((-1)^p-1/(2p-1)!)x^2p-1 +[-1,1]x^2p+1/(2p+1)!

Интервальные расширения функций в виде MV-формы

Ввиду того что w (F(X)) - w ((X))=O(w (X)) , разность весьма быстро стремиться к нулю при w (X)® 0. К сожалению, центрированная форма не всегда монотонна по включению. Это можно видеть на примере функции f(x)=x(1-x). Центрированная форма первого порядка F(X) имеет вид

F(X)=f( c ) + (1 - 2c)(X - c) - (X - c) .

Для X = [0, 1], X= [0, 0.9], XI X , однако F(X) = [0, 0.2925], F(X) = [0, 0.25],т.е. F(X) F(X). Во многих интервальных методах существенно используется свойство монотонности по включению, необходимое для получения гарантированных границ искомых решений. Рассмотрим другой способ построения интервальных расширений, основанный на применении теоремы о среднем значении (mean value theorem - отсюда название MV-форма), впервые использованный Р. Муром. Заметим сразу, что он применим для гораздо более широкого класса функций, а не только для рациональных и распространяется на обширный класс операторов, например на интегральные.

Пусть f : R® R - непрерывно дифференцируемая функция, XО I(R) - интервальный вектор, c = m(X) . Для любого yО X имеет место равенство

f ( y ) = f ( c ) + (x )( y - c), x ОX.

Если - интервальное расширение функции ¶f/¶ x = f на X, то

f ( y ) Оf ( c ) + (X)( X - c). (3.17)

Значит, выражение, стоящее в правой части соотношения (3.17), определяет интервальную функцию, являющуюся интервальным расширением функции f на X. Эта функция называется MV-формойинтервального расширения функции f или просто MV-формой.

Будем обозначать ее как F(X) :

F(X) = f (m(X) ) + (X)( X - m(X)). (3.18)

Покажем, что MV-форма монотонна по включению.

Лемма. Для любых трех интервалов P, Q, T О I( R ), Q T и любого вещественного p О P справедливо включение

p(m(Q) - m(T))+P(Q - m(Q)) P(T - m(T)).

Доказательство. Учитывая симметричность интервала

Q - m(Q) = w(Q)[-1/2, 1/2],

имеем

p(m(Q) - m(T))+P(Q - m(Q))= p(m(Q) - m(T)) + | P| w(Q)[-1/2, 1/2].

Так как Q T , то

|p(m(Q) - m(T))| |P| |m(Q) - m(T)| | P| (w(T) - w(Q))/2.

Из этого неравенства получаем

p(m(Q) - m(T)) + |P| w (Q)[-1/2, 1/2] | P|(w (T) - w(Q))[-1/2, 1/2] + | P| w (Q)[-1/2, 1/2]=

= |P| w(T)[-1/2, 1/2]=P(T _ m(T)),

что и требовалось доказать.

Теорема 3.2.Если функции , j=, монотонны по включению, то и MV-форма F также монотонна по включению.

Доказательство. Пусть X , X ОI(R), X X, с = m(X ), i= . Тогда

= + , x О X.

Поскольку монотонны по включению, то

.

Теперь утверждение теоремы вытекает из леммы, если в ней положить P=( X), p=, Q=X , R=X.

Методы сужения интервалов. Метод Скелбоу

Прямое применение способа Мура получение границ, сколь угодно близких к f(x₁, x₂, ...x_n) требует большого количества вычислений интервальных расширений (того или иного вида) функции к f(x₁, x₂, ... x_n). Сколбоу предположил метод, позволяющий существенно сократить объем вычислений. В качестве интервального расширения используется центрированная форма дающая наименьшую нижнюю границу для f. Области различной величины, используемые в вычислениях, упорядочиваются в виде списка так, что нижние границы , вычисленные на этих областях, возрастают. Если дальнейшее подразбиение конкретной области дает новые нижние границы, превосходящие нижние границы на каких-то других областях из списка, то только тогда эти области далее подразбиваются, на них вычисляется и список переупорядочивается. Процедура продолжается до тех пор, пока разность между двумя последовательными нижними границами не станет меньше заданной величины.

Поясним сказанное на примере функции одной переменной. При р=8 возможна следующая ситуация (рис.3.1).

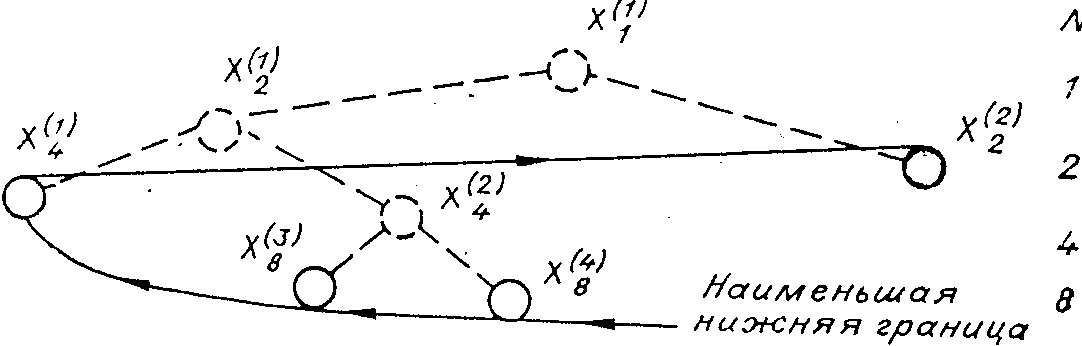
Рис 3.1.

В обозначениях имеем . Следующий шаг включает разбиение и вычисление соответствующих значений интервальной функции. Эти значения вносятся в список в нужном порядке,a , которое теперь не нужно, отбрасывается. Предположим, что . Это дает возможности:

1) тогда продолжаем процесс при р=32;

2) .

Во втором случае необходимо разбить , вычислить соответствующие значения функции, а результаты упорядочить. Действия по этой схеме продолжаются до тех пор, пока не получится наименьшая нижняя граница, соответствующая р=16. Итерации прекращаются тогда, когда разность между двумя последовательными нижними границами и , не станет меньше , e— заданное число.

Для получения верхней границы процесс повторяется с -¦ вместо ¦. Данный метод можно использовать не обязательно с рациональными ¦ , только в этом случае вместо центрированной формы надо взять какой-либо другой тип интервального расширения, например MV-форму.

Применение обобщенной интервальной арифметики

Получение границ для `f(X) с помощью обобщенной интервальной арифметики проиллюстрируем на нескольких простых примерах .

Пример 3.5. Рассмотрим функцию f(x₁,x₂ )=(x₁+x₂)/(x ₁+x₂), X₁=[l, 2], X₂=[5, 10]. Интервалы Х₁и X₂, представим в виде X₁=3/2+x₁, x₁=[-1/2, 1/2], X₁ =15/2+x₂, x₂=[-5/2, 5/2]. Положим Х₃= Х₁+X₂ , X₄=Х₁-X₂. Тогда`f(Х₁,X₂) Х ₅=X₃/Х₄. Учитывая правила арифметических действий над обобщенными интервалами, будем последовательно иметь Х₃= 9 +x₁+ x₂, X₄= -6 +x₁-x ₂ и, наконец, Х ₅= -9/6 +x₁[-5/6, -5/18]+ x₂[1/18, 1/6]. После сведения к интервалам, т. е. заменяя x₁ на [1/2, -1/2], x₂ - на [-5/2, 5/2], найдем X₅ = [-7/3, -2/3] I [-2.334, -0.6666]. Тот же результат получил Мур с помощью центрированной формы. MV-форма в этом случае приводит к более широкому интервалу [-67/18, 13/18]. Прямое вычисление Х₁ +X₂ в обычной интервальной арифметике дает интервал [-4, -2/3]. Точное множество значений

` f (Х₁, X₂) = l+2/( Х₁/ X ₂ -l) = l+2/([l/10, 2/5]-1) = 1 + 2/[-9/10, -6/10] =

= 1 + [-20/6, -20/9] = [-7/3, -11/9] [-2.334, -1.222].

Пример 3.6. Возьмем f(x)=-(1+x+x² )/(1+x+2x²), x О X= [-0.001, 0.003].

Вычисляя (1+X+Х²)/(1+Х+2Х²) с помощью обычной интервальной арифметики (с точностью до (6знаков), получим интервал [0.995994, 1.00402]. Обобщенная интервальная арифметика дает [0.999991, 1.0001]+ x [-0.00200503, -0.00198498], и после сведения к интервалу [0.999986, 1.00001] объединенное расширенно

f(` X)О[0.999991, 0.999999]. Таким образом, результат, полученный с помощью обобщенной интервальной арифметики, заметно точнее результата применения обычной интервальной арифметики.

Обобщенная интервальная арифметика может быть полезна при решении многих задач. Заметим, однако, что при широких исходных интервалах она зачастую дает интервалы шире, чем, к примеру, центрированная форма. При очень узких или вырожденных интервалах, по-видимому, лучше использовать обычную интервальную арифметику, поскольку обобщенная требует больше арифметических действий, а значит, машинного времени.

Вычисления с помощью нестандартной арифметики

Арифметикой с нестандартными операциями можно эффективно пользоваться для вычисления объединенных pacширений функции, удовлетворяющих определенным условиям монотонности.

ПустьD О (I_i), функция f(x) определена при xО D. Обозначим через М(D) множество всех монотонных на D функций. Если fО M(D), то объединенное расширение`f(X), легко вычисляется:

`.

Будем говорить, что (f, g) О M(D) удовлетворяют условию монотонности M₁ , если функции f, g одновременно обе возрастают или обе убывают. Пара f, g удовлетворяет условию M₁,если одна из функций f , g возрастает, а другая — убывает. Будем, по определению, полагать А A В = A - (-В), A, BОI (R).

Теорема 3.3. Если f, g таковы, что h = f + g ОМ (D), то при всех XО D

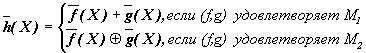
Если f, g таковы, что h = f - g О M(D),то

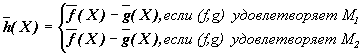
Если f и g таковы, что | f| , | g| , h = f· g О M(D), то

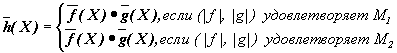
Здесь А B = A : (1/B). Если f и g таковы, что | f}| , | g| О M(D), g(x) 0, xОD и h = f/g О M(D), то для любого X О D

`

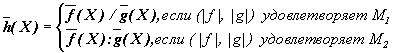
Доказательство утверждении теоремы легко получается с использованием монотонности фигурирующих в ней функций. Рассмотрим примеры ее применения.

Пример 3.7.Вычислить ` h(Х), где h(x)=x² + x, xОR. Объединенным расширением функции f(x)=x является

` f(X)=X. Если 0 является не принадлежит Х, то для g(x)=x <sup>2</sup>, ` g(X)=X·X=X ². Функция h(x)=x+x² монотонна на всяком интервале Х таком, что —1/2 не принадлежит X. Таким образом, объединенное расширение` h(X) монист быть вычислено с помощью теоремы 1 для любого X, не содержащего точек -1/2 и 0, и мы имеем

`

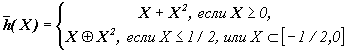
Пример 3.8. Для h(x) = x - x ²применение теоремы 3.3 дает

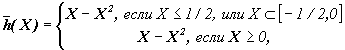
Пример 3.9. Для функции е^x ={е^{x |}хОХ} при Х0 можно записать

e^x = 1 + X/1! + Х²/2! + . . .

Рассмотрим Х 0. Ряд Тейлора для e^x запишем в следующем виде:

е^x = х + 1 + x³/3! + x² /2! + x⁵/5! + x⁴/4! + x⁷/7! + ...

Все частичные суммы этого ряда монотонно возрастают при хО (-, 0]. Применяя теорему 3.3, получим для Х 0

Если.

3.1.4. Интервальные векторы и матрицы

Пусть Rⁿ - множество всех n-мерных векторов a=(a₁,a₂,...,a_n), a_i О R, i=. Через I(Rⁿ) обозначим множество всех n-мерных интервальных векторов, т. е. множество упорядоченных интервалов A=(A₁,A₂,...,A_n), A_i О I(Rⁿ), i=. Аналогично и I() есть соответственно множество всех вещественных и интервальных матриц размера . Так же как и интервальные числа, будем обозначать интервальные векторы и матрицы прописными буквами.

Если aО Rⁿ (соответственно ), AО I(Rⁿ) (соответственно I()), то запись aО A, означает a_i ОA_i, i=(соответственноa_ij О A_ij,i=, j=). Точно так же для элементов I(Rⁿ), I() соотношение A B понимается в смысле покомпонентного включения.

Будем считать, что пересечение для интервальных векторов пусто, если хотя бы для одного i. В противном случае .

Для A=(A₁,A₂,...,A_n), по определению, полагаем

, (3.19)

m(A)=(m(A ₁), ..., m(A_n)).(3.20)

Далее, норма интервального вектора A есть

, (3.21)

а расстояние между векторами A и B

. (3.22)

Для AI I() будем обозначать через m(A) матрицу с элементами m(A_ij), i,j=, , а в качестве нормы используем

. (3.23)

Легко видеть, что если A, BО I(Rⁿ) или I(), то из AB вытекает,.

Если aО R ⁿ, то операторы Pr_i определяются равенствами Pr_ia=a _i, i=.

Система линейных алгебраических уравнений с интервальными коэффициентами

Рассмотрим систему линейных алгебраических уравнений вида

(3.24)

где SО I(), FО I(Rⁿ). Уравнение (3.24) понимается в следующем смысле: требуется найти множество

, s О S, fО F}.

Обозначим еще , i=. Множество решений может иметь весьма замысловатую структуру. Например, Хансен показал, что при

,

изображается на плоскости (u₁, u₂) в виде невыпуклого восьмиугольника (рис.3.2).

Понятно, что нахождение и точное описание таких множеств в случае n, больших двух, чрезвычайно затруднительно и вряд ли целесообразно.

В рамках интервального исчисления можно поставить задачу нахождения интервального вектора U=(U₁,U₂,...,U_n) такого, что , i=. Оптимальным интервальным решением назовем такой интервальный вектор, компоненты которого удовлетворяют условиям

, i=,

где inf и sup берутся по всем возможным решениям , i=.

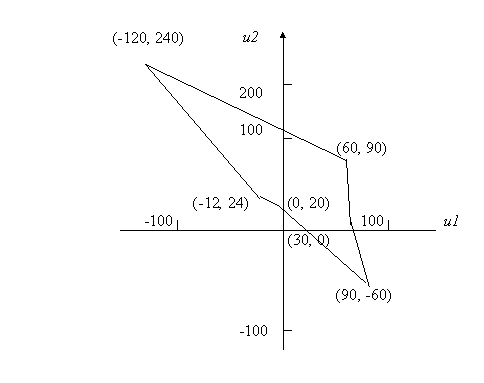
Рис. 3.2.

Для отыскания интервалов Ui, i=,применяются как прямые, так и итерационные методы. Прямые интервальные методы часто представляют собой непосредственное перенесение на интервальный случай обычных (вещественных) прямых методов. Рассмотрим их применение на примере метода Гаусса.

[К предыдущей главе].....[К содержанию] ......[К следующей главе]